目录
[(二)Stack.h 完整代码](#(二)Stack.h 完整代码)
[(二)解题思路(利用栈的 LIFO 特性)](#(二)解题思路(利用栈的 LIFO 特性))
一、栈的本质与核心特性
(一)栈的定义与本质
一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶,另一端称为栈底,完全封闭。
栈中的数据元素遵守**后进先出LIFO(Last In First Out)**的原则。
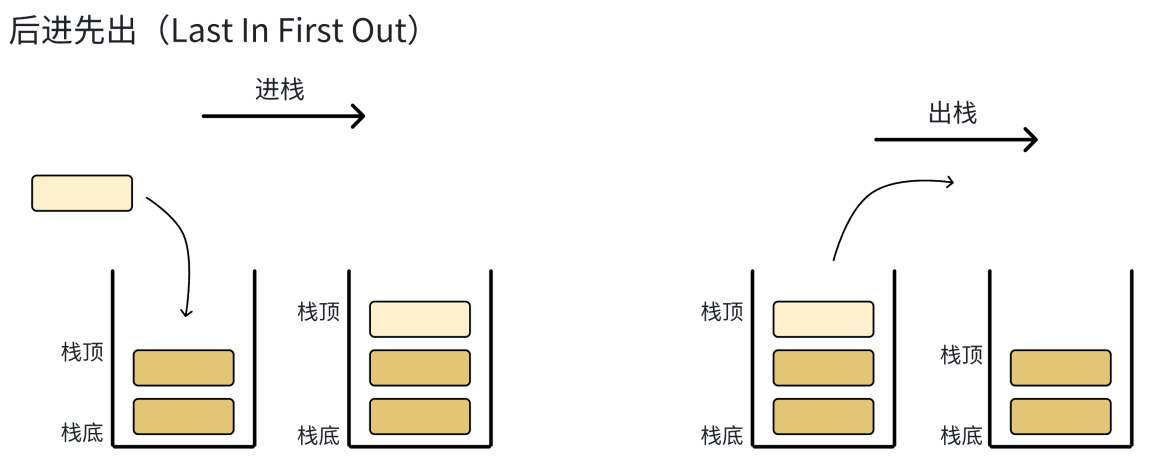
(二)核心术语
1、栈顶(Top)
允许操作的一端,用指针 / 下标标记,既表示 "下次插入位置",也隐含 "有效元素个数"
2、栈底(Bottom):固定封闭的一端,是栈的起始点,空栈时栈顶与栈底重合
**3、压栈:**栈的插入操作叫做进栈 / 压栈 / 入栈,入数据在栈顶。
**4、出栈:**栈的删除操作叫做出栈。出数据也在栈顶。
**5、空栈:**栈中无任何数据时,栈顶与栈底重合(下标均为 0),此时不可执行出栈操作。
**6、满栈:**数组实现中栈的有效元素个数等于容量(Top = Capacity),需触发扩容。
**★**从数学角度,栈可定义为一个有序集合 S,仅支持两种核心操作:
**① Push(S, x):**将元素 x 插入到集合 S 的顶端(栈顶);
**② Pop(S):**从集合 S 的顶端移除并返回元素(若 S 非空)。
(三)关于栈顶与栈底指针的指向
**1、**空栈时,栈顶 = 栈底。
**2、**有元素时,栈底指针指向栈的底部元素,栈顶指针指向下一个可入栈的位置,即当前栈顶元素的下一个地址。
**Tip:**这种设计可以通过栈顶与栈底指针的差值快速计算栈中元素个数(栈顶指针 - 栈底指针 = 元素个数),是一种常见的实现方式。
(四)逻辑与物理结构
**1、逻辑结构:**必为线性结构,数据元素间存在一对一的线性关系。
**2、物理结构:**取决于底层实现方式(数组或链表)。如果实现方式是数组,那么就是连续存储;如果实现方式是链表,那么就是非连续存储。
二、栈的底层实现方案
(一)链表实现(不太推荐)
1、设计思路与关键决策
链表实现栈的核心是将栈顶定义在链表头部,原因如下:
**(1)**链表头部插入 / 删除元素时,仅需修改指针指向,时间复杂度为 O(1);
**(2)**若栈顶定义在链表尾部,插入/删除需遍历链表找尾结点,时间复杂度升至 O(n),效率极低。
(二)数组实现(推荐方案)
1、设计思路与关键决策
数组实现栈的核心是将栈顶定义在数组尾部,原因如下:
**(1)**数组尾部插入 / 删除元素时,无需移动其他元素,时间复杂度为 O(1);
**(2)**若栈顶定义在数组头部,插入 / 删除需移动所有元素,时间复杂度升至 O(n),效率极低。
2、数据结构设计
cpp
// 栈结构定义(数组实现)
typedef int STDataType;
typedef struct Stack {
STDataType* arr; // 动态数组:存储栈元素(避免固定大小限制)
int top; // 栈顶指针:标记下次插入位置,同时等于有效元素个数
int capacity; // 容量:当前数组可容纳的最大元素个数
} ST;3、关键操作逻辑
**(1)**动态扩容机制
初始容量为 4,空间不足时按 2 倍扩容(避免初始容量为 0 时直接倍增失效)。
**(2)初始化:**数组指针置空,栈顶(top)和容量(capacity)均设为 0。
**(3)入栈:**先检查容量,不足则扩容,再将数据插入栈顶(top 位置),随后 top 自增。
**(4)出栈:**直接将 top 自减(无需物理删除元素,通过 top 标记有效数据范围)。
**(5)取栈顶元素:**返回数组下标为top - 1的元素(top 指向下次插入位置)。
(三)选择数组实现的原因
数组实现的栈,元素是连续存储的,没有额外的指针开销 ,且无内存碎片,所有空间都用于存储有效数据,因此空间效率更高。
什么是内存碎片呢?
内存碎片:当链表结点频繁插入、删除后,内存中会出现很多零散的小空间**(这些空间太小,无法存储新的大对象),这就是**内存碎片,因此链表的内存特性是 "有碎片"。
再形象一点就是,假如第一个结点与第二个结点之间,相隔了60个字节,我现在如果要存储一个80个字节空间的数据,这里就存不下,就造成了内存碎片的浪费。
即使加上后面的空间足够,但是也不行,因为这是两个独立的空闲块。
简单说:碎片不是 "空间不够",而是 "空间散了,拼不成大块"
三、环境搭建与结构体定义
(一)工程文件结构
需创建 3 个文件,分工明确,便于维护:
**1、Stack.h:**结构体定义、函数声明、头文件引入(对外提供接口)。
**2、Stack.c:**所有函数的具体实现(内部逻辑)。
**3、test.c:**测试用例编写,验证功能正确性(调用接口)。
(二)Stack.h 完整代码
cpp
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
// 栈数据类型抽象(支持后续修改)
typedef int STDataType;
// 栈结构定义
typedef struct Stack {
STDataType* arr; // 动态数组存储数据
int top; // 栈顶指针(标记下次插入位置,同时表示有效元素个数)
int capacity; // 栈的容量
} ST;
// 核心操作声明
//1、初始化与销毁
void STInit(ST* ps); // 初始化栈
void STDestroy(ST* ps); // 销毁栈
//2、辅助函数
void Print(ST* ps); // 打印栈元素(辅助操作)
bool StackEmpty(ST* ps); // 判断栈是否为空
//3、栈操作
void StackPush(ST* ps, STDataType x); // 入栈
void StackPop(ST* ps); // 出栈
STDataType StackTop(ST* ps); // 取栈顶元素
int STSize(ST* ps); // 获取有效元素个数四、核心函数的实现
(一)初始化栈
cpp
// 初始化栈
void STInit(ST* ps)
{
assert(ps); // 断言避免空指针
ps->arr = NULL; // 动态数组初始为空(未申请内存)
ps->top = 0;// 栈顶初始为0:空栈时下次插入位置为数组下标0
ps->capacity = 0; // 初始容量为0:未申请内存时容量为0
}(二)辅助函数
1、栈状态判断
cpp
// 判断栈是否为空
bool StackEmpty(ST* ps)
{
assert(ps);
return ps->top == 0; // 空栈标志:top为0则表示无有效元素
}**Tip:**这个栈状态判断主要用于出栈操作,只有栈不为空,才可以进行出栈;进行判空的断言判断是 assert(!StackEmpty(ps));
2、打印操作
cpp
void Print(ST* ps)
{
assert(ps);
for (int i = 0; i < ps->top; i++) {
printf("%d ", ps->arr[i]);
}
printf("\n");
}(三)栈操作
1、入栈
入栈需先检查容量,不足时触发动态扩容,扩容逻辑需处理 "初始容量为 0" 的特殊场景:
cpp
void StackPush(ST* ps, STDataType x)
{
assert(ps != NULL);
// 1. 检查容量:栈满(top == capacity)时扩容
if (ps->top == ps->capacity)
{
//(1)扩容:初始容量为4,后续按2倍扩容(平衡效率与空间)
int newCapacity;
if (ps->capacity == 0)
newCapacity = 4;
else
newCapacity = ps->capacity * 2;
//(2)申请新内存
STDataType* tmp = (STDataType*)realloc(ps->arr, newCapacity * sizeof(STDataType));
if (tmp == NULL)
{
perror("realloc fail: ");
exit(1);
}
//(3)更新栈的数组指针和容量【realloc可能返回新地址】
ps->arr = tmp;
ps->capacity = newCapacity;
}
// 2. 空间足够则插入元素
ps->arr[ps->top] = x;
ps->top++;
}扩容细节说明:
**(1)****初始容量设为 4:**避免频繁扩容(若初始为 1,插入 4 个元素需扩容 3 次);
**(2)****2 倍扩容:**符合 "amortized O (1)" 时间复杂度(多次插入的平均时间为 O (1));
**(3)**使用 realloc 而非 malloc:若后续空间足够,realloc 可直接复用原有内存,减少内存拷贝开销;如果不够,则再另一块内存创建,返回新地址,所以可能返回新地址。
2、出栈
cpp
void StackPop(ST* ps)
{
// 断言:栈不能为空(空栈出栈是非法操作)
assert(ps != NULL && !StackEmpty(ps));
// 仅需top自减:后续插入会覆盖原数据,无需显式删除
ps->top--;
}**关键注意:**出栈不删除物理元素是为了效率,即O(1) 时间复杂度。但需注意:若栈存储敏感数据(如密码),需手动覆盖原数据,以避免数据泄露。
3、取栈顶元素
栈顶元素存储在 top - 1 位置(因 top 指向下次插入位置):
cpp
STDataType StackTop(ST* ps)
{
// 断言:栈不能为空(空栈无栈顶元素)
assert(ps != NULL && !StackEmpty(ps));
return ps->arr[ps->top - 1]; // 返回top前一个位置的元素
}4、获取中有效元素个数
cpp
// 获取有效元素个数(直接返回top值)
int STSize(ST* ps)
{
assert(ps);
return ps->top;
}五、测试代码(test.c)
cpp
#include"Stack.h"
void test01() {
ST st;
STInit(&st); // 初始化栈
// 入栈操作:1、2、3、4
StackPush(&st, 1);
StackPush(&st, 2);
StackPush(&st, 3);
StackPush(&st, 4);
// 打印栈元素(输出:1 2 3 4)
Print(&st);
// 输出有效元素个数(输出:4)
printf("有效元素个数:%d\n", STSize(&st));
// 出栈操作(依次弹出4、3、2、1)
while (!StackEmpty(&st)) {
int top = StackTop(&st); // 取栈顶元素
printf("出栈元素:%d\n", top);
StackPop(&st);
}
STDestroy(&st); // 销毁栈
}
int main() {
test01();
return 0;
}六、栈的算法题:有效的括号
(一)题目简述
1、题目描述
给定仅包含 '('、')'、'{'、'}'、'['、']' 的字符串,判断字符串是否有效。
有效字符串需满足:① 左括号必须用相同类型的右括号闭合;②左括号必须按正确顺序闭合(后出现的左括号先闭合);③ 每个右括号必有对应的左括号。
**2、题目链接:**https://leetcode.cn/problems/valid-parentheses/description/
(二)解题思路(利用栈的 LIFO 特性)
**1、遍历字符串:**遇到左括号('('、'{'、'[')直接入栈;
2、遇到右括号时
**(1)**若栈为空(无对应左括号),直接返回无效。
**(2)**取出栈顶元素,判断是否为匹配的左括号,如 ')' 匹配 '(';不匹配则返回无效,匹配则执行出栈操作。
**3、遍历结束后:**若栈为空,即所有左括号均匹配闭合,则字符串有效;否则无效。
(三)代码实现
cpp
bool isValid(char* s)
{
// 1. 初始化栈(存储左括号)
ST st;
STInit(&st);
char* p = s; // 指针遍历字符串
// 2. 遍历字符串
// 循环终止条件:遍历到字符串结束符('\0')
while (*p != '\0')
{
if (*p == '(' || *p == '{' || *p == '[') {
StackPush(&st, *p);//左括号入栈
}
else {
// 右括号处理:栈空则无效
if (StackEmpty(&st)) {
STDestroy(&st); // 销毁栈(避免内存泄漏)
return false;
}
// 取栈顶元素匹配
char topChar = StackTop(&st);
// 取栈顶元素匹配
char top = StackTop(&st);
if ((top == '(' && *p != ')') ||
(top == '{' && *p != '}') ||
(top == '[' && *p != ']')) {
STDestroy(&st);
return false;
}
StackPop(&st); // 匹配成功,出栈
}
p++; // 指针移动到下一个字符
}
// 3. 遍历结束:检查栈是否为空(即是否存在未闭合左括号)
bool ret;
if (StackEmpty(&st))
ret = true;
else
ret = false;
STDestroy(&st); // 销毁栈(必须执行,避免内存泄漏)
return ret;
}**Tip:**代码中用到的 StackEmpty(&st) 等栈操作函数,前文已完成实现。答题时,只需将这些函数复制到当前代码中,即可直接调用,无需重复编写。
(四)边界场景处理
**1、**字符串以右括号开头(栈空直接返回无效);
**2、**左右括号类型不匹配【 如 :(] 】;
**3、**单侧括号(仅左括号或仅右括号)。
**4、**遍历结束后栈非空【左括号未完全闭合,如 :'(' 】;