CG 方法(共轭梯度)的数学推导及其算法
- Gram-Schmidt 正交化本质是 Q R QR QR 分解, Q Q Q 是正交基, R R R 是原向量组在正交基上的投影。
- Krylov 子空间,边产生 A ∗ v j A*v_j A∗vj,边做正交化,形成 Krylov 子空间一组正交基,这个过程叫 Arnoldi 过程。
- Arnoldi 过程中,如果 A A A 是实对称,算法流程某些变量相等了,此过程操作可以简化,称为 Lanczos 过程。
- Lanczos 过程中(取 v 1 = r 0 v_1 = r_0 v1=r0),寻求 Krylov 子空间中 A A A 范数意义下的最佳逼近解,可以得到 Lanczos 算法。
- Lanczos 算法中,三对角方程组的求解步骤通过 L U LU LU 分解待定系数法,得到的迭代关系式融入到 Lanczos 迭代过程中,为 D-Lanczos 算法。
- D-Lanczos 算法推导过程中,引入了共轭方向组 p i p_i pi 及其性质,和残差向量 r m r_m rm 的性质,取当前步解为前一步解和共轭方向的线性组合,可得共轭梯度算法。这里利用到残差向量的正交性,共轭方向的 A A A 共轭性。
文章目录
-
- [CG 方法(共轭梯度)的数学推导及其算法](#CG 方法(共轭梯度)的数学推导及其算法)
-
- [Gram-Schmidt 正交化](#Gram-Schmidt 正交化)
- [Krylov 子空间正交基构造](#Krylov 子空间正交基构造)
- 正交投影与方程组求解
- 共轭梯度(CG)算法
CG 算法的推导方法很多,其中一种比较容易的以终为始的推导可参考:
https://blog.csdn.net/lusongno1/article/details/124988357
这里采用 Yousef Saad 的 Iterative Methods for Sparse Linear Systems 里面提到的,通过 Lanczos 算法进行过渡和推导的一种方式。
Gram-Schmidt 正交化
下面是高等线性代数里标准的 Gram-Schmidt 正交化过程:

其中, r i j r_{ij} rij 是第 j j j 个向量在已正交化空间的投影向量系数, x i x_i xi 是原向量, q i q_i qi 是正交化后的向量。
考虑舍入误差的情况,有如下改进版本的 Gram-Schmidt 算法:

Krylov 子空间正交基构造
对于 Krylov 子空间,
K m ( A , r ( 0 ) ) = span { r ( 0 ) , A r ( 0 ) , ⋯ , A m − 1 r ( 0 ) } \mathcal{K}_m\left(A, r^{(0)}\right)=\operatorname{span}\left\{r^{(0)}, A r^{(0)}, \cdots, A^{m-1} r^{(0)}\right\} Km(A,r(0))=span{r(0),Ar(0),⋯,Am−1r(0)}
自然的基底并不是正交的,我们可以通过 Gram-Schmidt 过程,结合 Krylov 子空间的概念,生成一组正交基,这个过程叫 Arnoldi 过程,核心算法流程如下:

事实上,容易证明,上述 Arnoldi 过程,得到了 Krylov 子空间 K m ( A , v 1 ) \mathcal{K}_m\left(A, v_1\right) Km(A,v1) 的一组正交基。它是对一般矩阵的到 Krylov 子空间上的正交投影方法。
h i j h_{ij} hij 表示的是向量 w j = A v j w_j = Av_j wj=Avj 在 v j v_j vj 上的投影内积。
我们用 V m V_m Vm 表示以 v 1 , ⋯ , v m v_1, \cdots, v_m v1,⋯,vm 为列的 n × m n \times m n×m 矩阵, H ˉ m \bar{H}m Hˉm 表示元素为 h i j h{i j} hij 的 ( m + 1 ) × m (m+1) \times m (m+1)×m 的上 Hessenberg 矩阵, H m H_m Hm 表示在 H ˉ m \bar{H}_m Hˉm 中删去最后一行所得的矩阵。
由
A v j = ∑ i = 1 j + 1 h i j v i , j = 1 , 2 , ⋯ , m . A v_j=\sum_{i=1}^{j+1} h_{i j} v_i, \quad j=1,2, \cdots, m . Avj=i=1∑j+1hijvi,j=1,2,⋯,m.
写成矩阵形式,实际上是
A V m = V m H m + h m + 1 , m v m + 1 e m ⊤ A V_m=V_m H_m+h_{m+1, m} v_{m+1} e_m^{\top} AVm=VmHm+hm+1,mvm+1em⊤
左乘 V m T V_m^T VmT,可以推导得到如下关系:
V m T A V m = H m . V_m^{\mathrm{T}} A V_m=H_m . VmTAVm=Hm.
容易证明,如果 A A A 是实对称矩阵,那么 H m H_m Hm 一定是对称三对角的(三对角情况后面用 T m Tm Tm)那么,上述 Arnoldi 过程就可以约化为 Lanczos过程

正交投影与方程组求解
对于线性方程组
A x = b , A ∈ R n × n , x , b ∈ R n A x=b, \quad A \in \mathbb{R}^{n \times n}, x, b \in \mathbb{R}^n Ax=b,A∈Rn×n,x,b∈Rn
取 r i = b − A x i r_i = b-Ax_i ri=b−Axi。
在 Arnoldi 过程中,取 v 1 = r 0 / ∥ r 0 ∥ 2 v_1=r_0 /\left\|r_0\right\|_2 v1=r0/∥r0∥2,令 β = ∥ r 0 ∥ 2 \beta=\left\|r_0\right\|_2 β=∥r0∥2。
欲求 Krylov 正交空间中 A A A 范数意义下的最佳逼近,根据定理:
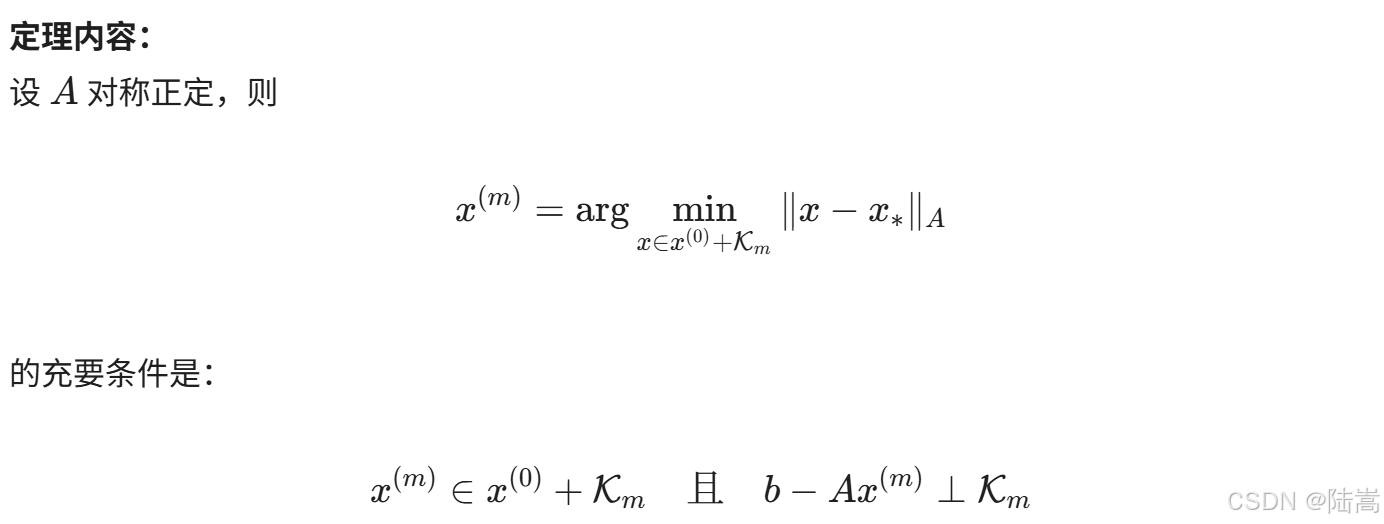
考虑 x m = x 0 + V m y m x_{m}=x_{0}+V_m y_{m} xm=x0+Vmym,
那么,由上述定理,
0 = V m ⊤ ( b − A x m ) = V m ⊤ ( r 0 − A V m y m ) = V m ⊤ ( β v 1 ) − V m ⊤ A V m y m = β e 1 − T m y m . 0=V_m^{\top}\left(b-A x_{m}\right)=V_m^{\top}\left(r_0-A V_m y_{m}\right)=V_m^{\top}\left(\beta v_1\right)-V_m^{\top} A V_m y_{m}=\beta e_1-T_m y_{m} . 0=Vm⊤(b−Axm)=Vm⊤(r0−AVmym)=Vm⊤(βv1)−Vm⊤AVmym=βe1−Tmym.
那么正交投影空间近似解可由如下方式给出:
x m = x 0 + V m y m , y m = T m − 1 ( β e 1 ) . x_m=x_0+V_m y_m, \quad y_m=T_m^{-1}\left(\beta e_1\right) . xm=x0+Vmym,ym=Tm−1(βe1).
从而有 Lanczos 算法:

Lanczos 算法中的关键是需要求 T m − 1 T_m^{-1} Tm−1。
由 A V m = V m H m + h m + 1 , m v m + 1 e m ⊤ A V_m=V_m H_m+h_{m+1, m} v_{m+1} e_m^{\top} AVm=VmHm+hm+1,mvm+1em⊤,直接可得:
b − A x m = − β m + 1 e m T y m v m + 1 b-A x_m=-\beta_{m+1} e_m^T y_m v_{m+1} b−Axm=−βm+1emTymvm+1
由此可见残差向量 b − A x m b-Ax_m b−Axm 事实上,不仅垂直 K m \mathcal{K}m Km,还是在 v m + 1 v{m+1} vm+1 的方向上。
考虑 T m T_m Tm 的 LU 分解, T m = L m U m T_m=L_m U_m Tm=LmUm,即
T m = ( 1 λ 2 1 λ 3 1 λ 4 1 λ 5 1 ) ( η 1 β 2 η 2 β 3 η 3 β 4 η 4 β 5 η 5 ) . T_m=\left(\begin{array}{ccccc} 1 & & & & \\ \lambda_2 & 1 & & & \\ & \lambda_3 & 1 & & \\ & & \lambda_4 & 1 & \\ & & & \lambda_5 & 1 \end{array}\right)\left(\begin{array}{ccccc} \eta_1 & \beta_2 & & & \\ & \eta_2 & \beta_3 & & \\ & & \eta_3 & \beta_4 & \\ & & & \eta_4 & \beta_5 \\ & & & & \eta_5 \end{array}\right) . Tm= 1λ21λ31λ41λ51 η1β2η2β3η3β4η4β5η5 .
注意,这里的 β m \beta_m βm 固定为了 Lanczos 算法中 β m \beta_m βm。
那么,根据最佳逼近表达,解为
x m = x 0 + V m U m − 1 L m − 1 ( β e 1 ) . x_m=x_0+V_m U_m^{-1} L_m^{-1}\left(\beta e_1\right) . xm=x0+VmUm−1Lm−1(βe1).
假设
P m ≡ V m U m − 1 , z m = L m − 1 β e 1 , P_m \equiv V_m U_m^{-1}, \quad z_m=L_m^{-1} \beta e_1, Pm≡VmUm−1,zm=Lm−1βe1,
那么,有
x m = x 0 + P m z m x_m=x_0+P_m z_m xm=x0+Pmzm
用 p m p_m pm 表示 P m P_m Pm 的第 m m m 列,用 ζ m \zeta_m ζm 表示向量 z m z_m zm 的第 m m m 个元素。
通过待定系数法,可以得到解的递推式,将这个地推过程耦合到 Lanczos 正交化过程中,就得到了 Lanczos 算法的直接形式,如下:

共轭梯度(CG)算法
由上述 Lanczos 算法推导过程,实际上引出 p i p_i pi 这个量。容易证明, r m r_m rm 和 p i p_i pi 满足:
(1)每个残差向量 r m r_m rm 使得 r m = σ m v m + 1 r_m=\sigma_m v_{m+1} rm=σmvm+1 ,其中 σ m \sigma_m σm 为某个标量,从而残差向量是两两正交的;
(2)辅助向量 p i p_i pi 形成一个 A A A 共轭集合,即对 i ≠ j , ( A p i , p j ) = 0 i \neq j,\left(A p_i, p_j\right)=0 i=j,(Api,pj)=0 .
利用这些量及其性质,我们可以推导 CG 算法:
不妨取当前步的解为前一步的解和共轭方向的线性组合,
x j + 1 = x j + α j p j x_{j+1}=x_j+\alpha_j p_j xj+1=xj+αjpj
易证明
α j = ( r j , r j ) ( A p j , r j ) . \alpha_j=\frac{\left(r_j, r_j\right)}{\left(A p_j, r_j\right)} . αj=(Apj,rj)(rj,rj).
r j + 1 = r j − α j A p j r_{j+1}=r_j-\alpha_j A p_j rj+1=rj−αjApj
β j = − ( r j + 1 , A p j ) ( p j , A p j ) = ( r j + 1 , r j + 1 ) ( r j , r j ) . \beta_j=-\frac{\left(r_{j+1}, A p_j\right)}{\left(p_j, A p_j\right)}=\frac{\left(r_{j+1}, r_{j+1}\right)}{\left(r_j, r_j\right)} . βj=−(pj,Apj)(rj+1,Apj)=(rj,rj)(rj+1,rj+1).
p j + 1 = r j + 1 + β j p j p_{j+1}=r_{j+1}+\beta_j p_j pj+1=rj+1+βjpj
由此,便得到如下的共轭梯度算法:

其 MATLAB 例程如下:
clc
clear
sz = 10;
A0 = randn(sz);
A = A0'*A0;
b = ones(size(A,1),1);
x0 = ones(size(A,1),1);
[x, iter] = cg(A,b,x0);
xt = A\b;
err = norm(x-xt)
function [x, iter] = cg(A,b,x0,tol, maxit)
arguments
A double
b double
x0 double
tol double = 1e-7 % 默认参数值
maxit double = 10000 % 默认值为空,下面会处理
end
r = b - A*x0;
p = r;
x = x0;
iter = 0;
while (norm(r) > tol || iter > maxit)
iter = iter + 1;
alpha = r'*r/(p'*A*p);
x = x + alpha*p;
r1 = r - alpha*A*p;
beta = (r1'*r1)/(r'*r);
p = r1+beta*p;
r = r1;
end
endCG 算法的每个迭代步的主要运算为一个矩阵向量乘积和两个向量内积。