机器学习与模式识别——SVM

一．实验目的

• 熟悉SVM基本概念。
• 了解SVM对偶函数。
• 熟悉SMO模型。

二．实验内容

1.上机实验题一

实现书中图6.7基于支持向量机算法的山鸢尾识别问题。

2.上机实验题二

利用图6.12中带核函数的SMO算法求解变色鸢尾识别问题，实现图6.15。

3.上机实验题三

采用软间隔支持向量机算法求解弗吉尼亚鸢尾识别问题。实现图6.18

4.上机实验四 国际政治家面部识别。

在Sklearn的数据库中集成了一组由7位国际政治家 Ariel Sharon，Colin Powell，Donald Rumsfeld，George Bush，Gerhard Schroder，Hugo Chavez 和 Tony Blair 的面部组成的图片集。图6.21是4幅图片采样,从左到右分别为 Gerhard Schroder，George Bush，Colin Powell和Tony Blair。

在Sklearn数据集中有1288条数据。每条数据的特征组是一个1850维的向量。数据表示的是一个50×37的图片像素灰度矩阵。标签是一 个0~6的整数，分别表示7位政治家。

图6.22是获取与观察数据的程序。第2行导入获取数据的函数fetch_lfw_people。第5行调用该函数读取数据。第6行打印target_names,从而可以获得标签与人名的对应关系，例如标签3对应George Bush。第7、8行分别获取特征与标签。第10~12行打印出一张图片。

基于这一数据集，请对每一位政治家完成如下任务：给定一张图片，预测图片中的人物是否为这位政治家。

三．实验要求

1.结合上课内容，写出程序，并调试程序，要给出测试数据和实验结果。

2.整理上机步骤，总结经验和体会。

3.完成实验报告和上交源程序

四 ．实验 内容

1 . 上机实验题一

利用支持向量机（SVM）算法对鸢尾花数据集进行二分类。首先，从sklearn库中导入了鸢尾花数据集，并从中提取了前两个特征作为输入特征X。接着，将目标变量y进行了转换，仅保留类别0的数据，并将它们标记为-1，其他类别标记为1。然后，使用train_test_split函数将数据集分为训练集和测试集，测试集占总数据的40%。

接下来，初始化了一个SVM模型，并使用训练集对其进行训练，其中设置了迭代次数上限为10。训练完成后，定义了一个绘图函数plot_figure，该函数用于可视化SVM的决策边界。这个函数计算了决策边界的方程，并在图上绘制了两个类别的数据点以及决策边界。最后，分别对训练集和测试集调用了绘图函数，以展示模型在这两个数据集上的表现。

（1）定义SVM算法

import numpy as np

class SVM:
    def get_H(self, Lambda, i, j, y):
        if y[i]==y[j]:
            return Lambda[i] + Lambda[j]
        else:
            return float("inf")
    
    def get_L(self, Lambda, i, j, y):
        if y[i]==y[j]:
            return 0.0
        else:
            return max(0, Lambda[j] - Lambda[i])
            
    def smo(self, X, y, K, N):
        m, n = X.shape
        Lambda = np.zeros((m,1))
        epsilon = 1e-6
        for t in range(N):
            for i in range(m):
                for j in range(m):
                    D_ij = 2 * K[i][j] - K[i][i] - K[j][j]
                    if abs(D_ij) < epsilon:
                        continue
                    E_i = K[:, i].dot(Lambda * y) - y[i]
                    E_j = K[:, j].dot(Lambda * y) - y[j]
                    delta_j = 1.0 * y[j] * (E_j - E_i) / D_ij
                    H_ij = self.get_H(Lambda, i, j, y)
                    L_ij = self.get_L(Lambda, i, j, y)
                    if Lambda[j] + delta_j > H_ij:
                        delta_j = H_ij - Lambda[j]
                        Lambda[j] = H_ij
                    elif Lambda[j] + delta_j < L_ij:
                        delta_j = L_ij - Lambda[j]
                        Lambda[j] = L_ij
                    else:
                        Lambda[j] += delta_j
                    delta_i = - y[i] * y[j] * delta_j
                    Lambda[i] += delta_i                 
                    if Lambda[i] > epsilon:
                        b = y[i] - K[:, i].dot(Lambda * y)
                    elif Lambda[j] > epsilon:
                        b = y[j] - K[:, j].dot(Lambda * y)
        self.Lambda = Lambda
        self.b = b
        
    def fit(self, X, y, N = 10):
        K = X.dot(X.T)
        self.smo(X, y, K, N)
        self.w = X.T.dot(self.Lambda * y)
        
    def predict(self, X):
        return np.sign(X.dot(self.w) + self.b)

（2）基于支持向量机算法的山鸢尾识别问题

import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
from support_vector_machine.lib.svm_smo import SVM

def plot_figure(X, y, model):
    z = np.linspace(4, 8, 200)
    w = model.w
    b = model.b
    L = - w[0] / w[1] * z - b / w[1]
    plt.plot(X[:, 0][y[:, 0]==1], X[:, 1][y[:, 0]==1], "bs",  ms=3)
    plt.plot(X[:, 0][y[:, 0]==-1], X[:, 1][y[:, 0]==-1], "yo",  ms=3)
    plt.plot(z, L)
    plt.show()

iris = datasets.load_iris()
X= iris["data"][:, (0,1)]
y = 2 * (iris["target"]==0).astype(np.int32).reshape(-1,1) - 1
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=5)

model = SVM()
model.fit(X_train, y_train, N=10)
plot_figure(X_train, y_train, model)
plot_figure(X_test, y_test, model)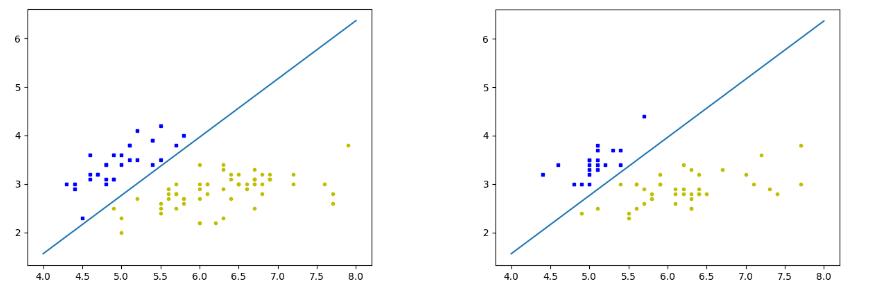

2.上机实验题二

使用序列最小优化（SMO）算法来训练支持向量机（SVM）的过程，并且扩展到了核SVM，以处理非线性可分的数据。首先，定义了一个SVM类，该类包含了SMO算法的核心逻辑。SMO算法通过迭代优化两个变量的拉格朗日乘子（Lambda）来最小化目标函数，同时保持KKT条件。算法中使用了启发式方法选择拉格朗日乘子对进行优化，并更新对应的乘子值和偏置项b。

接着，定义了一个核SVM类，它继承自SVM类，并添加了核函数的支持。核SVM类通过一个核函数来计算数据点之间的相似度，而不是直接在特征空间中计算。这样可以处理原始特征空间中线性不可分的数据。核SVM类中的fit方法首先计算核矩阵，然后调用父类的SMO方法来训练模型。

最后，提供了一个使用径向基函数（RBF）核的核SVM模型，用于鸢尾花数据集的分类。模型首先加载鸢尾花数据集，然后提取特定的特征，并将其分为训练集和测试集。模型使用RBF核函数来计算核矩阵，并在训练集上训练。训练完成后，模型预测了一个网格上所有点的类别，并使用等高线图来可视化决策边界，显示了不同类别的区域。

（1）定义SVM算法

import numpy as np

class SVM:
    def get_H(self, Lambda, i, j, y):
        if y[i]==y[j]:
            return Lambda[i] + Lambda[j]
        else:
            return float("inf")
    
    def get_L(self, Lambda, i, j, y):
        if y[i]==y[j]:
            return 0.0
        else:
            return max(0, Lambda[j] - Lambda[i])
            
    def smo(self, X, y, K, N):
        m, n = X.shape
        Lambda = np.zeros((m,1))
        epsilon = 1e-6
        for t in range(N):
            for i in range(m):
                for j in range(m):
                    D_ij = 2 * K[i][j] - K[i][i] - K[j][j]
                    if abs(D_ij) < epsilon:
                        continue
                    E_i = K[:, i].dot(Lambda * y) - y[i]
                    E_j = K[:, j].dot(Lambda * y) - y[j]
                    delta_j = 1.0 * y[j] * (E_j - E_i) / D_ij
                    H_ij = self.get_H(Lambda, i, j, y)
                    L_ij = self.get_L(Lambda, i, j, y)
                    if Lambda[j] + delta_j > H_ij:
                        delta_j = H_ij - Lambda[j]
                        Lambda[j] = H_ij
                    elif Lambda[j] + delta_j < L_ij:
                        delta_j = L_ij - Lambda[j]
                        Lambda[j] = L_ij
                    else:
                        Lambda[j] += delta_j
                    delta_i = - y[i] * y[j] * delta_j
                    Lambda[i] += delta_i                 
                    if Lambda[i] > epsilon:
                        b = y[i] - K[:, i].dot(Lambda * y)
                    elif Lambda[j] > epsilon:
                        b = y[j] - K[:, j].dot(Lambda * y)
        self.Lambda = Lambda
        self.b = b
        
    def fit(self, X, y, N = 10):
        K = X.dot(X.T)
        self.smo(X, y, K, N)
        self.w = X.T.dot(self.Lambda * y)
        
    def predict(self, X):
        return np.sign(X.dot(self.w) + self.b)

（2）定义带核函数的SMO算法

import numpy as np
from support_vector_machine.lib.svm_smo import SVM

class KernelSVM(SVM):         
    def __init__(self, kernel = None):
        self.kernel = kernel
    
    def get_K(self, X_1, X_2):
        if self.kernel == None:
            return X_1.dot(X_2.T) 
        m1, m2 = len(X_1), len(X_2)
        K = np.zeros((m1, m2))
        for i in range(m1):
            for j in range(m2):
                K[i][j] = self.kernel(X_1[i], X_2[j])
        return K
        
    def fit(self, X, y, N=10):
        K = self.get_K(X, X) 
        self.smo(X, y, K, N)
        self.X_train = X
        self.y_train = y
         
    def predict(self, X):
        K = self.get_K(X, self.X_train)
        return np.sign(K.dot(self.Lambda * self.y_train) + self.b)

（3）带核函数的SMO算法求解变色鸢尾识别问题

import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
from support_vector_machine.lib.kernel_svm import KernelSVM

def rbf_kernel(x1, x2):
    sigma = 1.0
    return np.exp(-np.linalg.norm(x1 - x2, 2) ** 2 / sigma)
    
iris = datasets.load_iris()
X= iris["data"][:,(2,3)]
y = 2 * (iris["target"]==1).astype(np.int32).reshape(-1,1) - 1
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=5)
model = KernelSVM(kernel = rbf_kernel)
model.fit(X_train, y_train)

x0s = np.linspace(1, 7, 100)
x1s = np.linspace(0, 3, 100)
x0, x1 = np.meshgrid(x0s, x1s)
W = np.c_[x0.ravel(), x1.ravel()]
u= model.predict(W).reshape(x0.shape)
plt.plot(X_train[:, 0][y_train[:,0]==1] , X_train[:, 1][y_train[:,0]==1], "bs")
plt.plot(X_train[:, 0][y_train[:,0]==-1], X_train[:, 1][y_train[:,0]==-1], "yo")
plt.contourf(x0, x1, u, alpha=0.2)
plt.show()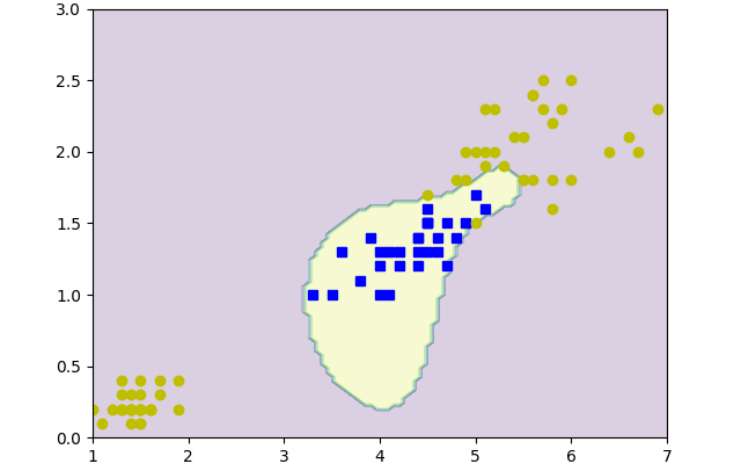

3.上机实验题三

实现了一个软间隔支持向量机（Soft SVM）分类器，用于处理可能不完全线性可分的数据集。软间隔SVM通过引入正则化参数C，允许一些数据点位于间隔边界之外，从而在模型复杂度和训练误差之间取得平衡。分类器的核心是SMO（序列最小优化）算法，它通过迭代选择两个拉格朗日乘子进行优化，以最大化步长并更新模型参数。

在Soft SVM的实现中，get_H和get_L方法被调整以适应软间隔的约束条件，这些条件允许拉格朗日乘子在一定范围内取值，而不是硬间隔SVM中的0或无穷大。这样，即使数据集中存在一些噪声或异常值，模型也能保持较好的泛化能力。

鸢尾花数据集中的数据被分为训练集和测试集。模型在训练集上进行训练，并在测试集上进行评估，以计算其准确率。结果显示，该软间隔SVM模型在测试集上的准确率达到了95%，这表明模型能够有效地从数据中学习并进行准确的分类。此外，还运用可视化工具，用于绘制训练数据的决策边界，帮助用户直观地理解模型的分类效果。

（1）定义SVM算法

import numpy as np

class SVM:
    def get_H(self, Lambda, i, j, y):
        if y[i]==y[j]:
            return Lambda[i] + Lambda[j]
        else:
            return float("inf")
    
    def get_L(self, Lambda, i, j, y):
        if y[i]==y[j]:
            return 0.0
        else:
            return max(0, Lambda[j] - Lambda[i])
            
    def smo(self, X, y, K, N):
        m, n = X.shape
        Lambda = np.zeros((m,1))
        epsilon = 1e-6
        for t in range(N):
            for i in range(m):
                for j in range(m):
                    D_ij = 2 * K[i][j] - K[i][i] - K[j][j]
                    if abs(D_ij) < epsilon:
                        continue
                    E_i = K[:, i].dot(Lambda * y) - y[i]
                    E_j = K[:, j].dot(Lambda * y) - y[j]
                    delta_j = 1.0 * y[j] * (E_j - E_i) / D_ij
                    H_ij = self.get_H(Lambda, i, j, y)
                    L_ij = self.get_L(Lambda, i, j, y)
                    if Lambda[j] + delta_j > H_ij:
                        delta_j = H_ij - Lambda[j]
                        Lambda[j] = H_ij
                    elif Lambda[j] + delta_j < L_ij:
                        delta_j = L_ij - Lambda[j]
                        Lambda[j] = L_ij
                    else:
                        Lambda[j] += delta_j
                    delta_i = - y[i] * y[j] * delta_j
                    Lambda[i] += delta_i                 
                    if Lambda[i] > epsilon:
                        b = y[i] - K[:, i].dot(Lambda * y)
                    elif Lambda[j] > epsilon:
                        b = y[j] - K[:, j].dot(Lambda * y)
        self.Lambda = Lambda
        self.b = b
        
    def fit(self, X, y, N = 10):
        K = X.dot(X.T)
        self.smo(X, y, K, N)
        self.w = X.T.dot(self.Lambda * y)
        
    def predict(self, X):
        return np.sign(X.dot(self.w) + self.b)

（2）定义软间隔支持向量机

from support_vector_machine.lib.svm_smo import SVM

class SoftSVM(SVM):
    def __init__(self, C = 1000):
        self.C = C
    
    def get_H(self, Lambda, i,j, y):
        C = self.C
        if y[i]==y[j]:
            return min(C, Lambda[i] + Lambda[j])
        else:
            return min(C, C + Lambda[j] - Lambda[i]) 
    
    def get_L(self, Lambda, i, j, y):
        if y[i]==y[j]:
            return max(0, Lambda[i] + Lambda[j] - self.C)
        else:
            return max(0, Lambda[j] - Lambda[i])

（3）软间隔支持向量机算法求解弗吉尼亚鸢尾识别问题

from support_vector_machine.lib.svm_smo import SVM

class SoftSVM(SVM):
    def __init__(self, C = 1000):
        self.C = C
    
    def get_H(self, Lambda, i,j, y):
        C = self.C
        if y[i]==y[j]:
            return min(C, Lambda[i] + Lambda[j])
        else:
            return min(C, C + Lambda[j] - Lambda[i]) 
    
    def get_L(self, Lambda, i, j, y):
        if y[i]==y[j]:
            return max(0, Lambda[i] + Lambda[j] - self.C)
        else:
            return max(0, Lambda[j] - Lambda[i])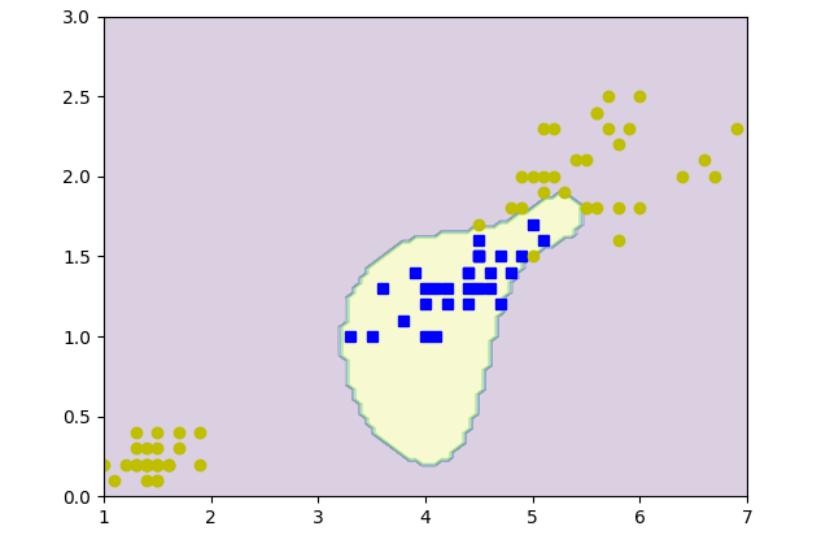

4.上机实验四 国际政治家面部识别

从一个本地数据集中识别特定政治家的面部图像。首先，定义了一个函数load_lfw_data，用于从指定的文件夹路径中加载图像数据。这个函数遍历文件夹中的每个子文件夹（代表不同的政治家），并加载其中的.jpg图像文件。每个图像被转换为灰度格式并调整到指定的大小，然后被转换为一维数组并存储在列表中。同时，每个图像的标签（即政治家的索引）也被存储在另一个列表中。

加载完数据后，打印出所有可用的政治家姓名，以确认数据集中包含的个体。接着，允许用户指定一个感兴趣的政治家姓名，然后检查这个姓名是否在数据集中。如果存在，代码会找到对应的索引，并使用这个索引来创建二元标签，即判断图像是否属于该政治家。

接下来，将数据集划分为训练集和测试集，并使用训练集来训练一个支持向量机（SVM）模型。这个模型通过一个管道（pipeline）来实现，其中包括一个标准化步骤来归一化数据，以及一个线性核的SVM分类器。模型训练完成后，使用测试集进行预测，并计算准确率。

最后，显示测试集中第一张图像的预测结果，如果预测正确，则显示该政治家的姓名；否则，显示"Other person"。整个过程的目的是验证模型是否能够准确地识别特定政治家的面部图像，并且从输出结果来看，模型在测试集上达到了100%的准确率。

import numpy as np
import os
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import make_pipeline
import matplotlib.pyplot as plt
from PIL import Image

# 本地数据集路径
data_dir = r"C:\Users\dell\Desktop\lfw_funneled"

# 手动加载数据：读取图片并转换为灰度图像，调整大小
def load_lfw_data(data_dir):
    images = []
    labels = []
    target_names = os.listdir(data_dir)  # 文件夹名为人名标签

    for label_idx, target_name in enumerate(target_names):
        target_dir = os.path.join(data_dir, target_name)
        if os.path.isdir(target_dir):  # 确保是文件夹
            for img_name in os.listdir(target_dir):
                if img_name.lower().endswith('.jpg'):  # 只读取 jpg 文件
                    img_path = os.path.join(target_dir, img_name)
                    try:
                        img = Image.open(img_path).convert('L')  # 转为灰度图像
                        img = img.resize((50, 37))  # 调整图像大小（根据需要调整）
                        img_array = np.array(img).flatten()  # 将图像展开为一维数组
                        images.append(img_array)
                        labels.append(label_idx)
                    except Exception as e:
                        print(f"Error loading image {img_name}: {e}")
    return np.array(images), np.array(labels), target_names

# 加载本地数据集
X, y, target_names = load_lfw_data(data_dir)

# 打印所有的 target_names 查看是否包含指定的政治家
print("Available target names:", target_names)

# 选择特定政治家的姓名
politician_name = "Zydrunas_Ilgauskas"  # 请替换为你感兴趣的名字（使用与数据集一致的格式）

# 检查是否存在指定的政治家，并找出其索引
if politician_name in target_names:
    # 使用 np.where 找到该政治家的索引
    politician_id = np.where(np.array(target_names) == politician_name)[0][0]
else:
    print(f"{politician_name} not found in the target names.")
    politician_id = None

if politician_id is not None:
    # 划分数据集
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

    # 创建训练和测试的标签：是特定政治家则为True，否则为False
    y_train_politician = (y_train == politician_id)
    y_test_politician = (y_test == politician_id)

    # 创建并训练分类模型
    model = make_pipeline(StandardScaler(), SVC(kernel='linear', random_state=42))
    model.fit(X_train, y_train_politician)

    # 预测特定政治家
    y_pred = model.predict(X_test)
    accuracy = accuracy_score(y_test_politician, y_pred)
    print(f"Accuracy for predicting {politician_name}: {accuracy:.4f}")

    # 预测并显示单张图片
    plt.imshow(X_test[0].reshape(37, 50), cmap='gray')  # 显示测试集中的第一张图片
    plt.title(f"Predicted: {politician_name if model.predict([X_test[0]]) else 'Other person'}")
    plt.show()