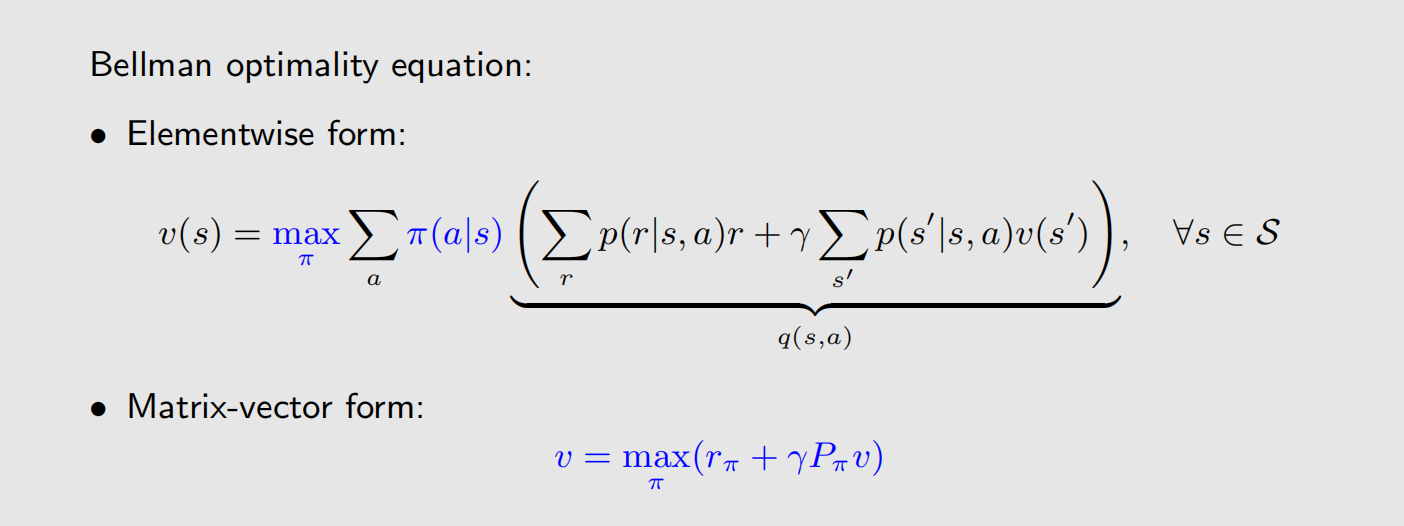贝尔曼最优公式
- [1 策略比较与最优策略](#1 策略比较与最优策略)
-
- [1.1 Action value 的作用](#1.1 Action value 的作用)
- [1.2 策略比较与最优策略](#1.2 策略比较与最优策略)
- [2 贝尔曼最优公式(Bellman Optimality Equation)](#2 贝尔曼最优公式(Bellman Optimality Equation))
-
- [2.1 贝尔曼最优公式](#2.1 贝尔曼最优公式)
- [2.2 贝尔曼最优公式求解](#2.2 贝尔曼最优公式求解)
- [3 矩阵形式的解](#3 矩阵形式的解)
-
- [3.1 收缩映射定理(Constraction Mapping theorem)](#3.1 收缩映射定理(Constraction Mapping theorem))
- [3.2 解贝尔曼最优公式](#3.2 解贝尔曼最优公式)
- [3.3 贝尔曼最优公式解的最优性](#3.3 贝尔曼最优公式解的最优性)
- [4 最优策略的有趣性质](#4 最优策略的有趣性质)
-
- [4.1 影响最优策略的因素](#4.1 影响最优策略的因素)
- [4.2 改变折扣率](#4.2 改变折扣率)
- [4.3 改变奖励机制](#4.3 改变奖励机制)
- [5 总结](#5 总结)
1 策略比较与最优策略
1.1 Action value 的作用
在网格世界中,有以下策略,根据贝尔曼公式可以得到 state value。

得到 state value 后,可以计算得到 action value:
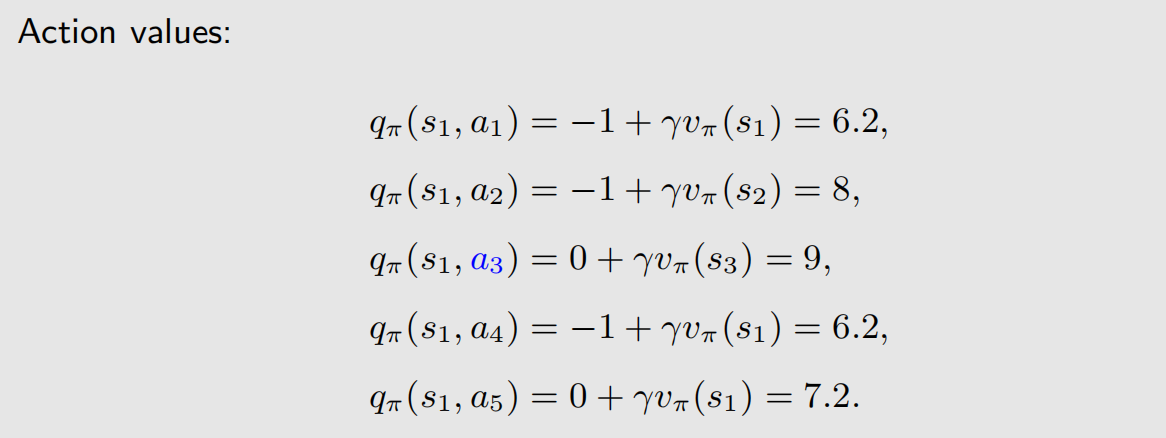
可以看到,当前状态下( S = s 1 S=s_1 S=s1), A = a 3 A=a_3 A=a3 的 action value 最高,也就是说, a 3 a_3 a3 的价值最高,但给的策略却是向右,即 A = a 2 A=a_2 A=a2,我们需要调整策略,选择最优动作。

从上面的示例可以看到,action value 可以用来调整策略。
1.2 策略比较与最优策略
如何从数学角度比较两个策略的好坏?我们上一讲介绍的 state value 就可以,如果策略A,在任何状态下,它的 state value 都高于另一个策略B,那么就说明策略A好于策略B,数学定义如下:
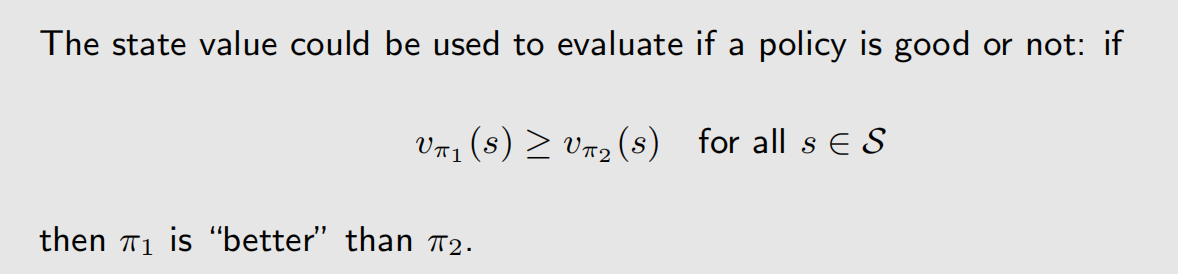
上一讲中介绍到,状态价值函数 υ π ( s ) \upsilon _{\pi}(s) υπ(s) 是状态 s s s 和策略 π \pi π 的函数,上面对比中,是遍历了所有状态,那么计算两个策略大的状态价值函数时,自变量只有策略 π \pi π 不一样。
如果一个策略好于其他所有策略,那么这个策略就是最优策略,数学定义如下:

2 贝尔曼最优公式(Bellman Optimality Equation)
2.1 贝尔曼最优公式
我们先给出贝尔曼最优公式(Bellman Optimality Equation,BOE)的定义:

贝尔曼最优公式的矩阵向量形式为:

如何理解上述公式?对于状态 s 1 s_1 s1,遍历所有策略,然后找到最大的 state value,这个最大的 state value 就是 υ ( s 1 ) \upsilon(s_1) υ(s1),其他状态以此类推。
可能有人会问,假如状态 s 1 s_1 s1 在 π 1 \pi_1 π1 时取得最大的 state value,状态 s 2 s_2 s2 在 π 2 \pi_2 π2 时取得最大的 state value,那么最优策略是 π 1 \pi_1 π1 还是 π 2 \pi_2 π2 ?或者说,最优策略是否存在,是否唯一?是原有策略中的一个,还是对原有策略的动作进行拆分再组合?要解答这些问题,得看本文的第三章。
2.2 贝尔曼最优公式求解
贝尔曼最优公式中,有两个未知量,但式子就只有一个,求解非常具有技巧性。我们来看一个类似式子的求解:

上面的求解过程,可以归纳为一句话:max 算子可以去掉一个未知量。
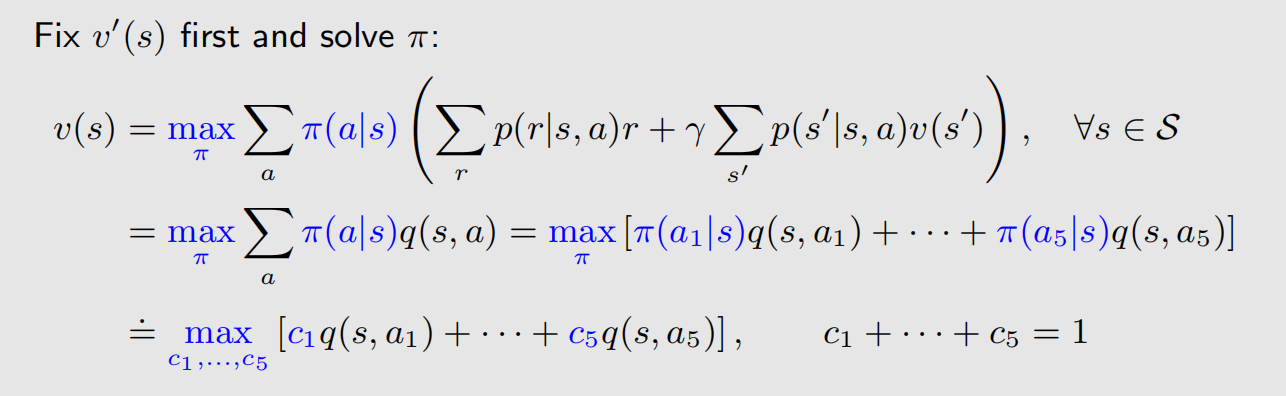
我们已经把问题转化成了一个多元线性规划问题,这个问题的解答过程如下:

简单来讲,要让目标函数最大,那么就要让最大的 q ( s , a ) q(s, a) q(s,a) 分到的权重尽可能的大。
基于前面的结论,可以得到:

至此,我们成功求解了贝尔曼最优公式。
3 矩阵形式的解
3.1 收缩映射定理(Constraction Mapping theorem)
在介绍矩阵形式的解之前,需要先介绍一下收缩映射定理。
不动点的定义:

收缩映射的定义:

截图中的 x 1 x_1 x1 和 x 2 x_2 x2 需要对定义域内的任意数值都成立。
关于收缩映射,有以下结论:

相关证明在配套的书上,前两条性质的含义好理解,第三条性质的含义表示:在一维坐标系上, x x x 从任意一个点出发,经过若干次映射迭代之后,就会趋近于不动点。
可以使用收缩映射的性质解决下面的示例:

3.2 解贝尔曼最优公式
贝尔曼最优公式(BOE),其实是收缩映射,配套的书上有证明。

可以使用收缩映射的性质求解 BOE,这种方法称为"值迭代算法(value iteration algorithm)":

3.3 贝尔曼最优公式解的最优性
通过收缩映射的性质拿到解 υ ∗ \upsilon^* υ∗ 后,假设 υ ∗ \upsilon^* υ∗ 对应的最优策略为 π ∗ \pi^* π∗,那么可以把 max 算子去掉,把贝尔曼最优公式转化成贝尔曼公式(BOE是一个特殊的贝尔曼公式,是采取最优策略时的贝尔曼公式):



4 最优策略的有趣性质
4.1 影响最优策略的因素
最优策略受 υ ∗ \upsilon^* υ∗ 影响,那么 υ ∗ \upsilon^* υ∗ 的影响因素其实就是最优策略的影响因素。下面的截图里的BOE公式,我们要根据红色的量去计算黑色的量,那么影响黑色量取值的,自然是黑色的量:

4.2 改变折扣率

上图中,没有提及的步骤,比如从白色格子到白色格子,奖励是0。
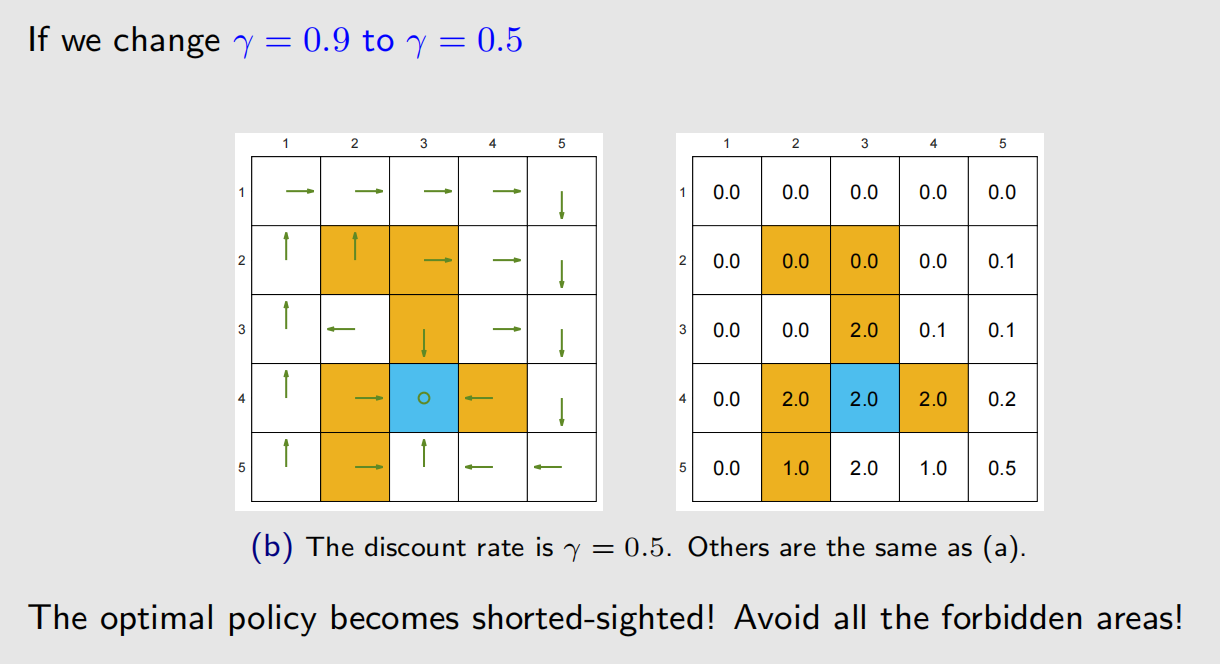
γ \gamma γ 比较大时,智能体会比较远视, γ \gamma γ 比较小时。
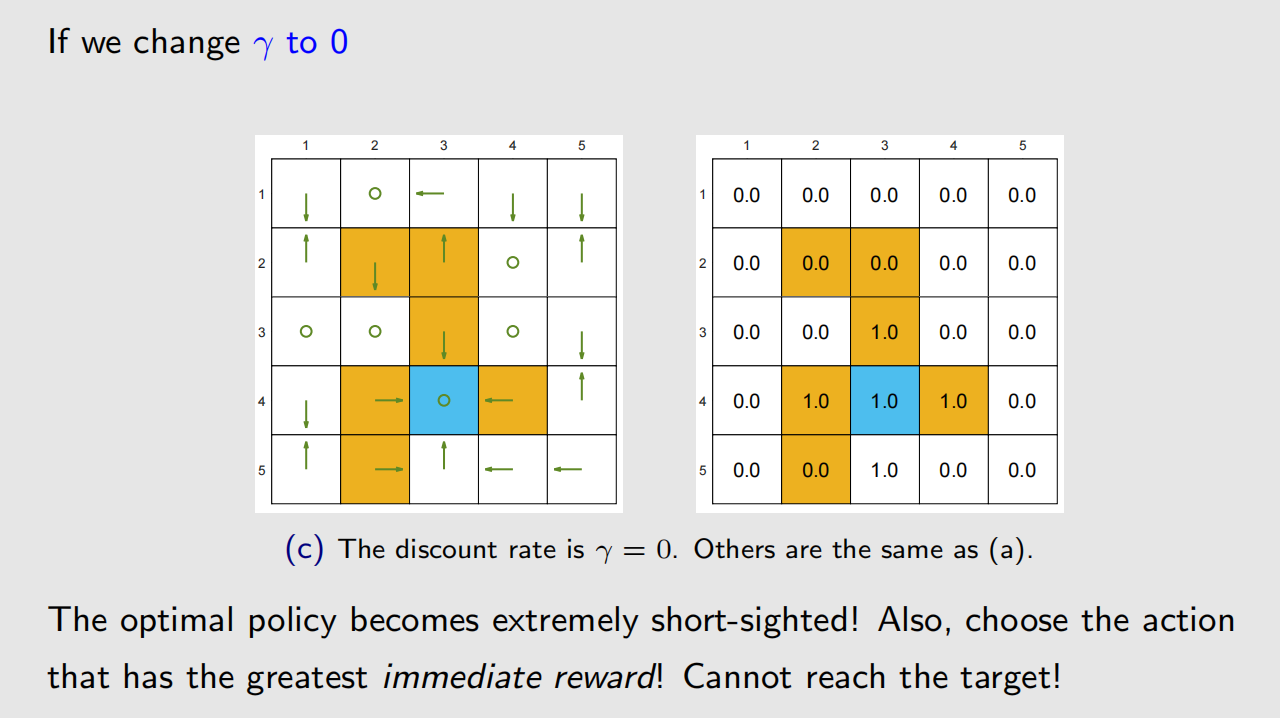
4.3 改变奖励机制
保持 γ = 0.9 \gamma=0.9 γ=0.9,修改禁区的奖励分数:

奖励分数的改动,是否影响最优策略,看的是改动前后,不同状态转移时奖励的大小顺序是否改变,如果没发生改变,那么不会影响最后得到的最优策略。比如对所有状态转移的奖励,进行统一的线性改变:

上述性质被称为最优策略的不变性。
对奖励进行线性变换,不改变最优策略,但会改变采取最优策略时的状态价值函数:

5 总结