文章Difference between AutoEncoder (AE) and Variational AutoEncoder (VAE) | Towards Data Science的解释十分清晰明了,下面将原文翻译下来,并用【】给出批注。
自编码器(AE)与变分自编码器(VAE)的区别
你如何压缩数据,甚至从随机值中生成数据?这就是自编码器和变分自编码器的定义。
简化的能力意味着去除不必要的,使必要的事物能够发声------ 汉斯·霍夫曼
Context--- Data compression
数据压缩是神经网络训练中至关重要的阶段。其理念是压缩数据,使相同信息量可以用更少的比特数表示。这也有助于解决维度诅咒的问题。高维特征空间的数据集在训练过程中更容易产生过拟合现象。因此,在数据集用于训练之前,需要先应用降维技术。
这时,自动编码器(AE)和变分自编码器(VAE)就发挥了作用。它们是端到端的网络,用于压缩输入数据。自编码器和变分自编码器都用于将数据从高维空间转换到低维空间,本质上实现压缩。
Autoencoder --- AE
自编码器用于学习给定网络配置下未标记数据的高效嵌入。自编码器由编码器和解码器两个部分组成。编码器将高维空间的数据压缩到低维空间(也称为潜在空间),而解码器则相反,即把潜在空间转换回高维空间。解码器的作用是通过强制其重构输入数据,从而确保潜空间能够保留数据空间中的大部分信息。【即,通过最小化损失函数,保证潜空间有效性】
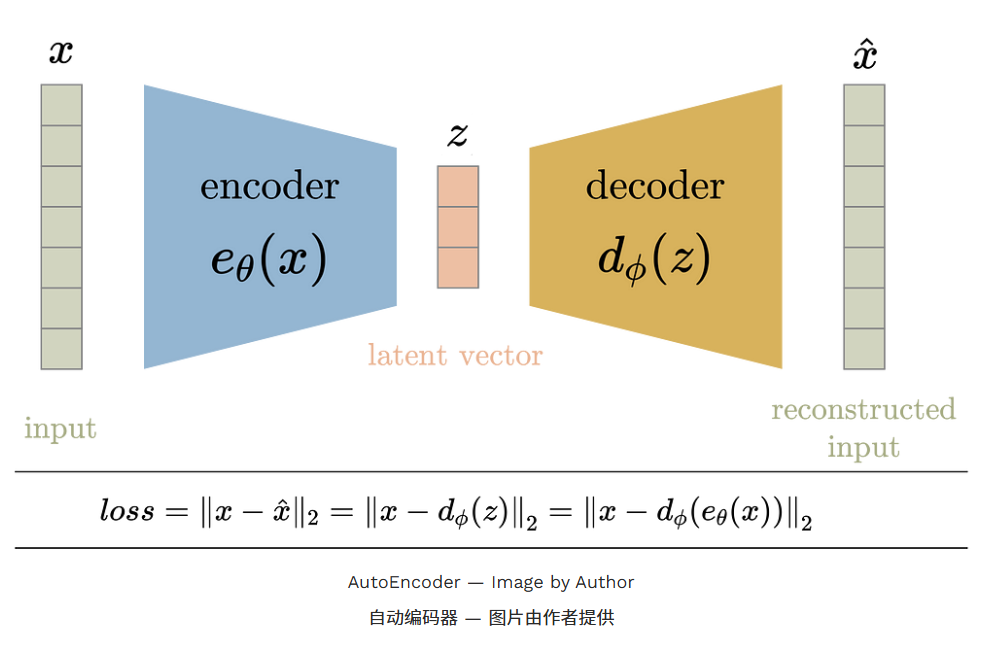
在训练过程中,输入数据 x 会被输入到编码函数 e θ ( x ) e_{\theta}(x) eθ(x)。输入通过一系列层(由变量θ参数化 )传递,降低其尺寸以获得压缩的潜在向量 z 。图层数量、层的类型和大小以及潜在空间维度都是用户控制的参数。当潜在空间的维数小于输入空间时,即可实现压缩,本质上消除了冗余属性。
解码器 d ϕ ( z ) d_{\phi}(z) dϕ(z) 通常(但不一定)由编码器中使用的层的近补层组成,但顺序相反。层的近补层是指可以用来在一定程度上撤销原层作的层,比如换位层到换层、池化到解集、完全连通到完全连通等。
整个编码器-解码器架构都集中训练于损耗函数,这鼓励输入在输出处被重建。因此,损耗函数是编码器输入与解码器输出之间的均方误差。
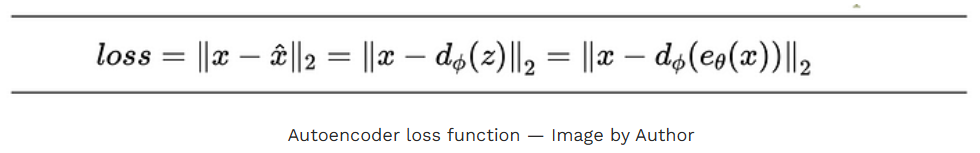
其理念是拥有一个非常低维的潜空间,以实现最大压缩,同时误差足够小。将潜空间的维数降低到某个值之外,会导致信息的显著损失。
对于潜在空间的值/分布没有任何约束。它可以是任何东西,只要能在应用解码器函数时重建输入。
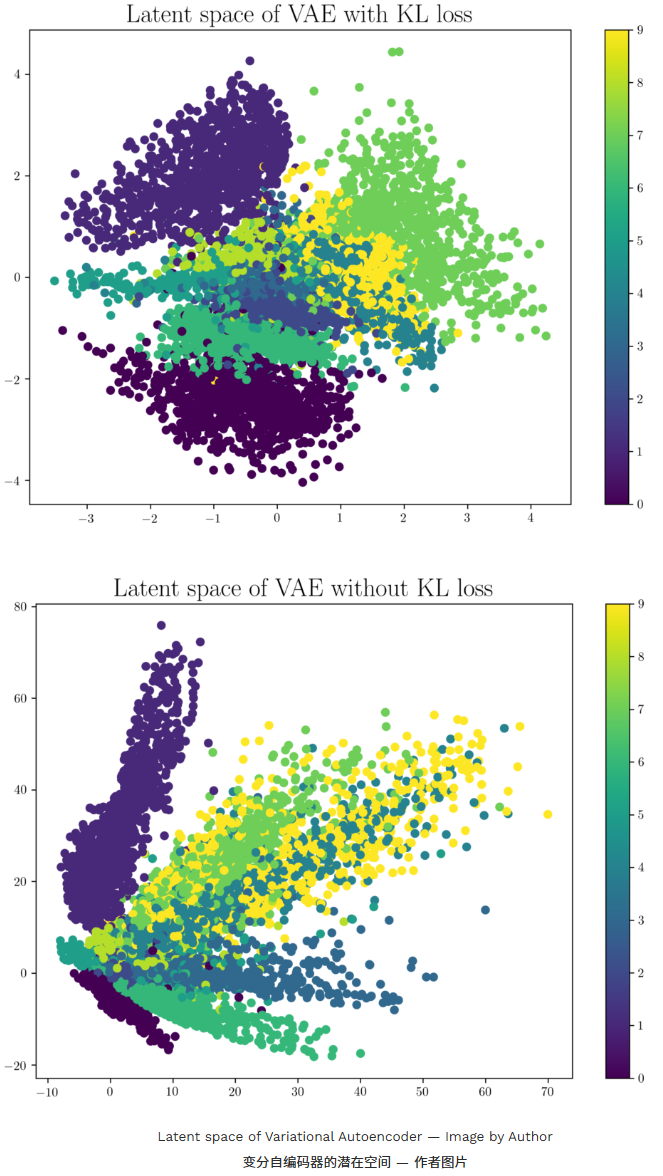
以下是通过在 MNIST 数据集上训练网络生成的潜在空间示例。
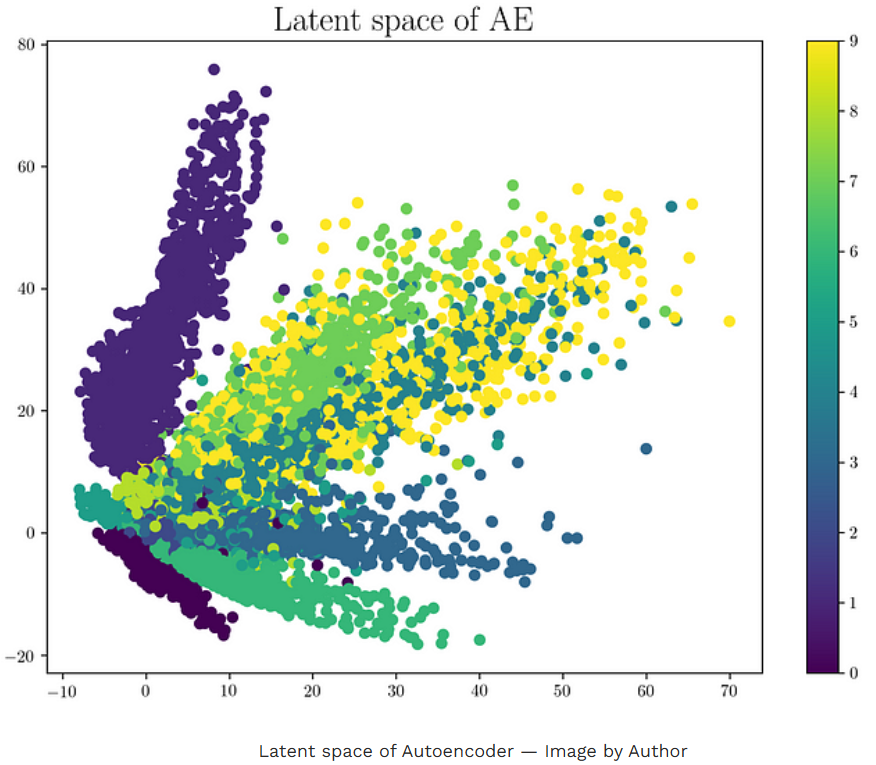
可以看出,相同的数字往往会聚集在潜在空间中。另一个重要的是,潜空间中存在不对应任何数据点的部分 。用这些数字作为编码器的输入,输出看起来和 MNIST 数据中的数字都不一样。这就是我们所说的潜在空间不正则化 的意思。这样的潜在空间只有少数区域或簇具备生成能力,这意味着采样属于簇的潜空间中任意一点,都会产生簇所属数据的变体。但整个潜在空间并不具备生成能力。不属于任何集群的区域会产生垃圾输出。一旦网络训练完成,训练数据被移除,我们就无法知道解码器从随机采样的潜在向量生成的输出是否有效。因此,AE 主要用于压缩。
对于有效输入,AE 能够将其压缩为更少的位,基本上消除冗余(编码器),但由于非正则化的潜在空间 AE,解码器无法从从潜在空间采样的向量中生成有效输入数据。
线性自编码器的潜空间与数据主分量分析时获得的特征空间非常相似。一个输入空间维数为 n 、潜在空间维数设为 m<n 的线性自编码器,结果将生成与 PCA 前 m 个特征向量相同的向量空间。如果 AE 和 PCA 类似,为什么还要用 AE?AE 的力量在于其非线性。增加非线性(如非线性激活函数和更多隐藏层)使 AE 能够在较低维度中学习输入数据的强大表示,且信息损失大幅减少。【AE能压缩数据的更本质原因】
Variational AutoEncoders --- VAE
变分自编码器解决了自编码器中非正则化的潜在空间问题,并为整个空间提供了生成能力。AE 中的编码器输出潜在矢量。VAE 的编码器不会输出潜空间中的向量,而是对每个输入输出预定义的分布参数。VAE 随后对该潜在分布施加约束,使其为正态分布。该约束确保潜空间是正则化的。
VAE 的框图如下所示。在训练过程中,输入数据 x 会被输入到编码函数 e θ ( x ) e_{\theta}(x) eθ(x)。与 AE 类似,输入通过一系列层(由变量θ参数化)传递,降低其维度以获得压缩的潜在向量 z 。然而,潜在矢量并非编码器的输出。相反,编码器输出每个潜在变量的平均值和标准差 。然后从均值和标准差中抽取潜在向量,再送入解码器重建输入。VAE 中的解码器工作原理类似于 AE 中的解码器。
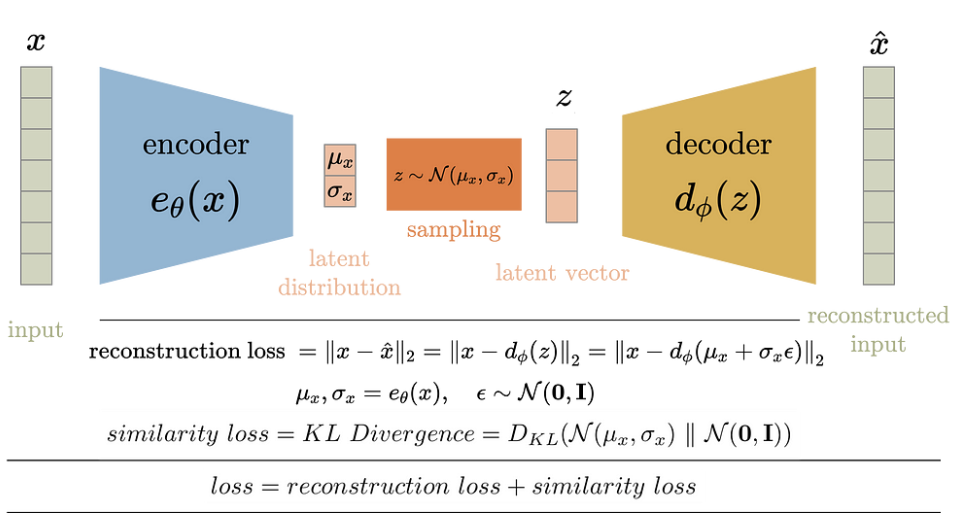
损耗函数由 VAE 目标定义。VAE 有两个目标:
- Reconstruct the input 重建输入
- Latent space should be normally distributed 潜在空间应为标准正态分布
因此,VAE 的训练损失被定义为 重建损失 和 相似性损失 的总和。重建误差,就像 AE 一样,是输入和重建输出的均方损失。相似性损失是潜空间分布与标准高斯分布(均值和单位方差为零)之间的 KL 散度。损失函数则是这两个损失的总和。
如前所述,潜在矢量在输入解码器前从编码器生成的分布中取样。这种随机采样使编码器难以进行反向传播,因为我们无法追溯因随机采样产生的错误 。因此,我们使用重新参数化 技巧来模拟采样过程,使误差能够在网络中传播。潜在矢量 z 表示为编码器输出的函数。【reparameterization 技巧就是将正态分布采样转化为标准高斯采样+线性运算。】

训练试图在两种损失之间找到平衡,最终得到一个潜在空间分布,看起来像单位范数,并以聚类方式组合相似的输入数据点。单位范数条件确保潜空间均匀分布,且簇间没有显著间隙。事实上,相似数据输入的集群在某些区域通常会重叠。以下是在同一 MNIST 数据集上训练网络生成的潜在空间示例,该数据集用于可视化 AE 的潜在空间。注意簇间没有空隙,空间类似于单位范数分布。
【"找到平衡"意味着模型既要保证输入被良好重建,又要保持潜在空间分布接近标准正态(或者单位范数球面),这两者有时会冲突。"单位范数"通常指潜在向量 z 的长度接近 1,即 ∣ ∣ z ∣ ∣ ≈ 1 ∣∣z∣∣\approx 1 ∣∣z∣∣≈1。相似的数据(比如 MNIST 中的数字"0")在潜在空间里会靠得很近,形成簇(cluster),即聚类方式。】
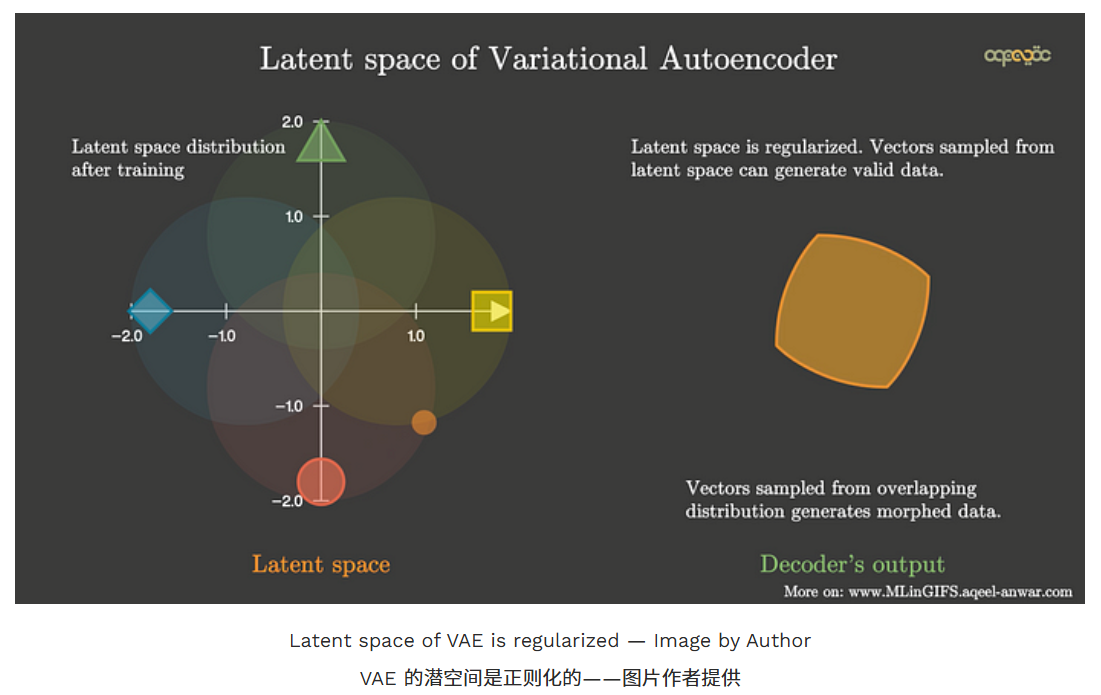
需要注意的是,当潜在向量从有重叠聚簇的区域采样时,我们得到的是变形数据。当我们采样潜在空间从一个簇移动到另一个簇时,解码器的输出之间会有一个平滑的过渡。
Summary
本文介绍了主要用于数据压缩和数据生成的自编码器(AE)和变分自编码器(VAE)的理解。VAE 解决了 AE 中非正则化潜空间的问题,使其能够从潜空间中随机采样的向量生成数据。AE 和 VAE 的关键总结点是:
Autoencoder
· Used to generate a compressed transformation of input in a latent space
·用于生成潜在空间输入的压缩变换
· The latent variable is not regularized
·潜变量不被正则化
· Picking a random latent variable will generate garbage output
·选择随机潜在变量会产生垃圾输出
· The latent variable has a discontinuity
·潜变量存在不连续点
· Latent variable is deterministic values
·潜在变量是确定性值
· The latent space lacks the generative capability
·潜伏空间缺乏生成能力
Variational Autoencoder
· Enforces conditions on the latent variable to be the unit norm
·强制对潜变量的条件为单位范数
· The latent variable in the compressed form is mean and variance
·压缩形式中的潜变量是均值和方差
· The latent variable is smooth and continuous
·潜变量是平滑且连续的
· A random value of latent variable generates meaningful output at the decoder
·潜在变量的随机值在解码器处产生有意义的输出
· The input of the decoder is stochastic and is sampled from a gaussian with mean and variance of the output of the encoder.
·译码器的输入是随机的,采样自一个高斯算图,输出的均值和方差。
· Regularized latent space
·正则化潜空间
· The latent space has generative capabilities.
·潜伏空间具备生成能力。
原作者信息:If this article was helpful to you or you want to learn more about Machine Learning and Data Science, follow Aqeel Anwar, or connect with me on LinkedIn or Twitter.