目录
1.神经元的MP模型
1943年,沃伦·麦卡洛克(Warren McCulloch)和沃尔特·皮茨(Walter Pitts)提出了对神经元高度简化的抽象模型--MP模型。先看两者的结构图:
神经元生理结构图:
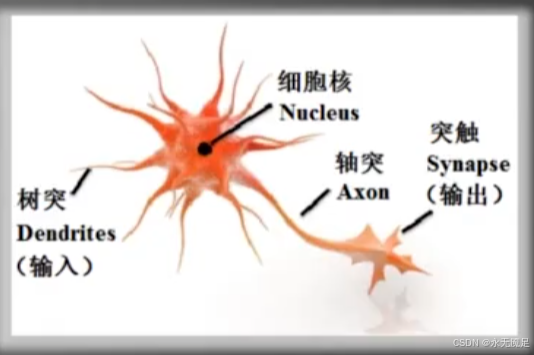
神经元数学模型图:
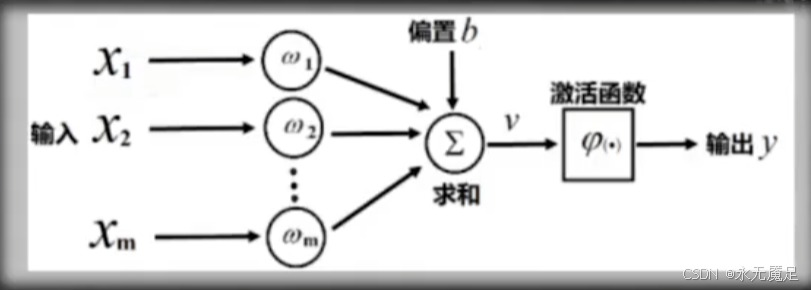
MP模型将外部刺激看作输入~
,将树突对输入的加工处理过程看作对输入的加权,将细胞核对输入的处理看作加权后的输入以及偏置b的求和过程。最后的输出就是通过激活函数进行非线性变换得到的。
根据以上过程就可以得出该模型中输入和输出的对应关系为: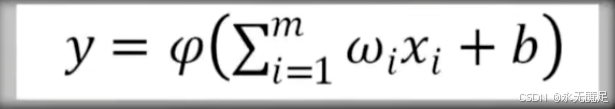
通过对和
(i=1~m)进行向量形式的转换:即
,
将上式转换为:
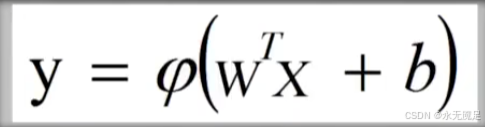
2.感知器
1957年Frank Rosenblatt从纯数学的角度重新考察神经元的MP模型,指出通过机器学习的方法能够能从一些输入输出对自动获取其中的权重W和偏置b,由此提出了感知器算法,具体过程如下:

首先进行感知器的初始化(随机选取权重和偏置),再选取一个训练样本(X为训练数据,y为对应的标签),如果没有达到平衡,那么更新权重和偏置后再选取一个训练样本判断,直到所有输入输出对都达到了平衡,则退出循环。
以上说的平衡指的就是,y=-1的训练样本,我们期望,而y=+1的训练样本,我们期望
。
3.线性可分与线性不可分
3.1定义
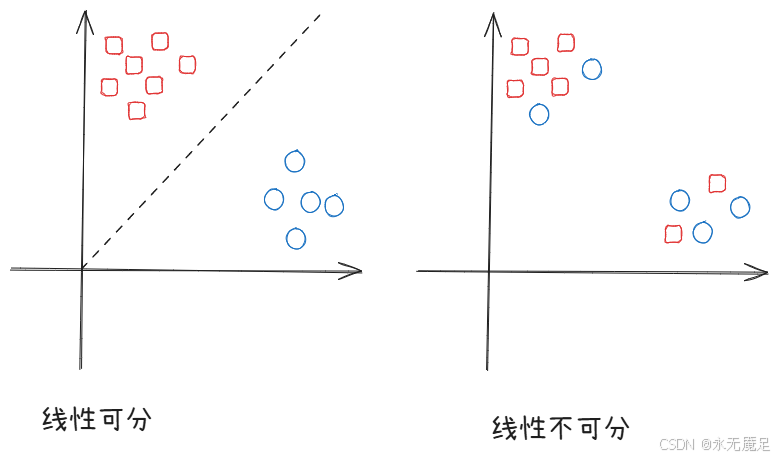
假设在二维空间中,使用一条直线可以将样本完美分类,即为线性可分,否则为线性不可分。
上升到三维空间中,该直线升为面;在三维之上的空间,该直线升为超平面。
如图便是两种示例:
3.2数学定义
重新回到二维空间讨论该问题,如图:
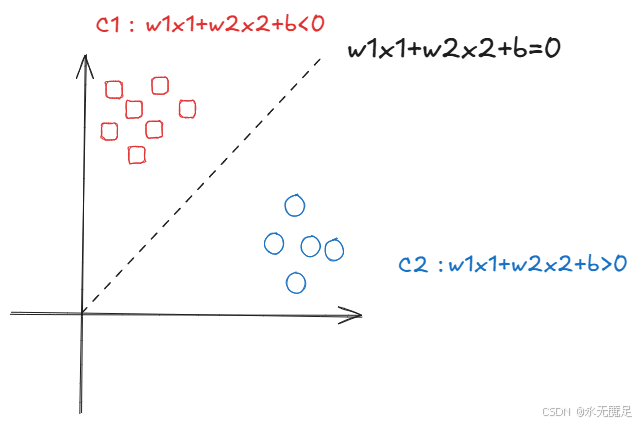
假设现在有圈和方两类样本,从图中可以看到这条直线将它们完美分开,假设方所在的区域为C1,即
;圆所在的区域为C2,即
。
我们怎么判断样本被分类正确? 即通过标签和被划分区域的一致性,假设标签y=+1的样本应该被划分到C1,标签y=-1的样本应该被划分到C2,那么样本被正确分类的情况如下:
以上我们讨论的是一个样本的情况。现在,假设有N个训练样本,记为,i=1~N。每个样本都有一个标签
。因为这些样本是处在二维空间中,所以它们每一个都是由
和
决定的。
可以把样本看作在空间中的点(),在二维空间中就是通过横轴(
)和竖轴(
)结合起来确定一个点。
**形式(1):**由此,对线性可分严格的数学定义如下:

**形式(2):**用和第1节中提到的向量转换方法,可将任务描述转换为:

形式(3): 如果引入增广向量形式:对于某个样本,定义其增广向量如下:

这样就可以将原本任务简述为:

注意,。
4.感知器收敛定理
在第2节中有一个问题,有没有可能在使得一个样本达到平衡状态之后同时又使得另一个原本已经达到平衡状态的样本转为不平衡的状态?
感知器收敛定理指明:当数据集线性可分的时候,一定会在有限步内找到合适的w和b使得所有样本达到平衡状态,如图:

其上面的条件,实际就是表述数据集线性可分。
需要注意的是,根据线性可分定义有:如果有一个超平面可以分开两类,那么一定有无数个超平面可以分开两类。由此结论可以得出感知器最后找到的W不一定就是,有可能只是无数超平面中的其中两个。