I n f o r m e r Informer Informer
摘要:
长序列时间序列的预测
i n f o r m e r informer informer优点:
- P r o b s p a r e Probspare Probspare自关注机制,在时间复杂度和内存使用方面达到 O ( N l o g N ) O(NlogN) O(NlogN),在序列依赖对齐方面性能较好。
- 自注意蒸馏通过将级联层输入减半来突出主导注意力,并有效地处理极长的输入序列。
- 以一次向前操作的方式预测长序列时间序列,提高了长序列预测的推理速度。
1.简介:
T r a n s f o r m e r Transformer Transformer求解 L S T F LSTF LSTF缺点:
- 自注意力的二次计算。标准的点积 ( d o t − p r o d u c t ) (dot-product) (dot−product)操作,会导致每一层的时间复杂度和内存使用都达到 O ( N 2 ) O(N^2) O(N2)的级别,其中 L L L是输入序列的长度。
- 长输入的堆叠层的内存瓶颈。 J J J编码器/解码器层的堆叠使得总内存使用量为 O ( J ⋅ L 2 ) O(J·L^2) O(J⋅L2),这限制了模型在接收长序列输入时的可扩展性。
- 预测长期产出的速度下降。原始 T r a n s f o r m e r Transformer Transformer的动态解码使得逐步推理与基于 R N N RNN RNN的模型一样慢,每个步骤都必须等待前一个步骤完成才能进行。
本文主要内容:
- 提出了 I n f o r m e r Informer Informer来成功地增强 L S T F LSTF LSTF问题的预测能力,这验证了类似 T r a n s f o r m e r Transformer Transformer模型的潜在价值,以捕捉长序列时间序列输出和输入之间的单个长期依赖关系。
- 提出了 P r o b S p a r s e ProbSparse ProbSparse自注意机制来有效地取代规范的自注意机制,实现了 O ( N l o g N ) O(NlogN) O(NlogN)的时间复杂度和 O ( N l o g N ) O(NlogN) O(NlogN)的内存使用。
- 提出了自注意力蒸馏操作特权支配 j − j- j−堆叠层的注意力分数,并大幅降低总空间复杂度为 O ( ( 2 − ϵ ) N l o g N ) O((2−\epsilon)NlogN) O((2−ϵ)NlogN)。
- 提出生成式解码器 ( G e n e r a t i v e S t y l e D e c o d e r ) (Generative Style Decoder) (GenerativeStyleDecoder),只需要向前一步就可以获得长序列输出,同时避免累积错误传播
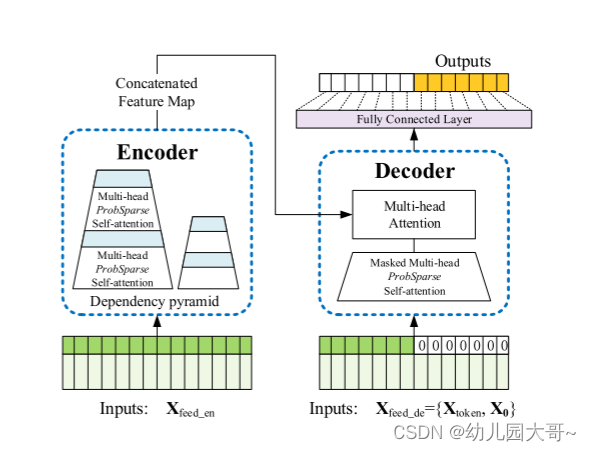
I n f o r m e r Informer Informer模型的整体图。左边的部分是 E n c o d e r Encoder Encoder,它接收大量的长序列输入(绿色系列)。我们已经用提出的 P r o b S p a r s e ProbSparse ProbSparse自注意取代了规范的自注意。蓝色梯形是提取支配性注意的自注意蒸馏操作,急剧减小网络规模。层堆叠副本提高了鲁棒性。对于右侧部分,解码器接收长序列输入,将目标元素填充为零,测量特征图的加权注意力组成,并以生成式的方式立即预测输出元素(橙色系列)。
2.预备
定义:在具有固定大小窗口的滚动预测设置下,在 t t t时刻的输入为 X t = { x t 1 , ... , x t L x ∣ x t i ∈ R d x } X_t = \{ x_t^1, \ldots, x_t^{L_x} \,|\, x_t^i \in \mathbb{R}^{d_x} \} Xt={xt1,...,xtLx∣xti∈Rdx},输出为 Y t = { y t 1 , ... , y t L y ∣ y t i ∈ R d y } Y_t = \{ y_t^1, \ldots, y_t^{L_y} \,|\, y_t^i \in \mathbb{R}^{d_y} \} Yt={yt1,...,ytLy∣yti∈Rdy}
编码器-解码器架构 ( E n c o d e r − d e c o d e r a r c h i t e c t u r e ) (Encoder-decoder\ architecture) (Encoder−decoder architecture)被设计用于将输入表示 X t X_t Xt "编码"为隐藏状态表示 H t H_t Ht,并从 H t = h t 1 , . . . , h t L h H_t = {h_t^1, ..., h_t^{L_h}} Ht=ht1,...,htLh 中"解码"出输出表示 Y t Y_t Yt。推理过程涉及一个名为"动态解码" ( d y n a m i c d e c o d i n g ) (dynamic\ decoding) (dynamic decoding)的逐步过程,其中解码器根据前一个状态 h t k h_t^k htk和第 k k k 步的其他必要输出,计算新的隐藏状态 h t k + 1 h_t^{k+1} htk+1,然后预测第 ( k + 1 ) (k+1) (k+1) 个序列 y t k + 1 y_t^{k+1} ytk+1。
在这个架构中,编码器负责处理输入数据(例如,一个句子、一段文本、一个图像等),并将其转换为一个或多个隐藏状态向量。这些隐藏状态向量捕获了输入数据的重要信息,这些信息随后被解码器用来生成输出序列。
解码器则负责利用这些隐藏状态向量来生成输出数据。在生成输出时,解码器通常会采用一种序列到序列 ( s e q u e n c e − t o − s e q u e n c e ) (sequence-to-sequence) (sequence−to−sequence)的方法,即一个步骤接着一个步骤地生成输出序列。在每个步骤中,解码器都会考虑前一个步骤的输出和隐藏状态,来预测下一个输出。
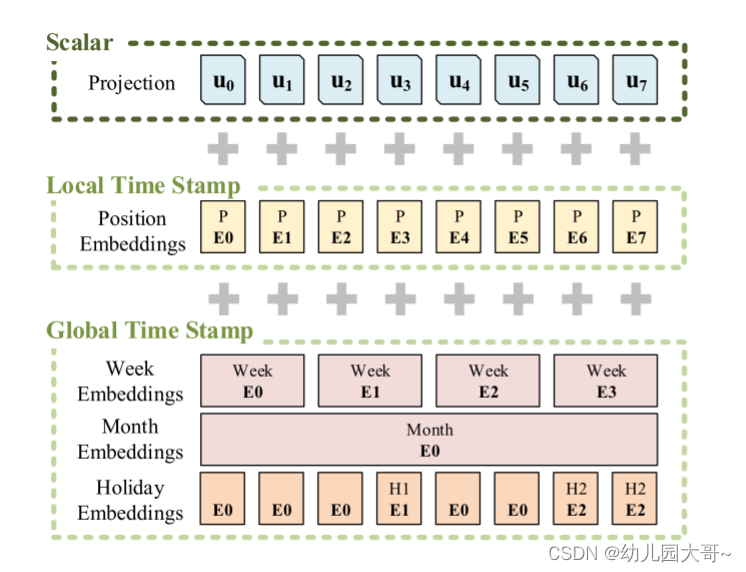
Informer的输入表示,包括标量投影,本地时间戳和全局时间戳嵌入三个部分.jpg
假设我们有 t t t个序列输入 X t X_t Xt和 p p p种类型的全局时间戳,输入表示后的特征维度为 d m o d e l d_{model} dmodel。我们首先通过使用固定位置嵌入来保持低阶上下文,即 P E ( p o s , 2 j ) = sin ( p o s ( 2 L x ) 2 j / d model ) PE(pos, 2j) = \sin\left(\frac{pos}{{(2L_x)}^{2j/d_{\text{model}}}}\right) PE(pos,2j)=sin((2Lx)2j/dmodelpos),
P E ( p o s , 2 j + 1 ) = cos ( p o s ( 2 L x ) 2 j / d model ) PE(pos, 2j+1) = \cos\left(\frac{pos}{{(2L_x)}^{2j/d_{\text{model}}}}\right) PE(pos,2j+1)=cos((2Lx)2j/dmodelpos),,其中 j ∈ { 1 , ... , d model 2 } j \in \left\{1, \ldots, \frac{d_{\text{model}}}{2}\right\} j∈{1,...,2dmodel}.。每个全局时间戳由一个可学习的戳嵌入 S E ( p o s ) SE_{(pos)} SE(pos)使用,词汇表大小有限(最多 60 60 60个,即以分钟为最细粒度)。也就是说,自注意力的相似度计算可以访问全局上下文,并且在长输入上的计算开销是可以承受的。为了对齐维度,我们使用一维卷积滤波器(核宽度= 3 3 3,步长= 1 1 1)将标量上下文 x i t x_{i}^{t} xit投影 d m o d e l d_{model} dmodel-维向量 u i t u_{i}^{t} uit。因此,我们有了如下的f反馈向量: X feed[i] t = α u i t + PE ( L x × ( t − 1 ) + i ) + ∑ p [ SE ( L x × ( t − 1 ) + i ) ] p X_{\text{feed[i]}}^t = \alpha u_i^t + \text{PE}(L_x \times (t-1) + i) + \sum_{p} \left[ \text{SE}{(L_x \times (t-1) + i)} \right]{\text{p}} Xfeed[i]t=αuit+PE(Lx×(t−1)+i)+∑p[SE(Lx×(t−1)+i)]p,其中 i ∈ { 1 , ... , L x } i \in \{1, \dots, L_x\} i∈{1,...,Lx},并且 α α α是一个用于平衡标量投影与局部/全局嵌入之间的幅度的因子。如果序列输入已经被标准化了,我们推荐 α = 1 α=1 α=1。这里的PE代表位置嵌入 ( p o s i t i o n e m b e d d i n g ) (position\ embedding) (position embedding),用于捕捉序列中每个位置的信息;而 S E SE SE是学习的时间戳嵌入 , α α α是一个超参数,用于平衡不同的嵌入或投影对最终输入向量的贡献。
3.方法论
高效自我注意机制
自注意力机制接收一个元组输入 ( q u e r y , k e y , v a l u e ) (query, key, value) (query,key,value),并通过缩放点积运算 ( s c a l e d d o t − p r o d u c t ) (scaled dot-product) (scaleddot−product)进行运算,表示为 A ( Q , K , V ) = Softmax ( Q K ⊤ d ) V , 其中 Q ∈ R L Q × d , K ∈ R L K × d , V ∈ R L V × d A(Q, K, V) = \text{Softmax}\left(\frac{QK^{\top}}{\sqrt{d}}\right)V, \text{其中 } Q \in \mathbb{R}^{L_Q \times d}, K \in \mathbb{R}^{L_K \times d}, V \in \mathbb{R}^{L_V \times d} A(Q,K,V)=Softmax(d QK⊤)V,其中 Q∈RLQ×d,K∈RLK×d,V∈RLV×d,其中 d d d 是输入维度。为了进一步讨论自注意力机制,令 q i q_i qi, k i k_i ki, v i v_i vi 分别表示 Q Q Q, K K K, V V V 中的第 i i i 行。根据 T s a i e t a l . ( 2019 ) Tsai \ et\ al. (2019) Tsai et al.(2019) 的公式,第 i i i 个查询的注意力被定义为概率形式的核平滑器 ( k e r n e l s m o o t h e r ) (kernel\ smoother) (kernel smoother): 则:
A ( q i , K , V ) = ∑ j k ( q i , k j ) ∑ l k ( q i , k l ) v j = E p ( k j ∣ q i ) [ v j ] 方程一 A(q_i, K, V) = \sum_j \frac{k(q_i, k_j)}{\sum_l k(q_i, k_l)} v_j=\mathbb{E}_{p(k_j|q_i)}[v_j] \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 方程一 A(qi,K,V)=j∑∑lk(qi,kl)k(qi,kj)vj=Ep(kj∣qi)[vj] 方程一
其中, p ( k j ∣ q i ) = k ( q i , k j ) ∑ l k ( q i , k l ) p(k_j|q_i) = \frac{k(q_i, k_j)}{\sum_l k(q_i, k_l)} p(kj∣qi)=∑lk(qi,kl)k(qi,kj) , k ( q i , k j ) k(q_i, k_j) k(qi,kj) 是一个核函数。这里我们使用不对称的指数核函数 exp ( q i ⋅ k j d ) \exp\left(\frac{q_i \cdot k_j}{\sqrt{d}}\right) exp(d qi⋅kj)。自注意力机制通过计算概率 (p(k_j\|q_i)) 来结合值并获取输出。这需要二次时间复杂度的点积计算和 ( O ( L Q L K ) ) (O(L_Q L_K)) (O(LQLK)) 的内存使用,这是提高预测能力的主要缺点。
从方程 ( 1 ) (1) (1)中,第 ( i ) (i) (i)个查询对所有键的注意力被定义为一个概率 ( p ( k j ∣ q i ) ) (p(k_j|q_i)) (p(kj∣qi)),而输出是其与值 ( v ) (v) (v)的组合。主要的点积对会鼓励对应的查询注意力概率分布远离均匀分布。如果 ( p ( k j ∣ q i ) ) (p(k_j|q_i)) (p(kj∣qi))接近均匀分布 ( q ( k j ∣ q i ) = 1 L K ) (q(k_j|q_i) = \frac{1}{L_K}) (q(kj∣qi)=LK1),那么自注意力就变成了值 ( V ) (V) (V)的简单和,并且对输入是冗余的。自然地,分布 ( p ) (p) (p) 和 ( q ) (q) (q)之间的"相似性"可以用来区分"重要"的查询。我们通过 K u l l b a c k − L e i b l e r Kullback-Leibler Kullback−Leibler散度( K L KL KL散度)来测量"相似性", K L KL KL散度定义为:
K L ( q ∣ ∣ p ) = ln ( ∑ l = 1 L K e q i ⋅ k l T d ) − ln ( L K ) − ∑ j = 1 L K 1 L K ⋅ q i ⋅ k l T d \begin{equation*} KL(q||p) = \ln\left( \sum_{l=1}^{L_K} e^{\frac{q_i \cdot k_l^T}{\sqrt{d}}} \right) - \ln(L_K) - \sum_{j=1}^{L_K} \frac{1}{L_K} \cdot {\frac{q_i \cdot k_l^T}{\sqrt{d}}} \end{equation*} KL(q∣∣p)=ln(l=1∑LKed qi⋅klT)−ln(LK)−j=1∑LKLK1⋅d qi⋅klT
我们定义第 ( i ) (i) (i) 个查询的稀疏度测量为:
M ( q i , K ) = ln ( ∑ j = 1 L K e q i ⋅ k j T d ) − 1 L K ∑ j = 1 L K q i ⋅ k j T d 方程二 M(q_i, K) = \ln\left( \sum_{j=1}^{L_K} e^{\frac{q_i \cdot k_j^T}{\sqrt{d}}} \right) - \frac{1}{L_K} \sum_{j=1}^{L_K} \frac{q_i \cdot k_j^T}{\sqrt{d}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 方程二 M(qi,K)=ln(j=1∑LKed qi⋅kjT)−LK1j=1∑LKd qi⋅kjT 方程二
第一项是所有键上 ( q i ) (q_i) (qi) 的 L o g − S u m − E x p ( L S E ) Log-Sum-Exp(LSE) Log−Sum−Exp(LSE),第二项是这些键的算术平均值。如果第 ( i ) (i) (i)个查询获得了较大的 ( M ( q i , K ) ) (M(q_i, K)) (M(qi,K))值,那么它的注意力概率 ( p ) (p) (p) 就更加"多样化",并且有很大可能性包含长尾自注意力分布中头部字段的主要点积对。这里,"多样化"意味着注意力不仅仅集中在少数几个键上,而是相对均匀地分布在多个键上。同时,由于 ( M ( q i , K ) ) (M(q_i, K)) (M(qi,K)) 值较大,该查询的注意力分布更有可能包含那些具有较大点积值的键-查询对,这些对在长尾分布中占据主导地位。
基于所提出的度量标准,我们通过允许每个键仅关注于占主导地位的查询u,从而实现了 P r o b S p a r s e ProbSparse ProbSparse自注意力机制。
A ( Q , K , V ) = Softmax ( Q ‾ K T d ) V 方程三 A(Q, K, V) = \text{Softmax}\left(\frac{\overline QK^T}{\sqrt{d}}\right)V\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 方程三 A(Q,K,V)=Softmax(d QKT)V 方程三
其中, ( Q ‾ ) (\overline Q) (Q)是一个与 ( q ) (q) (q) 相同大小的稀疏矩阵,它仅包含根据稀疏性度量 ( M ( q , K ) ) (M(q,K)) (M(q,K)) 选择的前 ( u ) (u) (u) 个查询。通过一个常数采样因子 ( c ) (c) (c) 来控制,我们设定 ( u = c ⋅ ln L Q ) (u = c \cdot \ln L_Q) (u=c⋅lnLQ),这使得 P r o b S p a r s e ProbSparse ProbSparse 自注意力机制在每次查询-键查找时只需要计算 ( O ( ln L Q ) ) (O(\ln L_Q)) (O(lnLQ)) 个点积,并且层的内存使用保持在 ( O ( L K ln L Q ) ) (O(L_K \ln L_Q)) (O(LKlnLQ))。
简单来说, P r o b S p a r s e ProbSparse ProbSparse 自注意力机制通过稀疏化手段,仅对稀疏矩阵 ( Q ) (Q) (Q)中的前 ( u ) (u) (u)个查询(根据某种稀疏性度量)进行计算,从而降低了计算复杂度和内存使用。这里的 ( u ) (u) (u) 是基于查询数量 ( L Q ) (L_Q) (LQ)的对数和一个常数采样因子 ( c ) (c) (c) 来确定的。
然而,为了计算度量 ( M ( q i , K ) ) (M(q_i, K)) (M(qi,K))而遍历所有查询需要计算每对点积,即时间复杂度为平方级别的 ( O ( L Q L K ) ) (O(L_Q L_K)) (O(LQLK)),并且 L S E ( L o g − S u m − E x p ) LSE(Log-Sum-Exp) LSE(Log−Sum−Exp)操作存在潜在的数值稳定性问题。鉴于这一点,我们提出了一个查询稀疏性度量的近似方法。
引理一 :对于每个查询 q i ∈ R d q_i \in \mathbb{R}^d qi∈Rd 和键集中的 k j ∈ R d k_j \in \mathbb{R}^d kj∈Rd 在集合 K K K 中,我们有边界 ln L K ≤ M ( q i , K ) ≤ max j { q i ⋅ k j T d } − 1 L K ⋅ ∑ j = 1 L K { q i ⋅ k j T d } + ln L K \ln L_K \leq M(q_i, K) \leq \max_j \left\{ \frac{ \, q_i \cdot k_j^T}{\sqrt{d}} \right\} - \frac 1{L_K}\cdot \sum_{j=1}^{L_K} \left\{ \frac{ \, q_i \cdot k_j^T}{\sqrt{d}} \right\}+ \ln L_K lnLK≤M(qi,K)≤jmax{d qi⋅kjT}−LK1⋅j=1∑LK{d qi⋅kjT}+lnLK 。当 q i ∈ K q_i \in K qi∈K 时,该不等式也成立。
根据引理一,我们提出了最大均值测量为:
M ‾ ( q i , K ) = max j { q i ⋅ k j T d } − 1 L K ∑ j = 1 L K q i ⋅ k j T d 方程四 \overline M(q_i, K) = \max_j \left\{ \frac{q_i \cdot k_j^T}{\sqrt{d}} \right\} - \frac{1}{L_K} \sum_{j=1}^{L_K}\frac{q_i \cdot k_j^T}{\sqrt{d}} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 方程四 M(qi,K)=jmax{d qi⋅kjT}−LK1j=1∑LKd qi⋅kjT 方程四
命题一 :假设 k j ∼ N ( μ , Σ ) k_j \sim N(\mu, \Sigma) kj∼N(μ,Σ),我们让 q k i q{k_i} qki 表示集合 { ( q i k j T ) / d ∣ j = 1 , ... , L K } \left\{ \left( q_i{k_j^T} \right) / \sqrt{d} \,|\, j = 1, \ldots, L_K \right\} {(qikjT)/d ∣j=1,...,LK},那么对于 ∀ M m = max i M ( q i , K ) \forall M_m = \max_i M(q_i, K) ∀Mm=maxiM(qi,K),存在 κ > 0 \kappa > 0 κ>0 使得:在区间 ∀ q 1 , q 2 ∈ { q ∣ M ( q , K ) ∈ [ M m , M m − κ ) } \forall q_1, q_2 \in \{ q \,|\, M(q, K) \in [M_m, M_m - \kappa) \} ∀q1,q2∈{q∣M(q,K)∈[Mm,Mm−κ)} 内,如果 M ‾ ( q 1 , K ) > M ‾ ( q 2 , K ) \overline M(q_1, K) > \overline M(q_2, K) M(q1,K)>M(q2,K) 并且 Var ( q k 1 ) > Var ( q k 2 ) \text{Var}(q{k_1}) > \text{Var}(q{k_2}) Var(qk1)>Var(qk2),那么 M ( q 1 , K ) > M ( q 2 , K ) M(q_1, K) > M(q_2, K) M(q1,K)>M(q2,K) 的概率很高。为了简化,证明中给出了概率的估计。
边界放宽下的前 ( u ) (u) (u) 个的顺序在命题 1 1 1(请参阅附录 D . 2 D.2 D.2中的证明)中得以保持。在长尾分布下,我们仅需要随机抽取 ( U = L Q ln L K ) (U = L_Q \ln L_K) (U=LQlnLK)个点积对来计算 ( M ‾ ( q i , K ) ) (\overline M(q_i, K)) (M(qi,K)),即将其余的点积对填充为零。我们从中选择稀疏的前 ( u ) (u) (u)个作为 ( Q ) (Q) (Q)。在 ( M ( q i , K ) ) (M(q_i, K)) (M(qi,K)) 中的最大值操作对零值不太敏感,并且数值上是稳定的。在实践中,查询和键的输入长度通常是相等的,即 ( L Q = L K = L ) (L_Q = L_K = L) (LQ=LK=L),这样 P r o b S p a r s e ProbSparse ProbSparse自注意力的总时间复杂度和空间复杂度都是 ( O ( L ln L ) ) (O(L \ln L)) (O(LlnL))。
E n c o d e r : Encoder: Encoder:允许在内存使用限制下处理更长的顺序输入
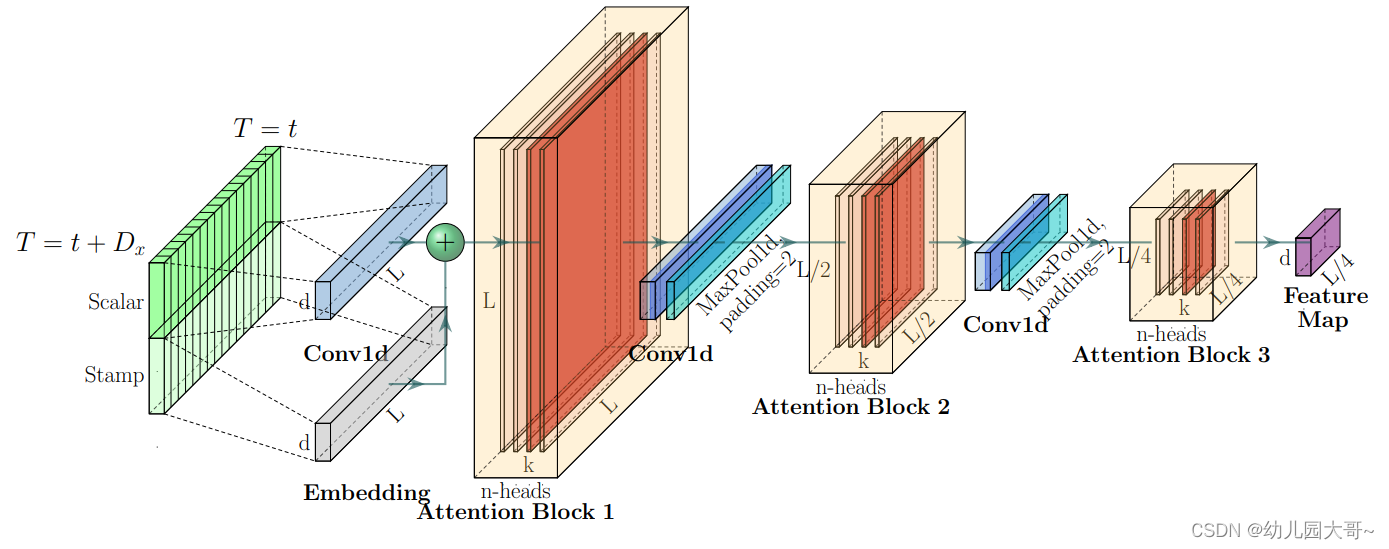
Informer编码器的架构。 (1)每个水平堆叠代表图2中的编码器副本中的一个独立副本; (2)上面的堆叠是主要堆叠,它接收整个输入序列,而第二个堆叠则接收输入的一半切片; (3)红色层是自注意力机制的点积矩阵,通过在每一层应用自注意力蒸馏技术,这些矩阵的数量逐渐减少; (4)将两个堆叠的特征图合并作为编码器的输出。
该编码器被设计用于提取长序列输入中的稳健长程依赖关系。在输入表示之后,第 t t t个序列输入 X t X_t Xt被重塑为一个大小为 L x × d model L_x \times d_{\text{model}} Lx×dmodel的矩阵 X t feed en ∈ R L x × d model X_t^{\text{feed en}} \in \mathbb{R}^{L_x \times d_{\text{model}}} Xtfeed en∈RLx×dmodel。
自注意力蒸馏 ( S e l f − a t t e n t i o n D i s t i l l i n g ) (Self-attention\ Distilling) (Self−attention Distilling)作为 P r o b S p a r s e ProbSparse ProbSparse自注意力机制的自然结果,编码器的特征图包含了冗余的值 V V V组合。我们利用蒸馏操作来突出具有主导特征的优势组合,并在下一层生成一个集中的自注意力特征图。这极大地缩减了输入的时间维度,如图中注意力模块的 n n n个头权重矩阵(重叠的红色方块)所示。受到空洞卷积 ( Y u , K o l t u n , a n d F u n k h o u s e r 2017 ; G u p t a a n d R u s h 2017 ) (Yu, Koltun, and \ Funkhouser \ 2017; Gupta \ and \ Rush \ 2017) (Yu,Koltun,and Funkhouser 2017;Gupta and Rush 2017)的启发,我们的"蒸馏"过程从第 j j j层向前传递到第 ( j + 1 ) (j+1) (j+1)层,作为
X t j + 1 = MaxPool ( ELU ( Conv1d [ X t j ] A B ) ) 方程五 X_{t}^{j+1} = \text{MaxPool}\left( \text{ELU}\left( \text{Conv1d}\ \left[ X_{t}^{j} \right]_{AB} \right) \right)\ \ \ \ \ \ \ \ \ \ \ \ \ 方程五 Xtj+1=MaxPool(ELU(Conv1d [Xtj]AB)) 方程五
其中,该表达式 [ ⋅ ] A B [·]_{AB} [⋅]AB包含多头ProbSparse自注意力机制以及注意力块中的关键操作,其中 C o n v 1 d ( ⋅ ) Conv1d(·) Conv1d(⋅)在时间维度上执行一维卷积滤波器 ( ( (核宽度 = 3 ) =3) =3),并使用 E L U ( ⋅ ) ELU(·) ELU(⋅)作为激活函数 ( C l e v e r t , U n t e r t h i n e r , a n d H o c h r e i t e r 2016 ) (Clevert, Unterthiner, and\ Hochreiter\ 2016) (Clevert,Unterthiner,and Hochreiter 2016)。我们在堆叠一层后添加一个步长为 2 2 2的最大池化层,将 X t X_t Xt下采样到其一半的切片,这样可以将整个内存使用量减少到 O ( ( 2 − ε ) L l o g L ) O((2 - ε)L log L) O((2−ε)LlogL),其中 ε ε ε是一个很小的数。为了增强蒸馏操作的鲁棒性,我们构建了主堆栈的减半副本,并通过每次丢弃一层来逐渐减少自注意力蒸馏层的数量,形成一个如图所示的金字塔结构,从而使其输出维度对齐。因此,我们将所有堆栈的输出连接起来,得到编码器的最终隐藏表示。
D e c o d e r : Decoder: Decoder:通过一个前向过程生成长序列输出
我们使用的标准解码器结构 V a s w a n i e t a l . 2017 Vaswani\ et\ al. 2017 Vaswani et al.2017,它由两层相同的多头注意力层堆叠而成。然而,为了缓解长预测中速度下降的问题,我们采用了生成式推理。我们将以下向量作为输入提供给解码器:
X feed de t = Concat ( X token t , X 0 t ) ∈ R ( L token + L y ) × d model 方程六 \mathbf{X}{\text{feed de}}^t = \text{Concat}(\mathbf{X}{\text{token}}^t, \mathbf{X}{0}^t) \in \mathbb{R}^{(L{\text{token}} + L_y) \times d_{\text{model}}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 方程六 Xfeed det=Concat(Xtokent,X0t)∈R(Ltoken+Ly)×dmodel 方程六
其中, X t token ∈ R L token × d model X_t^{\text{token}} \in \mathbb{R}^{L_{\text{token}} \times d_{\text{model}}} Xttoken∈RLtoken×dmodel作为起始令牌。 X t 0 Xt_0 Xt0是一个占位符,用于目标序列(将其标量值设为 0 0 0)。在 P r o b S p a r s e ProbSparse ProbSparse自注意力计算中,应用了掩码多头注意力 ( M a s k e d M u l t i − h e a d A t t e n t i o n ) (Masked\ Multi-head\ Attention) (Masked Multi−head Attention),通过将掩码的点积设置为 − ∞ −∞ −∞来阻止每个位置关注到后续位置,从而避免了自回归 ( a u t o − r e g r e s s i v e ) (auto-regressive) (auto−regressive)性质。一个全连接层获取最终输出,其输出大小 d y d_y dy 取决于我们是否执行单变量预测或多变量预测。
生成式推断中的起始令牌是自然语言处理中"动态解码"的一种高效技术,我们将其扩展为生成式的方式。我们并没有选择特定的标志作为令牌,而是在输入序列中采样一个长度为 L t o k e n L_{token} Ltoken的序列,该序列是输出序列之前的一个较早片段。以预测 168 168 168个点为例(即 7 7 7天的温度预测),我们将目标序列之前的已知 5 5 5天作为"起始令牌",并将这些信息与生成式推断解码器一起输入,表示为 X f e e d d e = X 5 d , X 0 X_{feed_de} = {X_{5d}, X_0} Xfeedde=X5d,X0。其中, X 0 X_0 X0包含目标序列的时间戳,即目标周的背景信息。值得注意的是,我们提出的解码器通过一次前向过程即可预测所有输出,避免了传统编码器-解码器架构中耗时的"动态解码"过程。在计算效率部分,我们给出了详细的性能比较。
我们选择均方误差 ( M S E ) (MSE) (MSE)作为预测值与目标序列之间的损失函数,并将损失从解码器的输出反向传播至整个模型。