数据结构--《二叉树》

Peace & Love4872024-06-02 21:26

二叉树

1、什么是二叉树

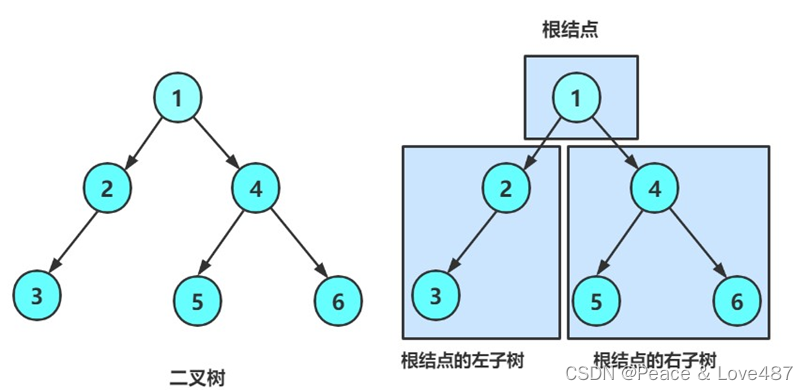
二叉树(Binar Tree)是n(n>=0)个结点的优先集合，该集合或者为空集(称为空二叉树)，或者由一个根结点和两颗互不相交的、分别称为根结点的左子树和右子树的二叉树构成。

这里给张图，能更直观的感受二叉树：

2、二叉树的特点

从上图可以看出二叉树的几个特点：

  1. 二叉树不存在度大于2的结点，每个结点最多有两颗子树；
  2. 左子树和右子树是有顺序的，次序不能颠倒；
  3. 即使树中的某个结点只有一颗子树，那也要区分它是左子树还是右子树。

讲到这那就不得不提及二叉树的五种基本形态：

  1. 空二叉树；
  2. 只有一个根节点；
  3. 根结点只有左子树；
  4. 根结点只有右子树；
  5. 根结点既有左子树又有右子树。

如下图所示，这棵树就不符合二叉树的条件，所以它就不是一颗二叉树。

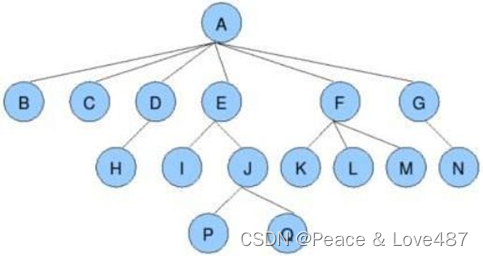
3、几种特殊的二叉树

  1. 斜树 ：顾名思义，斜树一定是要斜的，但是往哪斜是有讲究的。所有结点只有左子树的二叉树叫左斜树。所有结点只有右子树的二叉树叫右斜树。这两者统称为斜树。
  2. 满二叉树 ：在一棵二叉树中，如果所有分支结点都存在左子树和右子树，并且所有叶子都在同一层上，这样的二叉树称为满二叉树。
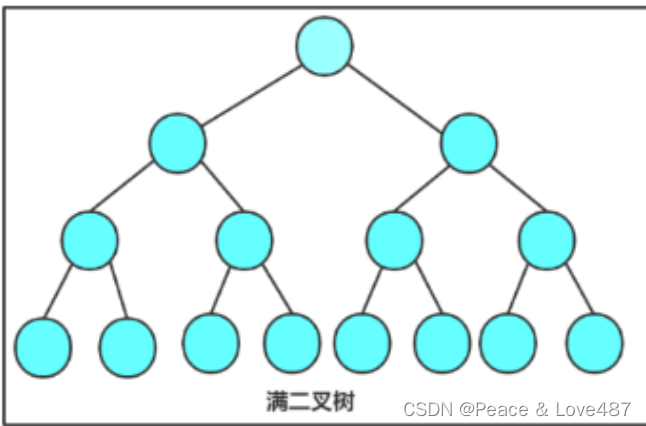
  3. 完全二叉树 ：完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。

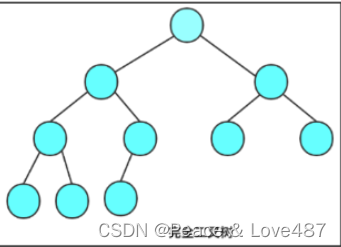
4、二叉树的性质

4.1 满二叉树的性质

  1. 叶子只能出现在最下一层。出现在其他层就不可能达到平衡；
  2. 非叶子节点的度一定是2，否则就是"缺胳膊少腿"了；
  3. 在同样深度的二叉树中，满二叉树的结点个数最多，叶子最多。

4.2 完全二叉树的性质

  1. 叶子结点只能出现在最下两层；
  2. 最下层的叶子一定集中在左部连续位置；
  3. 倒数两层，若有叶子结点，一定都在右部连续位置；
  4. 如果结点度为1，则该结点只有左孩子，即不存在只有右孩子的情况；
  5. 同样结点数的二叉树，完全二叉树的深度最小。

4.3 二叉树的性质

  1. 若规定根节点的层数为 1 ，则一棵非空二叉树的 第 i **层上最多有2^(i-1)**个结点.
  2. 若规定根节点的层数为1，则深度为 h 的二叉树的最大结点数是2^h - 1.
  3. 若规定根节点的层数为 1 ，具有 n 个结点的满二叉树的深度 ， h= log2(n+1). (ps：是log 以 2 为底，n+1 为对数 ).
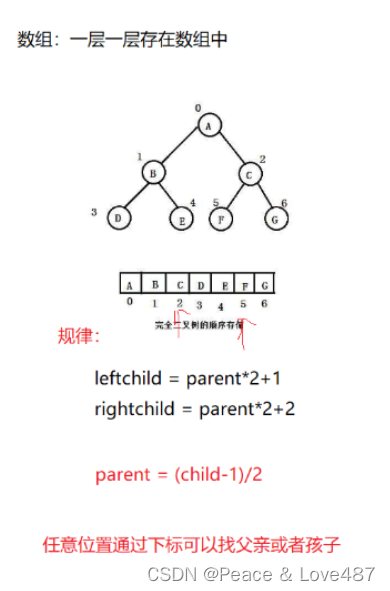
    4. 对于具有n个结点的完全二叉树，如果按照从上至下从左至右的数组顺序对所有节点从0开始编号，则对 于序号为i的结点有：
    1. 若 i>0 ， i 位置节点的双亲序号： (i-1)/2 ； i=0 ， i 为根节点编号，无双亲节点
    2. 若 2i+1<n ，左孩子序号： 2i+1 ， 2i+1>=n 否则无左孩子
    3. 若 2i+2<n ，右孩子序号： 2i+2 ，2i+2>=n否则无右孩子
  4. 对任何一棵二叉树, 如果度为 0 其叶结点个数为n0 , 度为 2 的分支结点个数为n2 , 则有 n0＝n2 ＋ 1.

5、现实中的二叉树

6、二叉树的存储结构

二叉树一般可以使用两种存储结构，一种是顺序存储结构，另一种则是链式存储结构。

6.1 顺序存储结构

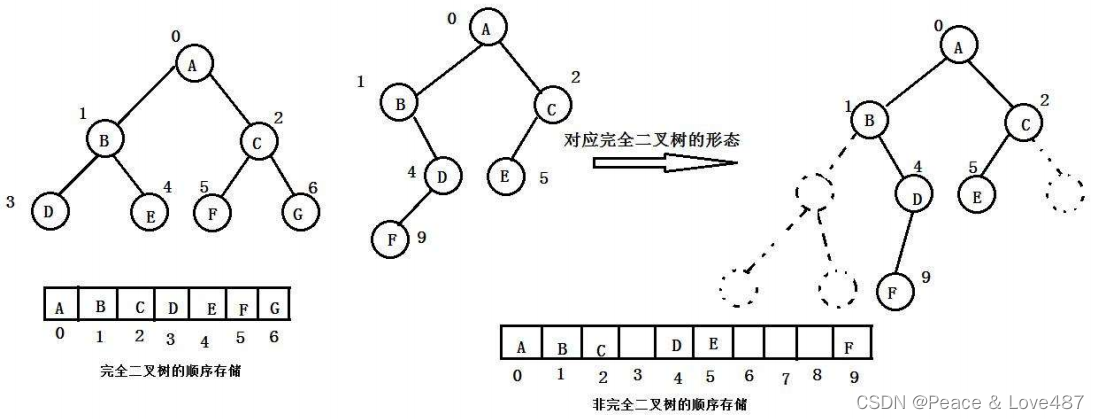
二叉树的顺序存储结构计算用一个一维数组存储二叉树中的结点。一般使用数组只适合表示完全二叉树，因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储。

6.2 链式存储结构

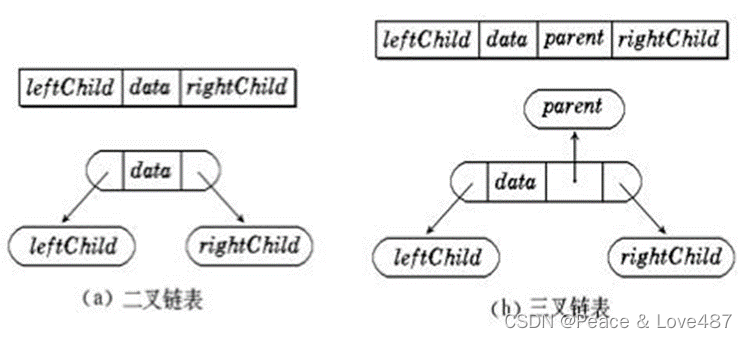
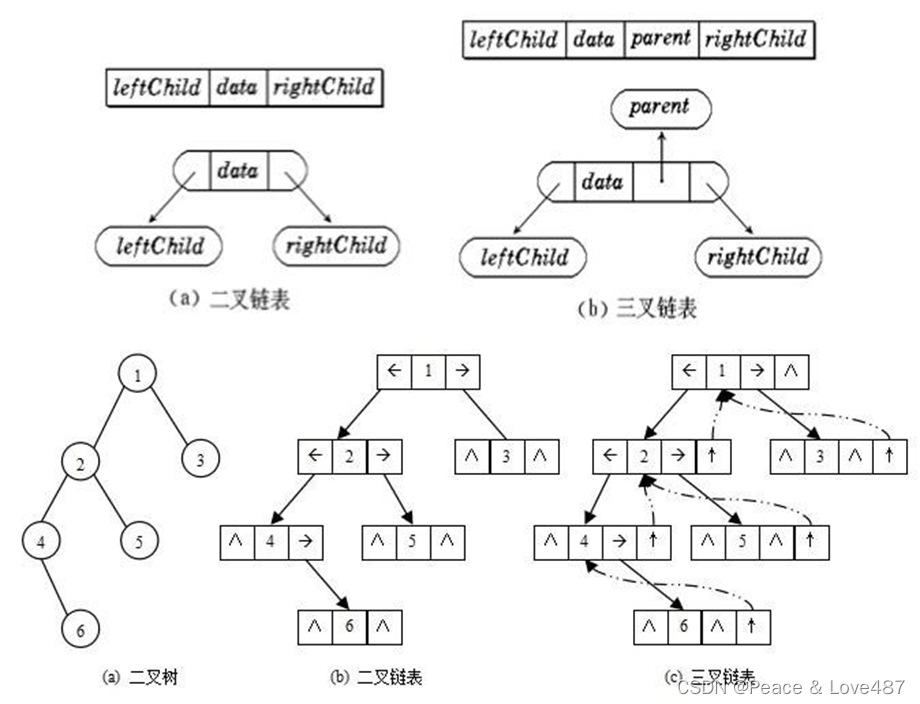
二叉树的链式存储结构是指，用链表来表示一棵二叉树，即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成，数据域和左右指针域，左右指针分别用来给出该结点左孩子和右孩子所 在的链结点的存储地址 。链式结构又分为二叉链和三叉链。

typedef int BTDataType;
// 二叉链
struct BinaryTreeNode
{
 struct BinTreeNode* _pLeft; // 指向当前节点左孩子
 struct BinTreeNode* _pRight; // 指向当前节点右孩子
 BTDataType _data; // 当前节点值域
}
// 三叉链
struct BinaryTreeNode
{
 struct BinTreeNode* _pParent; // 指向当前节点的双亲
 struct BinTreeNode* _pLeft; // 指向当前节点左孩子
 struct BinTreeNode* _pRight; // 指向当前节点右孩子
 BTDataType _data; // 当前节点值域
}；

7、二叉树的顺序存储结构

普通的二叉树是不适合用数组来存储的，因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结 构存储。现实中我们通常把堆 ( 一种二叉树 ) 使用顺序结构的数组来存储，需要注意的是这里的堆和操作系统 虚拟进程地址空间中的堆是两回事，一个是数据结构，一个是操作系统中管理内存的一块区域分段。

7.1 堆的概念和结构

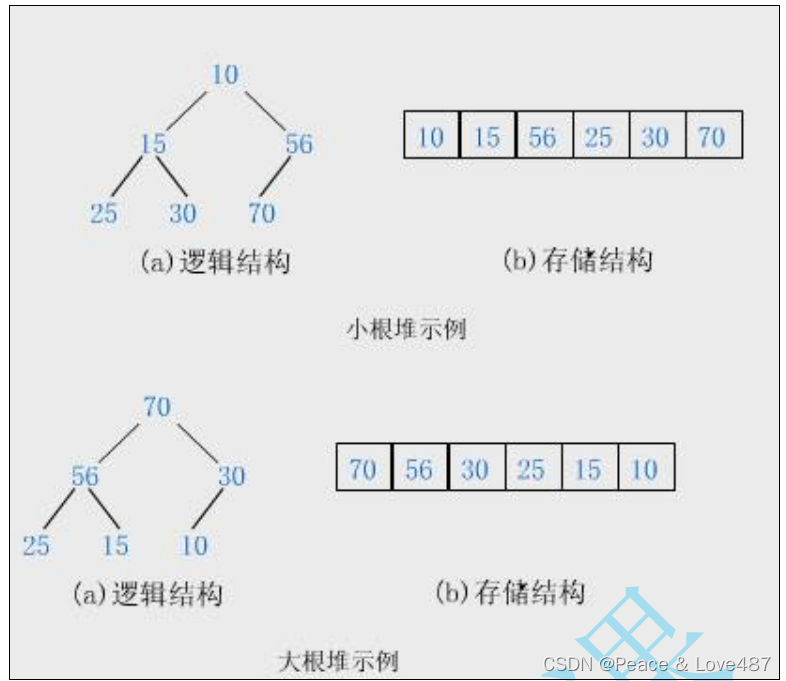
如果有一个关键码的集合 K = { k0 ，k1 ，k2 ， ... ，kn-1}，把它的所有元素按完全二叉树的顺序存储方式存储 在一个一维数组中，并满足： ki<=k2i+2 且 ki<=k2i+1 (ki >=k2i+1 且 ki>=k2i+2 ) i = 0， 1， 2...，则称为小堆 ( 或大堆 ) 。将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。
堆的性质：
堆中某个节点的值总是不大于或不小于其父节点的值；
堆总是一棵完全二叉树。

7.2 堆的实现

实现堆的接口函数：

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
#include<time.h>
#include<string.h>


typedef int HPDataType;
typedef struct Heap
{
	//数组存储
	HPDataType* a;	//数组
	int size;	//数据的个数
	int capacity;	//数组长度
}HP;

//初始化
void HeapInit(HP* php);

//释放空间
void HeapDestory(HP* php);

//插入数据
void HeapPush(HP* php, HPDataType x);

//打印数据
void HeapPrint(HP* php);

//删除数据
void HeapPop(HP* php);

//获取第一个数据
HPDataType HeapTop(HP* php);

//判断是否为空
bool HeapEmpty(HP* php);

函数的具体实现

#define _CRT_SECURE_NO_WARNINGS 1
#include"Heap.h"

//初始化
void HeapInit(HP* php)
{
	assert(php);

	php->a = NULL;
	php->size = php->capacity = 0;
}

//释放空间
void HeapDestory(HP* php)
{
	assert(php);

	free(php->a);
	php->a = NULL;
	php->size = php->capacity = 0;
}

//交换数据
void Swap(HPDataType* x, HPDataType* y)
{
	HPDataType tmp = *x;
	*x = *y;
	*y = tmp;
}

//结点向上调整 -- 小堆
void AdJustUp(HPDataType* a, int child)
{
	int parent = (child - 1) / 2;

	//循环判定条件为孩子结点下标大于0
	while (child > 0)
	{	
		//如果孩子结点值小于父亲节点就相互交换
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (parent - 1) / 2;
		}
		//如果孩子结点值大于或等于父亲节点值就直接跳出循环
		else
		{
			break;
		}
	}

}

//向下调整
void AdJustDown(HPDataType* a, int n, int parent)
{
	int child = 2 * parent + 1;
	
	while (child < n )
	{
		//找出左孩子和右孩子中较小的那个
		if (child+1 < n && a[child + 1] > a[child])
		{
			++child;
		}

		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			//继续向下调整
			parent = child; 
			child = 2 * parent + 1;
		}
		else
		{
			break;
		}
	}
}

//插入数据
void HeapPush(HP* php, HPDataType x)
{
	assert(php);

	//扩容
	if (php->capacity == php->size)
	{
		int newcapacity = php->capacity == 0 ? 4 : 2 * php->capacity;
		HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);
		if (tmp == NULL)
		{
			perror("realloc fail");
			exit(-1);
		}

		php->a = tmp;
		php->capacity = newcapacity;
	}

	php->a[php->size] = x;
	php->size++;

	//插入新元素后，要使原来的堆还是小堆，就得向上调整
	AdJustUp(php->a , php->size-1);
}

//打印数据
void HeapPrint(HP* php)
{
	assert(php);

	for (int i = 0; i < php->size; i++)
	{
		printf("%d ", php->a[i]);
	}
}

//删除数据
void HeapPop(HP* php)
{
	assert(php);
	assert(php->size > 0);

	//交换第一个和最后一个数据
	Swap(&php->a[0], &php->a[php->size - 1]);

	--php->size;

	AdJustDown(php->a, php->size, 0);
}

//获取第一个数据
HPDataType HeapTop(HP* php)
{
	assert(php);
	assert(php->size > 0);

	return php->a[0];
}

//判断是否为空
bool HeapEmpty(HP* php)
{
	assert(php);

	return php->size == 0;
}

8、二叉树的链式存储

8.1、实现链式存储的代码

typedef int BTDataType;
typedef struct BinaryTreeNode
{
 BTDataType _data;
 struct BinaryTreeNode* _left;
 struct BinaryTreeNode* _right;
}BTNode;
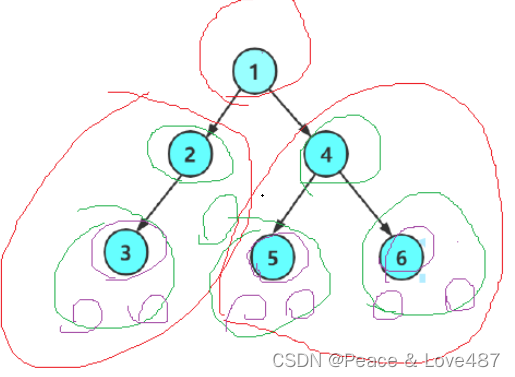
BTNode* CreatBinaryTree()
{
 BTNode* node1 = BuyNode(1);
 BTNode* node2 = BuyNode(2);
 BTNode* node3 = BuyNode(3);

 BTNode* node4 = BuyNode(4);
 BTNode* node5 = BuyNode(5);
 BTNode* node6 = BuyNode(6);
 
 node1->_left = node2;
 node1->_right = node4;
 node2->_left = node3;
 node4->_left = node5;
 node4->_right = node6;
 return node1;
}

9、二叉树的四种遍历方式

9.1、前序遍历

前序遍历(Preorder Traversal 亦称先序遍历)------访问根结点的操作发生在遍历其左右子树之前。

实现前序遍历：

//前序遍历
void PrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}

	printf("%d ", root->val);
	PrevOrder(root->left);
	PrevOrder(root->right);
}

9.2、中序遍历

中序遍历(Inorder Traversal)------访问根结点的操作发生在遍历其左右子树之中（间）。

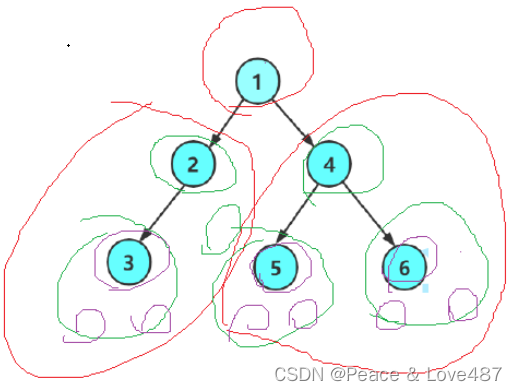
实现中序遍历：

//中序遍历
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}

	InOrder(root->left);
	printf("%d ", root->val);
	InOrder(root->right);
}

9.3、后序遍历

后序遍历(Postorder Traversal)------访问根结点的操作发生在遍历其左右子树之后。

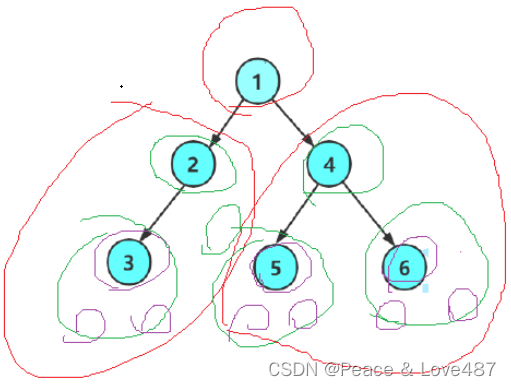
实现后序遍历：

//后序遍历
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}

	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->val);
}

9.4、层序遍历

自上而下，自左至右逐层访问树的结点的过程就是层序遍历。

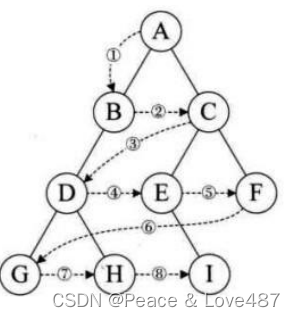
实现层序遍历：

//层序遍历
void LevelOrder(BTNode* root)
{
	if (root == NULL)
		return;

	Que q;
	QueueInit(&q);

	if (root)
	{
		QueuePush(&q, root);
	}

	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		printf("%d ", front->val);

		if (front->left)
		{
			QueuePush(&q, front->left);
		}

		if (front->right)
		{
			QueuePush(&q, front->right);
		}

		QueuePop(&q);
	}
	printf("\n");

	QueueDestroy(&q);
}

由于层序遍历是自下而上一层一层地遍历，所以我们可以用队列(先进先出)来实现这个函数。

相关推荐
盼海1 小时前
排序算法(五)--归并排序
数据结构·算法·排序算法
冰帝海岸5 小时前
01-spring security认证笔记
java·笔记·spring
小二·6 小时前
java基础面试题笔记（基础篇）
java·笔记·python
搬砖的小码农_Sky7 小时前
C语言：数组
c语言·数据结构
先鱼鲨生9 小时前
数据结构——栈、队列
数据结构
一念之坤9 小时前
零基础学Python之数据结构 -- 01篇
数据结构·python
wusong9999 小时前
mongoDB回顾笔记（一）
数据库·笔记·mongodb
猫爪笔记9 小时前
前端：HTML （学习笔记）【1】
前端·笔记·学习·html
Resurgence039 小时前
【计组笔记】习题
笔记
IT 青年9 小时前
数据结构 （1）基本概念和术语
数据结构·算法
热门推荐
01(欧拉)openEuler系统添加网卡文件配置流程、(欧拉)openEuler系统手动配置ipv6地址流程、(欧拉)openEuler系统网络管理说明02PyTorch机器学习实现液态神经网络03【HarmonyOS】HUAWEI DevEco Studio 下载地址汇总04玄机平台应急响应—webshell查杀05Coze扣子平台完整体验和实践（附国内和国际版对比）06Ubuntu 20.04使用Livox mid 360 测试 FAST_LIO07【目标跟踪】相机运动补偿08Unity中PICO实现 隔空取物 和 接触抓取物体09RAG 实践- Ollama+RagFlow 部署本地知识库10怎样让音频速度变慢？请跟随以下方法进行操作