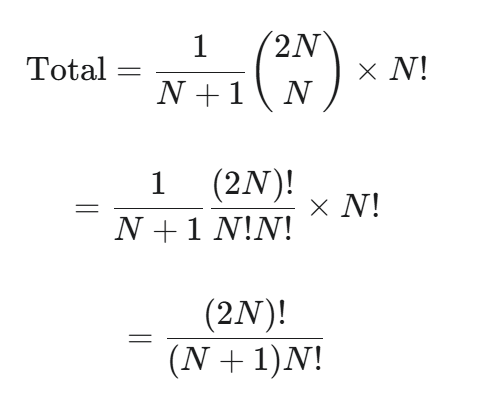目录
[N个无标签节点的二叉树有多少种形态?(Unlabelled N nodes)](#N个无标签节点的二叉树有多少种形态?(Unlabelled N nodes))
[n = 0:](#n = 0:)
[n = 1:](#n = 1:)
[n = 2:](#n = 2:)
[n = 3:](#n = 3:)
[N个有标签节点的二叉树有多少种形态?(Labelled N Nodes)](#N个有标签节点的二叉树有多少种形态?(Labelled N Nodes))
我们将一步步推导拥有 N 个节点的二叉树形态数量。
这里必须先澄清一个核心问题:"节点是否相同?"
1. 无标签节点 (Unlabelled Nodes):所有节点都是一模一样的,我们只关心树的结构。
比如 A(B, C) 和 B(A, C),如果只看结构,它们是不同的(根不同)。
但如果把 A, B, C 三个节点看作是完全一样的"小球",我们只关心能搭出多少种不同的"架子"。
2. 有标签节点 (Labelled Nodes):每个节点都是独一无二的,
比如它们的值是 1, 2, ..., N。在这种情况下,即使两个树的结构完全相同,只要节点上的值(标签)分布不同,它们就是两棵不同的树。
我们先从更根本、也更难的无标签节点问题开始。
N个无标签节点的二叉树有多少种形态?(Unlabelled N nodes)
这个问题本质上是在问:
"用N个一模一样的节点,可以搭出多少种不同的二叉树结构?"
我们设 h(n) 是拥有 n 个节点的二叉树的形态总数。
我们没有现成的公式,所以从最简单的情况开始,寻找规律。
n = 0:
0个节点。有多少种形态?
- 只有一种,那就是空树 (Empty Tree)。所以 h(0)=1
注意:这个基础情况非常重要,是后续所有推导的基石。很多人会误以为是0。但"空树"本身是一种确定的状态。
n = 1:
1个节点。只有一种形态:一个单独的根节点。所以 h(1)=1。
cpp
n=0: ∅
n=1: ●n = 2:
2个节点。我们必须选择一个作为根节点,剩下1个节点。
这1个节点可以是根的左孩子,也可以是根的右孩子。因为二叉树严格区分左右,所以这是两种不同的结构。所以 h(2)=2。
cpp
Case 1: ● Case 2: ●
/ \
● ●n = 3:
3个节点。同样,我们选择一个作为根节点,剩下2个节点需要安排。
这两个节点如何分布在根的左右子树中呢?
cpp
1. ● 2. ● 3. ● 4. ● 5. ●
\ / \ / / \
● ● ● ● ● ●
\ / \ /
● ● ● ●-
情况1: 左子树有2个节点,右子树有0个节点。
-
左子树的2个节点有多少种形态?根据我们上面算出的 h(2),有2种。
-
右子树的0个节点有多少种形态?根据 h(0),有1种(空树)。
-
根据乘法原理,这种情况的总形态数是 h(2) × (0) = 2 种。
-
这个例子里的乘法原理,其实就是组合计数里的一个基本原则:
如果一个结果需要经过 两步(或多步)独立的选择 来确定,并且每一步的选择彼此独立,那么总的可能数 = 各步骤可能数的乘积。
为什么相乘?
-
先选择左子树的形态:有 2 种可能。
-
再选择右子树的形态:有 1 种可能。
这两步是独立的------选了哪一种左子树,并不影响右子树的形状可能性。
-
情况2: 左子树有1个节点,右子树有1个节点。
-
左子树1个节点有 h(1) = 1 种形态。
-
右子树1个节点有 h(1) = 1 种形态。
-
总形态数是 h(1) × (1) = 1 种
-
-
情况3: 左子树有0个节点,右子树有2个节点。
-
左子树0个节点有 h(0) = 1 种形态。
-
右子树2个节点有 h(2) = 2 种形态。
-
总形态数是 h(0) × (2) = 2 种。
-
cpp
Case 1: 左 0,右 2(T(0)×T(2)=1×2 种)
●
\
●
\
●
●
\
●
/
●
Case 2: 左 1,右 1(T(1)×T(1)=1×1 种)
●
/ \
● ●
Case 3: 左 2,右 0(T(2)×T(0)=2×1 种)
●
/
●
\
●
●
/
●
/
●把所有情况加起来,就是 h(3) 的总数:
h(3) = h(2) × (0) +h(1) × (1) + h(0) × (2) = 2 + 1 + 2 = 5 种。
发现规律,建立递推公式
通过 h(3) 的推导,我们发现了一个普适的模式。对于一棵有 n 个节点的树:
-
我们取出一个节点作为根。剩下 n−1 个节点。
-
这 n−1 个节点将被分配到左、右两个子树中。
-
我们可以枚举左子树的节点数量。假设左子树有 i 个节点(i 可以从 0 到 n−1)。
-
那么,右子树就必须有 (n−1)−i 个节点。
-
左子树自身有 h(i) 种形态,右子树自身有 h(n−1−i) 种形态。这两种形态的组合是独立的,所以根据乘法原理,当左子树有 i 个节点时,总的形态数是 h(i)cdoth(n−1−i)。
-
最后,我们把所有可能的 i 的情况(从 i=0 到 i=n−1)全部加起来,就得到了 h(n) 的总数。
这就得到了我们的递推公式:
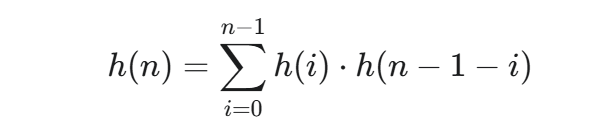
展开来看就是:
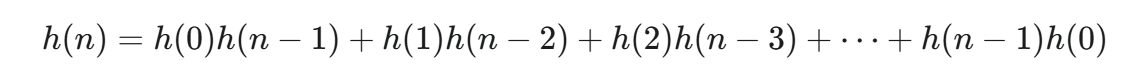
你可能不认识上面这个公式,但在数学领域,这个序列非常非常有名。由这个递推公式定义的序列,就是卡特兰数 (Catalan Number)。
卡特兰数的通项公式 (Closed-Form Formula)
递推公式虽然精确,但每次计算都需要知道前面所有的值,效率很低。
数学家们已经找到了它的通项公式。 (这个通项公式的推导需要用到"生成函数"等高等数学技巧,远超出了数据结构的范畴,所以我们这里不进行第一性推导,而是直接给出结论并解释它。)
卡特兰数的第 n 项(从第0项开始)为:
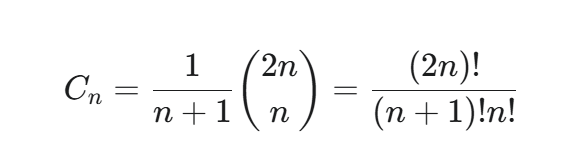
这里 binom2nn 是组合数,读作 "2n choose n",代表从 2n 个不同物品中选出 n 个的方案数。
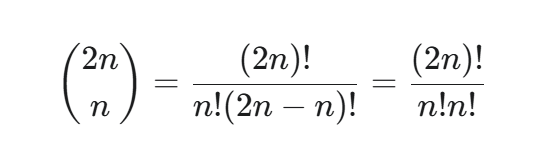
所以,N个无标签节点的二叉树形态数量就是第N个卡特兰数 C_N。
N个有标签节点的二叉树有多少种形态?(Labelled N Nodes)
这个问题比上一个要简单,因为它可以在上一个问题的基础上直接推导。
第一步:选定一个结构
我们已经知道,N个节点能组成的二叉树结构有 C_N 种。
我们先从这 C_N 种结构中随便选出一种。 这个结构有 N 个"空位"(节点位置)。
第二步:给结构贴上标签
现在我们有 N 个不同的标签(比如数字 1, 2, ..., N)。要把这 N 个标签贴到我们选定的那个结构上的 N 个"空位"里。
-
第1个标签,有 N 个位置可以贴。
-
第2个标签,剩下 N−1 个位置可以贴。
-
...
-
最后一个标签,只剩下1个位置。
-
这是一个典型的全排列 (Permutation) 问题。将 N 个不同的标签安排到 N 个不同的位置,总的方案数是 N!
第三步:组合
我们有 C_N 种不同的结构。对于每一种结构,我们都有 N!种不同的贴标签方法。
根据乘法原理,总的形态数就是:
(总形态数) = (结构数) × (每种结构的标签方法数)
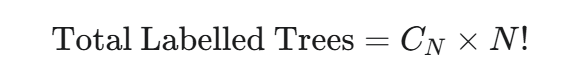
我们把卡特兰数的通项公式代入: