例题1:
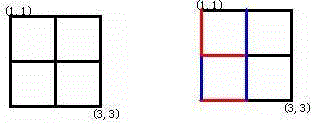
Alice和Bob玩了一个古老的游戏:首先画一个 𝑛×𝑛 的点阵(下图 n=3 )。
接着,他们两个轮流在相邻的点之间画上红边和蓝边:
直到围成一个封闭的圈(面积不必为 1)为止,"封圈"的那个人就是赢家。因为棋盘实在是太大了,他们的游戏实在是太长了!
他们甚至在游戏中都不知道谁赢得了游戏。
于是请你写一个程序,帮助他们计算他们是否结束了游戏?
输入格式
输入数据第一行为两个整数 𝑛 和 𝑚。n𝑛表示点阵的大小,𝑚 表示一共画了 𝑚 条线。
以后 𝑚 行,每行首先有两个数字 (𝑥,𝑦),代表了画线的起点坐标,接着用空格隔开一个字符,假如字符是 𝐷,则是向下连一条边,如果是 R𝑅 就是向右连一条边。
输入数据不会有重复的边且保证正确。
输出格式
输出一行:在第几步的时候结束。
假如 𝑚 步之后也没有结束,则输出一行"draw"。
数据范围
1≤𝑛≤200,
1≤𝑚≤24000
输入样例:
3 5 1 1 D 1 1 R 1 2 D 2 1 R 2 2 D输出样
4
代码:
小细节:二维转一维
cpp
#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<string.h>
#include<algorithm>
#include<cmath>
#include<vector>
#include<queue>
#include<stack>
#include<map>
#include<set>
#include<unordered_map>
#define int long long
using namespace std;
typedef pair<int,int> PII;
const int N = 1e5 + 10;
int n,m,ans;
int p[N];
int get(int x,int y){
return x*n + y;
}
int find(int x){
if(p[x] != x) p[x] = find(p[x]);
return p[x];
}
signed main(){
cin >> n >> m;
for(int i = 0;i < n*n;i ++)
p[i] = i;
for(int i = 1;i <= m;i ++){
int x,y;
char c;
cin >> x >> y >> c;
x --;
y --;
int num1 = get(x,y);
int num2;
if(c == 'D'){
num2 = get(x+1,y);
}
else {
num2 = get(x,y+1);
}
if(find(num1) == find(num2)){
ans = i;
break;
}
p[find(num1)] = find(num2);
}
if(ans) cout << ans ;
else cout << "draw";
return 0;
}例题2:
Joe觉得云朵很美,决定去山上的商店买一些云朵。
商店里有 n 朵云,云朵被编号为 1,2,...,n,并且每朵云都有一个价值。
但是商店老板跟他说,一些云朵要搭配来买才好,所以买一朵云则与这朵云有搭配的云都要买。
但是Joe的钱有限,所以他希望买的价值越多越好。
输入格式
第 11 行包含三个整数 n,m,w,表示有 n 朵云,m 个搭配,Joe有 𝑤 的钱。
第 2∼n+1行,每行两个整数 ci,di表示 i 朵云的价钱和价值。
第 n+2∼n+1+m 行,每行两个整数 ui,vi表示买 ui 就必须买 v𝑖,同理,如果买 vi就必须买 ui。
输出格式
一行,表示可以获得的最大价值。
数据范围
1≤𝑛≤10000,
0≤𝑚≤5000,
1≤𝑤≤10000,
1≤𝑐𝑖≤5000,
1≤𝑑𝑖≤100,
1≤𝑢𝑖,𝑣𝑖≤𝑛
输入样例:
5 3 10 3 10 3 10 3 10 5 100 10 1 1 3 3 2 4 2输出样例:
1
代码:01背包
cpp
#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<string.h>
#include<algorithm>
#include<cmath>
#include<vector>
#include<queue>
#include<stack>
#include<map>
#include<set>
#include<unordered_map>
#define int long long
using namespace std;
typedef pair<int,int> PII;
const int N = 1e5 + 10;
int n,m,sum;
int v[N],w[N],p[N];
int dp[N];
int find(int x){
if(p[x] != x) p[x] = find(p[x]);
return p[x];
}
signed main(){
cin >> n >> m >> sum;
for(int i = 1;i <= n;i ++)
p[i] = i;
for(int i = 1;i <= n;i ++)
cin >> v[i] >> w[i];
while(m --){
int a,b;
cin >> a >> b;
int num1 = find(p[a]);
int num2 = find(p[b]);
if(num1 != num2){
v[num2] += v[num1];
w[num2] += w[num1];
p[num1] = num2;
}
}
for(int i = 1;i <= n;i ++){
if(p[i] == i)
for(int j = sum;j >= v[i];j --)
dp[j] = max(dp[j],dp[j-v[i]]+w[i]);
}
cout << dp[sum];
return 0;
}例题3:
在实现程序自动分析的过程中,常常需要判定一些约束条件是否能被同时满足。
考虑一个约束满足问题的简化版本:假设 𝑥1,𝑥2,𝑥3,... 代表程序中出现的变量,给定 𝑛 个形如 xi=xj𝑥𝑖=𝑥𝑗 或 xi≠xj𝑥𝑖≠𝑥𝑗 的变量相等/不等的约束条件,请判定是否可以分别为每一个变量赋予恰当的值,使得上述所有约束条件同时被满足。
例如,一个问题中的约束条件为:𝑥1=𝑥2,𝑥2=𝑥3,𝑥3=𝑥4,𝑥1≠𝑥4,这些约束条件显然是不可能同时被满足的,因此这个问题应判定为不可被满足。
现在给出一些约束满足问题,请分别对它们进行判定。
输入格式
输入文件的第 1行包含 1 个正整数 t𝑡,表示需要判定的问题个数,注意这些问题之间是相互独立的。
对于每个问题,包含若干行:
第 1 行包含 1 个正整数 n,表示该问题中需要被满足的约束条件个数。
接下来 n 行,每行包括 33个整数 i,j,e,描述 1个相等/不等的约束条件,相邻整数之间用单个空格隔开。若 e=1,则该约束条件为 xi=xj;若 e=0,则该约束条件为 xi≠xj。
输出格式
输出文件包括 𝑡 行。
输出文件的第 𝑘 行输出一个字符串
YES或者NO,YES表示输入中的第 𝑘 个问题判定为可以被满足,NO表示不可被满足。数据范围
1≤t≤10
1≤n≤10^5
1≤i,j≤10^9
输入样例:
2 2 1 2 1 1 2 0 2 1 2 1 2 1 1输出样例:
NO YES
代码:(离散化+并查集)
cpp
#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<string.h>
#include<algorithm>
#include<cmath>
#include<vector>
#include<queue>
#include<stack>
#include<map>
#include<set>
#include<unordered_map>
#define int long long
using namespace std;
typedef pair<int,int> PII;
const int N = 2e5 + 10;
int T,n,cnt;
unordered_map<int,int> m;
struct NODE{
int i,j,e;
}node[N];
int p[N];
int get(int x){
if(m.count(x) == 0)
m[x] = ++cnt;
return m[x];
}
int find(int x){
if(x != p[x])
p[x] = find(p[x]);
return p[x];
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> T;
while(T --){
cnt = 0;
m.clear();
cin >> n;
for(int i = 0;i < n;i ++){
cin >> node[i].i >> node[i].j >> node[i].e;
node[i].i = get(node[i].i);
node[i].j = get(node[i].j);
}
for(int i = 1;i <= cnt;i ++){
p[i] = i;
}
for(int i = 0;i < n;i ++){
if(node[i].e == 1){
int num1 = find(node[i].i);
int num2 = find(node[i].j);
p[num2] = num1;
}
}
bool flag = false;
for(int i = 0;i < n;i ++){
if(node[i].e == 0){
int num1 = find(node[i].i);
int num2 = find(node[i].j);
if(num1 == num2){
flag = true;
break;
}
}
}
if(flag) cout << "NO" << '\n';
else cout << "YES" << '\n';
}
return 0;
}