前言
随着能源问题日益突出,风力发电等以可再生能源为基础的发电技术越来越受到关注。建立能够正确反映实际风速特性的风速模型是研究风力发电系统控制策略以及并网运行特性的重要基础叫。由于风速的随机性和波动性,系统中的机械设备和电气设备以及电网均会受到扰动,这种扰动对于系统设备的寿命、运行性能以及电网的稳定性都将产生一定的影响。因而,在研究风电场接入电网的功率波动与电能质量等动态特性时,需要建立与之相适应的风速模型。
ARMA模型
自回归滑动平均模型(Auto-Regressive and Moving Average ,ARMA)是研究时间序列的重要方法,已广泛应用于经济学、股票、期货等领域当中。其原理是利用已知的信号序列、误差以及已知序列对信号自身的影响规律来预测未来的信号序列。ARMA模型描述了离散随机信号中各序列之间的依存关系。ARMA模型具有以下特征:
1)以线性差分方程描述离散随机信号序列;
2)任何一个有理式的功率谱都可以用一个ARMA随机过程的功率密度谱精确逼近;
3)ARMA模型满足Yule-Walker方程;
两参数Weibull分布
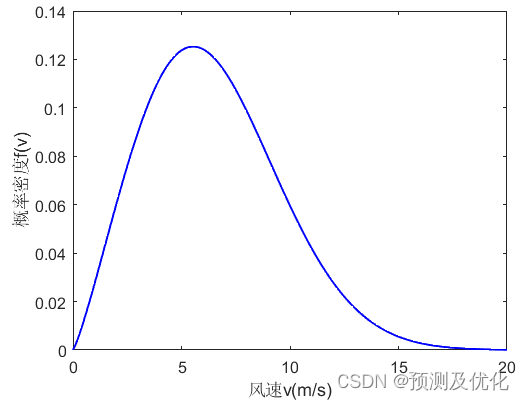
两参数的Weibull分布模型是适用范围最广、拟合实际风速最好的模型,它能调整参数来适应不同时间长度(通常是一个月或一年)的风速序列。在风速和风能评估方面已有很多应用。
两参数的Weibull分布的概率密度函数如下式所示:
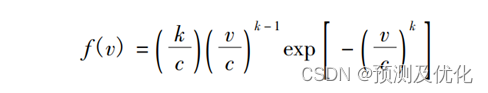
其分布函数如下式所示:
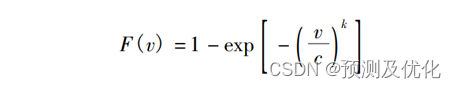
程序介绍
自回归滑动平均模型(ARMA)是分析时间序列的重要方法。在分析实际风速统计特性和ARMA模型性质的基础上,建立了可用于动态仿真的短期风速模型。程序结果表明,所得风速序列能够正确反映实际风速的特性。在风能领域Weibul分布常用于描述风速的分布特征,通过拟合Weibull分布可以得到风速的概率密度分布,为风能资源的评估和风电场的布局提供重要依据。程序中算例丰富,注释清晰,干货满满,创新性和可扩展性很高,下面对程序做简要介绍!
程序结果
ARMA模型结果
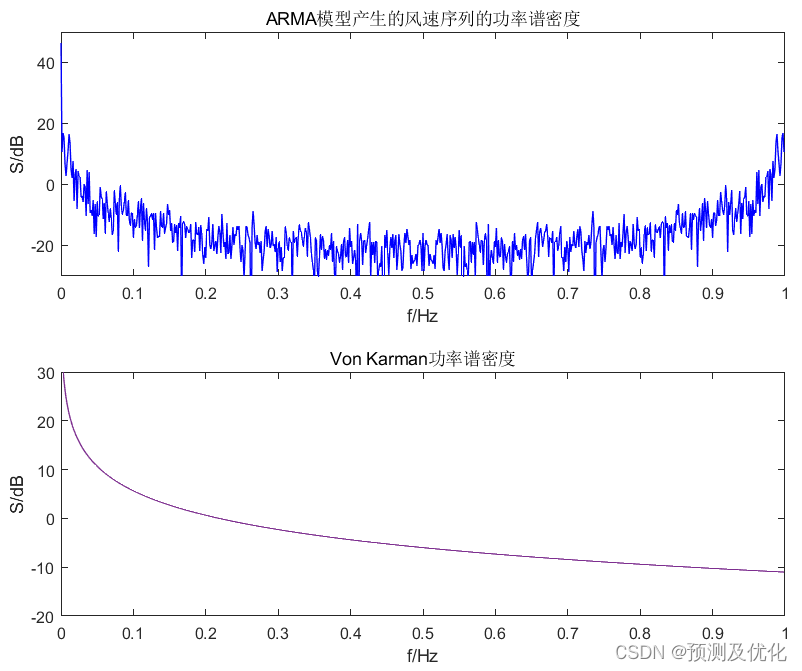
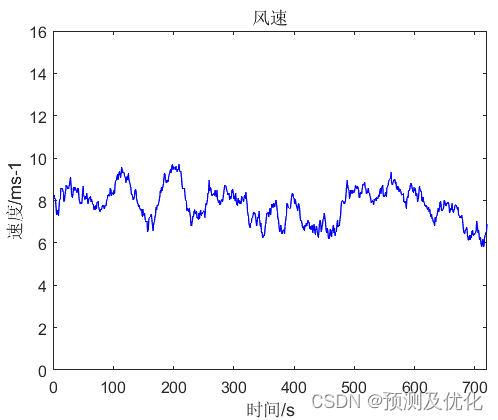
风速Weibull分布结果
部分程序
Matlab
%初始化
I=0.16;%湍流强度L=600;%湍流尺度
average_v=8.11850232757234;%平均风速
Ts=1;%采样时间T=720;%模拟时间n=T/Ts;%采样个数
sigma_u=3.48648820169842;%风速序列的标准差
sigma_noise=0.2;%白噪声的方差
% u=yyx_noice_n(0,sigma_noise,n);%产生n个序列的白噪声,均值为0,方差为1;
u=normrnd(0,sigma_noise,n);df=1/T;%频率分辨率
f=(0:n-1)*df;length_f=length(f);
S(i)=4*(sigma_u)^2*L/average_v/(1+70.8*(f(i)*L/average_v)^2)^(5/6);%Von Karman谱功率密度函数
R=real(ifft(S));%自相关与功率谱密度是傅立叶变换关系,求自相关
%求解AR模型参数
a(1)=R(2)/R(1);a(2)=R(3)/R(1)-R(2)*R(2)/R(1)/R(1);
%求解MA模型参数
Ry=(-a(1)+a(2)*a(1))*R(1)+(1+a(1)^2+a(2)^2)*R(2)+(-a(1)+a(1)*a(2))*R(3)+(-a(2))*R(4);
b=Ry/sigma_noise;%beta=Ry/白噪声的方差
%脉动风速
v(1)=u(1);v(2)=a(1)*v(1)+u(2)+b*u(1);
v(k)=a(1)*v(k-1)+a(2)*v(k-2)+u(k)+b*u(k-1);%ARMA模型部分内容源自网络,侵权联系删除!
欢迎感兴趣的关注并私信获取完整版代码,小编会不定期更新高质量的学习资料、文章和程序代码,为您的科研加油助力!