目录
主要内容
程序主要内容是考虑风光场景生成的电动汽车并网优化调度,采用的方法如下所述:
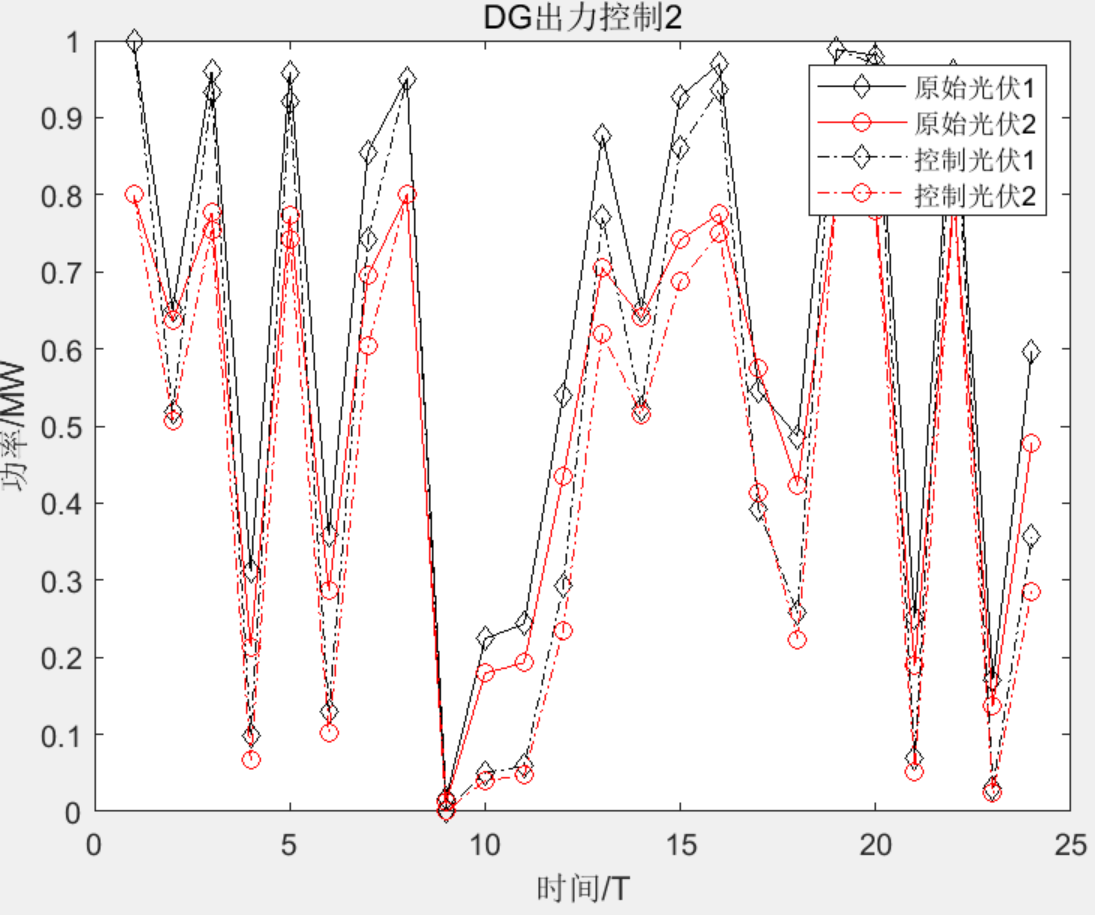
①采用蒙特卡洛方法,结合copula函数以及fuzzy-kmeans,获取6个典型风光出力场景,并进行随机优化调度。
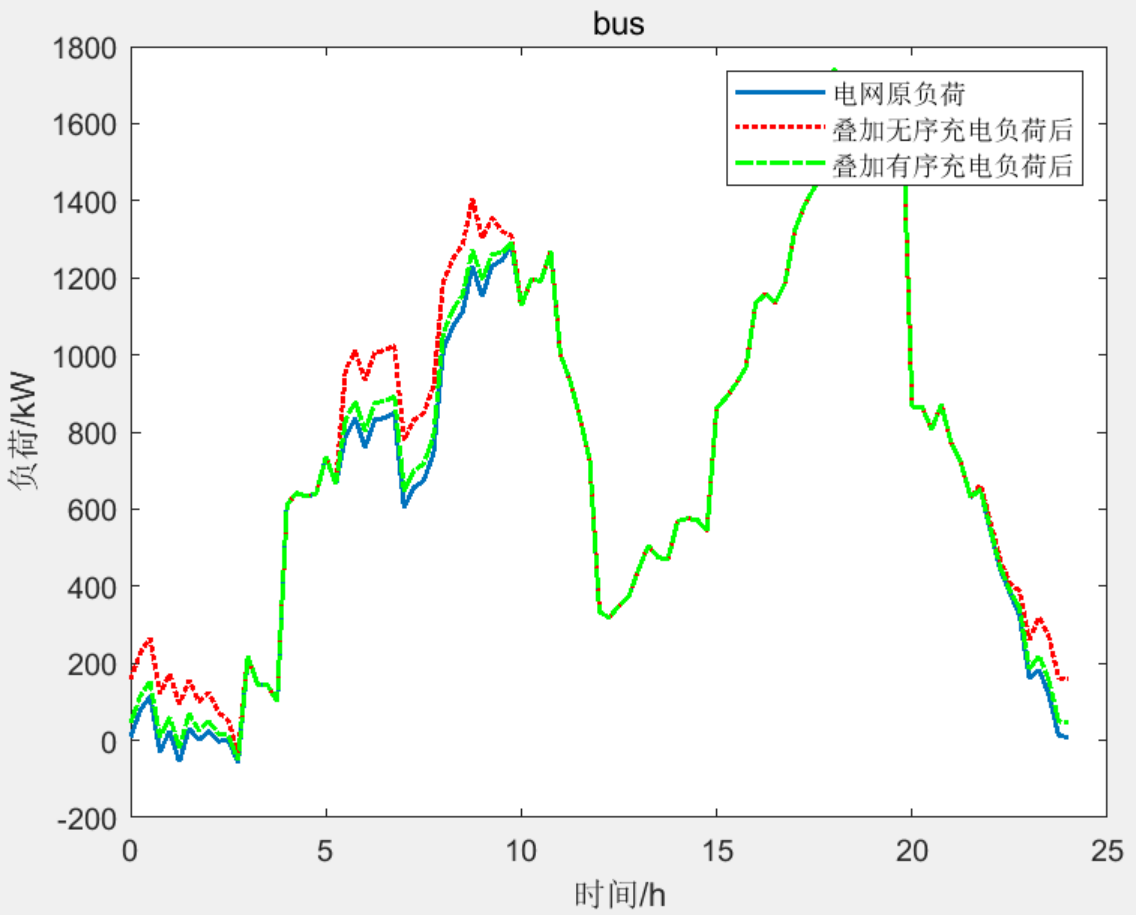
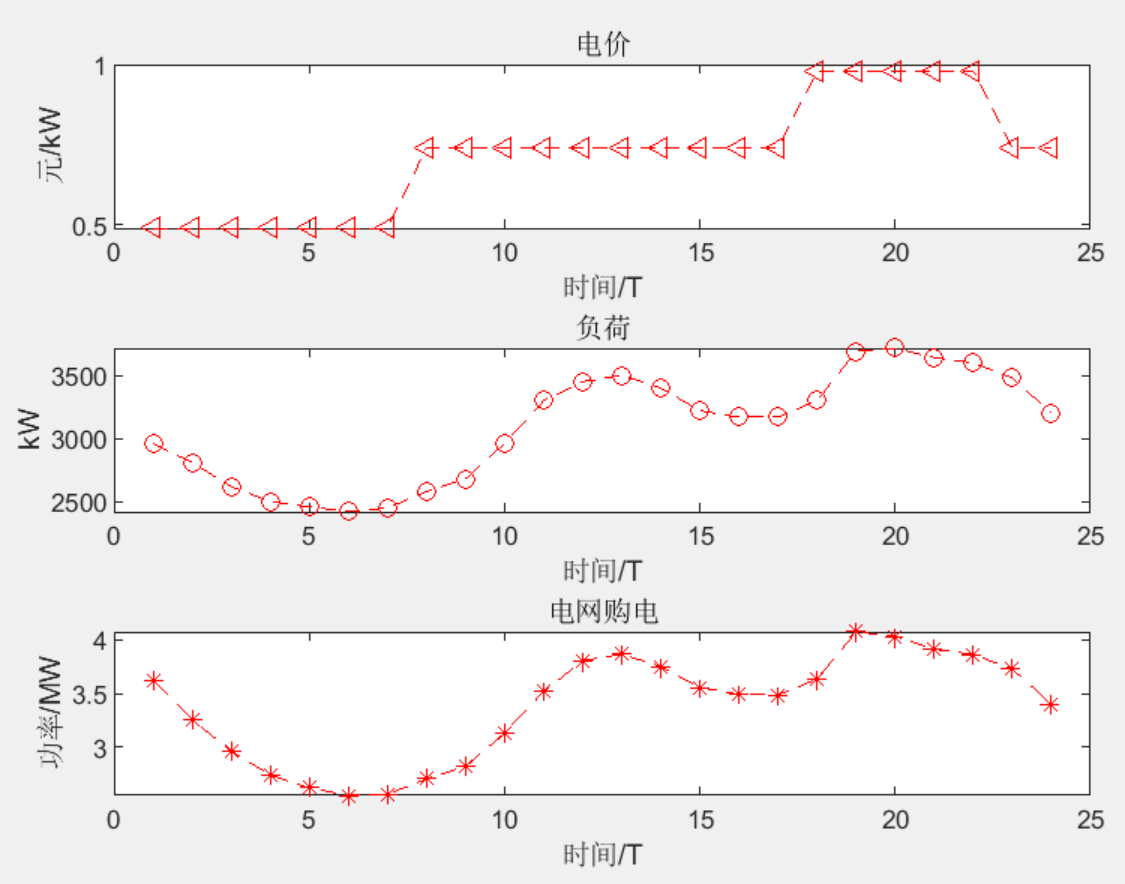
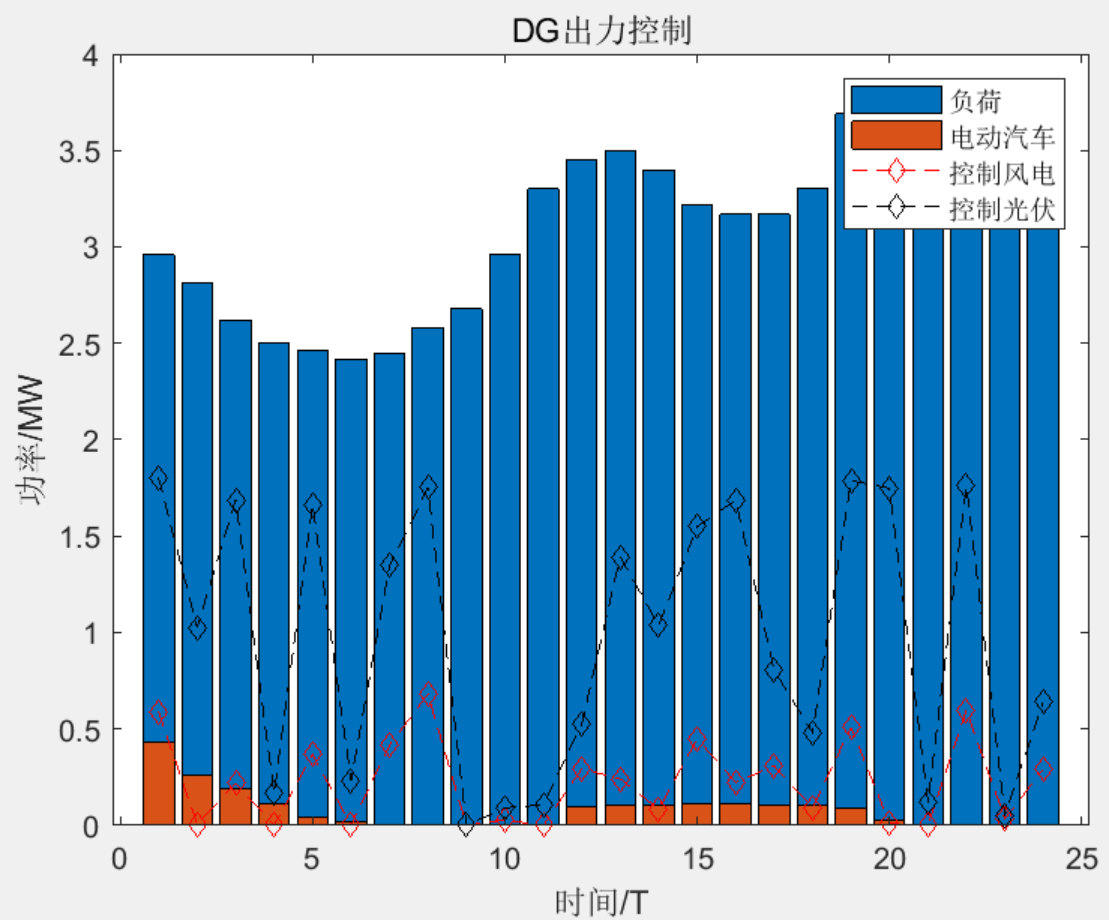
②考虑多类型电动汽车,包括出租、商用、公交和家庭用车,电价采用分时电价,目标函数考虑上级电网出力、峰谷差惩罚费用、风光调度、电动汽车负荷调度费用和网损费用。
③通过IEEE33节点系统中进行仿真算例分析,程序中增加电压约束限制,保证电动汽车优化调度的同时33节点系统电压维持在合理水平。
部分代码
SOC=SOC-judge;
battery=SOC*Cbattery; %到班后的电量
time1=zeros(1,Ntest); %初始化时间点为0
time2=zeros(1,Ntest);
%SOC记录数组
SOC_sa=ones(1,Ntest); %初始化SOC为1
SOC_sb=ones(1,Ntest);
for i=1:Ntest
if SOC(i)0.2
SOC_sa(i)=SOC(i);
time1(i)=timework(i); %到班后需要充电,充电开始时间为到班时间
time2(i)=time1(i)+(1-SOC(i))*Cbattery/Pcharge; %充电结束时间,充电功率Pcharge
SOC(i)=SOC_end; %下班前充满电
battery(i)=Cbattery*SOC(i);
end
end
SOC=SOC-judge;
battery=SOC*Cbattery; %到家后的电量
time3=zeros(1,Ntest);
time4=zeros(1,Ntest);
for i=1:Ntest
if SOC(i)0.4)
SOC_sb(i)=SOC(i);
time3(i)=timehome(i); %到家后需要充电,充电开始时间为到班时间
time4(i)=time3(i)+(1-SOC(i))*Cbattery/Pcharge; %充电结束时间,充电功率4KW
SOC(i)=SOC_end; %第二天8点前可以充满电
battery(i)=Cbattery*SOC(i);
end
end
time=0:0.1:48;
Ycharge=zeros(1,481);
roundn(time1,-1);
roundn(time2,-1);
roundn(time3,-1);
roundn(time4,-1);
for i=1:Ntest %找到所有充电车辆的电量
if (time2(i)-time1(i)~=0)
kstart=round(10*time1(i)+1);
kend=round(10*time2(i)+1);
Ycharge(1,kstart:kend)=Ycharge(1,kstart:kend)+1;
end
if (time4(i)-time3(i)~=0)
kstart=round(10*time3(i)+1);
kend=round(10*time4(i)+1);
Ycharge(1,kstart:kend)=Ycharge(1,kstart:kend)+1;
end
end
temp=Ycharge(1:241)+Ycharge(241:481);
x=0:0.1:24;
xx=0:0.05:24;
tempp = interp1(x,temp,xx,'linear'); %现性插值
Pwuxu=tempp(1:5:481)*Pbiao;%充电功率为15kW
price=zeros(1,96);
price(1,18*4:22*4)=0.98;
price(1,8*4:17*4)=0.74;price(1,23:24)=0.74;
price(1,1:7*4)=0.49;
%=========================================================================
%解有序充电模型
deltaT=15/60;%15min折算成小时(根据电网数据采集)
cost=0;%购电电价部分结果