目录
[1 主要内容](#1 主要内容)
[2 部分代码](#2 部分代码)
[3 程序结果](#3 程序结果)
[4 下载链接](#4 下载链接)
1 主要内容
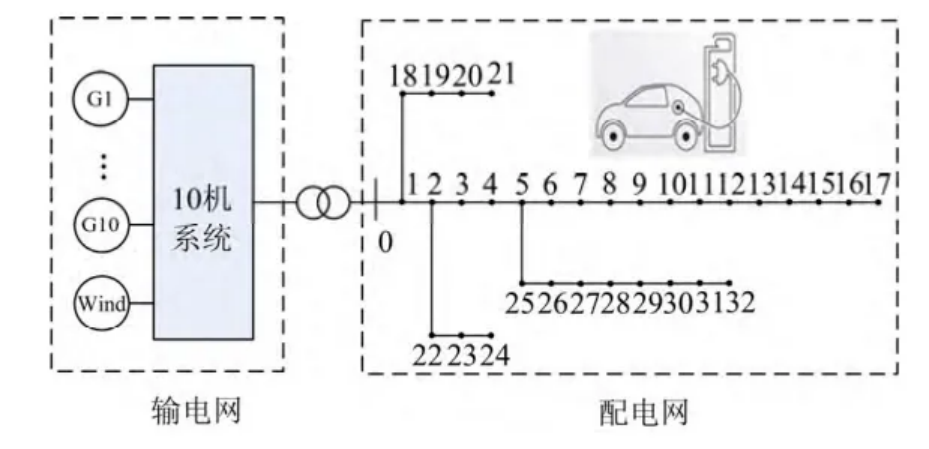
该程序复现文章《A bi-layer optimization based temporal and spatial scheduling for large-scale electric vehicles》,中文文献可对照《考虑大规模电动汽车接入电网的双层优化调度策略》,研究了发电机、电动汽车、风力的协同优化计划问题,提出了一种基于输电和配电系统层面的电动汽车充放电计划双层优化调度策略。在输电网层,以减少发电机组的运行成本、PM2.5 排放量、用户的总充电成本和弃风电量为目标,建立了基于机组最优组合的上层优化调度模型;在配电网层,以降低网损为目标,考虑网络安全约束和电动汽车的空间迁移特性,建立了基于最优潮流的下层优化调度模型。在基于标准 10 机输电网和 IEEE33 节点配电网的电力系统仿真模型上,对所提的基于双层优化的大规模电动汽车充放电调度策略进行了仿真分析,验证了所提双层优化调度策略的有效性和优越性。
由于该程序整体运行时间比较长,为了方便大家学习,采用上下层分别独立运行的方式,有兴趣的同学可以将两部分结合一下,但是运行时间会比较长,占用内存较大,程序采用matlab+cplex求解。为了方便大家学习,我对代码进行了比较详细的注释,希望能帮助到各位。


这个程序思路不难,上层和参考文献一致未考虑输电网节点,重难点就是线性化处理部分,采用分段线性化的方式,下层主要设置电动汽车充放电数量,电动汽车充放电功率是固定的,然后将电动汽车功率带入到配电网潮流、电压和二阶锥等约束中,计算出电动汽车不同时间段充放电数量,这个程序有个优势,采用不同的配网优化方式,我们之前配网二阶锥优化采用的是下述形式。

简单来说就是,需要定义电压平方、电流平方、有功、无功等变量,该程序采用的变量如下:
u=sdpvar(32,1);%u=Volta^2;电压平方变量
R=sdpvar(32,1);%R=Volta(i)*Volta(j)*cos(Theta(i)-Theta(j));
T=sdpvar(32,1);%T=Volta(i)*Volta(j)*sin(Theta(i)-Theta(j));
Nd=intvar(32,1);%放电电动汽车数量
Nc=intvar(32,1);%充电电动汽车数量该方式直接定义了相连节点电压与cos(或者sin)乘积非线性部分作为一个整体变量,因此约束形式和常规二阶锥优化也会存在差异。
- 上层目标函数

- 下层目标函数
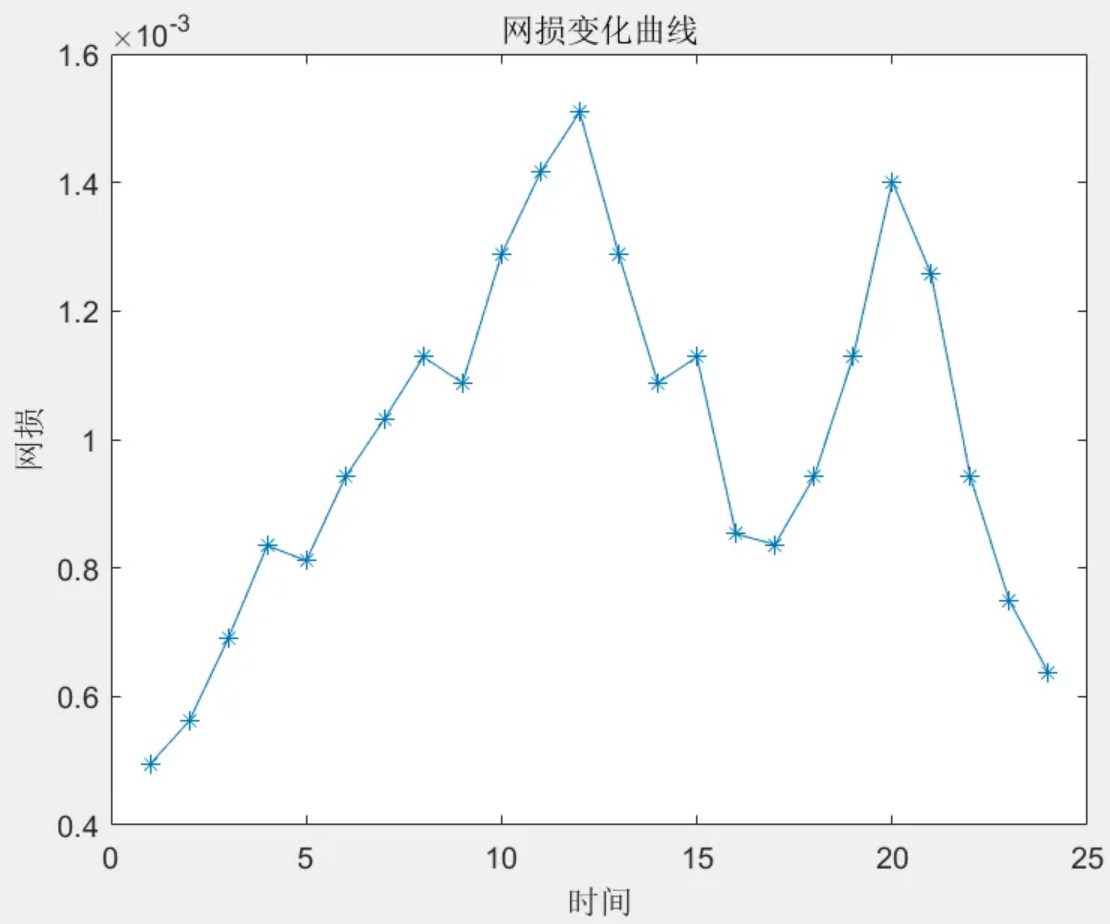
网损最小

- 下层约束条件

2 部分代码
%%%%%%配电网潮流优化%%%%%%%%
%%%%%%标幺值SB=100MVA,UB=12.66kV,二阶锥松弛%%%%%%
%%%%%%MISOCP模型,分时段优化,并行计算%%%%%%%%%%%%
clear
clc
%%%%%IEEE33配电网数据%%%%%%%%%%%;
%有功、无功数据
Pload=[0.0004666666667,0.0005,0.0005666666667,0.0006333333333,0.0006666666667,0.0007333333333;
Qload=[0.00028,0.0003,0.00034,0.00038,0.0004,0.00044,0.00046,0.00048,0.00052,0.00056,0.00058,0.0006,0.00056,0.00052,0.00048,0.00042,0.0004,0.00044,0.00048,0.00056,0.00052,0.00044,0.00036,0.00032;0.0001866666667,0.0002,0.0002266666667,0.0002533333333,0.0002666666667,0.0002933333333,0.0003066666667,0.00032,0.0003466666667,0.0003733333333,0.0003866666667,0.0004,0.0003733333333,0.0003466666667,0.00032,0.00028,0.0002666666667,0.0002933333333,0.00032,0.0003733333333,0.0003466666667,0.0002933333333,0.00024,0.0002133333333;0.0003733333333,0.0004,0.0004533333333,0.0005066666667,0.0005333333333,0.0005866666667,0.0006133333333,0.00064,0.0006933333333,0.0007466666667,0.0007733333333,0.0008,0.0007466666667,0.0006933333333,0.00064,0.00056,0.0005333333333,0.0005866666667,0.00064,0.0007466666667,0.0006933333333,0.0005866666667,0.00048,0.0004266666667;0.00014,0.00015,0.00017,0.00019,0.0002,0.00022,0.00023,0.00024,0.00026,0.00028,0.00029,0.0003,0.00028,0.00026,0.00024,0.00021,0.0002,0.00022,0.00024,0.00028,0.00026,0.00022,0.00018,0.00016;9.333333333e-05,0.0001,0.0001133333333,0.0001266666667,0.0001333333333,0.0001466666667,0.0001533333333,0.00016,0.0001733333333,0.0001866666667,0.0001933333333,0.0002,0.0001866666667,0.0001733333333,0.00016,0.00014,0.0001333333333,0.0001466666667,0.00016,0.0001866666667,0.0001733333333,0.0001466666667,0.00012,0.0001066666667;0.0004666666667,0.0005,0.0005666666667,0.0006333333333,0.0006666666667,0.0007333333333,0.0007666666667,0.0008,0.0008666666667,0.0009333333333,0.0009666666667,0.001,0.0009333333333,0.0008666666667,0.0008,0.0007,0.0006666666667,0.0007333333333,0.0008,0.0009333333333,0.0008666666667,0.0007333333333,0.0006,0.0005333333333;0.0004666666667,0.0005,0.0005666666667,0.0006333333333,0.0006666666667,0.0007333333333,0.0007666666667,0.0008,0.0008666666667,0.0009333333333,0.0009666666667,0.001,0.0009333333333,0.0008666666667,0.0008,0.0007,0.0006666666667,0.0007333333333,0.0008,0.0009333333333,0.0008666666667,0.0007333333333,0.0006,0.0005333333333;9.333333333e-05,0.0001,0.0001133333333,0.0001266666667,0.0001333333333,0.0001466666667,0.0001533333333,0.00016,0.0001733333333,0.0001866666667,0.0001933333333,0.0002,0.0001866666667,0.0001733333333,0.00016,0.00014,0.0001333333333,0.0001466666667,0.00016,0.0001866666667,0.0001733333333,0.0001466666667,0.00012,0.0001066666667;9.333333333e-05,0.0001,0.0001133333333,0.0001266666667,0.0001333333333,0.0001466666667,0.0001533333333,0.00016,0.0001733333333,0.0001866666667,0.0001933333333,0.0002,0.0001866666667,0.0001733333333,0.00016,0.00014,0.0001333333333,0.0001466666667,0.00016,0.0001866666667,0.0001733333333,0.0001466666667,0.00012,0.0001066666667;0.00014,0.00015,0.00017,0.00019,0.0002,0.00022,0.00023,0.00024,0.00026,0.00028,0.00029,0.0003,0.00028,0.00026,0.00024,0.00021,0.0002,0.00022,0.00024,0.00028,0.00026,0.00022,0.00018,0.00016;0.0001633333333,0.000175,0.0001983333333,0.0002216666667,0.0002333333333,0.0002566666667,0.0002683333333,0.00028,0.0003033333333,0.0003266666667,0.0003383333333,0.00035,0.0003266666667,0.0003033333333,0.00028,0.000245,0.0002333333333,0.0002566666667,0.00028,0.0003266666667,0.0003033333333,0.0002566666667,0.00021,0.0001866666667;0.0001633333333,0.000175,0.0001983333333,0.0002216666667,0.0002333333333,0.0002566666667,0.0002683333333,0.00028,0.0003033333333,0.0003266666667,0.0003383333333,0.00035,0.0003266666667,0.0003033333333,0.00028,0.000245,0.0002333333333,0.0002566666667,0.00028,0.0003266666667,0.0003033333333,0.0002566666667,0.00021,0.0001866666667;0.0003733333333,0.0004,0.0004533333333,0.0005066666667,0.0005333333333,0.0005866666667,0.0006133333333,0.00064,0.0006933333333,0.0007466666667,0.0007733333333,0.0008,0.0007466666667,0.0006933333333,0.00064,0.00056,0.0005333333333,0.0005866666667,0.00064,0.0007466666667,0.0006933333333,0.0005866666667,0.00048,0.0004266666667;4.666666667e-05,5.e-05,5.666666667e-05,6.333333333e-05,6.666666667e-05,7.333333333e-05,7.666666667e-05,8.e-05,8.666666667e-05,9.333333333e-05,9.666666667e-05,0.0001,9.333333333e-05,8.666666667e-05,8.e-05,7.e-05,6.666666667e-05,7.333333333e-05,8.e-05,9.333333333e-05,8.666666667e-05,7.333333333e-05,6.e-05,5.333333333e-05;9.333333333e-05,0.0001,0.0001133333333,0.0001266666667,0.0001333333333,0.0001466666667,0.0001533333333,0.00016,0.0001733333333,0.0001866666667,0.0001933333333,0.0002,0.0001866666667,0.0001733333333,0.00016,0.00014,0.0001333333333,0.0001466666667,0.00016,0.0001866666667,0.0001733333333,0.0001466666667,0.00012,0.0001066666667;9.333333333e-05,0.0001,0.0001133333333,0.0001266666667,0.0001333333333,0.0001466666667,0.0001533333333,0.00016,0.0001733333333,0.0001866666667,0.0001933333333,0.0002,0.0001866666667,0.0001733333333,0.00016,0.00014,0.0001333333333,0.0001466666667,0.00016,0.0001866666667,0.0001733333333,0.0001466666667,0.00012,0.0001066666667;0.0001866666667,0.0002,0.0002266666667,0.0002533333333,0.0002666666667,0.0002933333333,0.0003066666667,0.00032,0.0003466666667,0.0003733333333,0.0003866666667,0.0004,0.0003733333333,0.0003466666667,0.00032,0.00028,0.0002666666667,0.0002933333333,0.00032,0.0003733333333,0.0003466666667,0.0002933333333,0.00024,0.0002133333333;0.0001866666667,0.0002,0.0002266666667,0.0002533333333,0.0002666666667,0.0002933333333,0.0003066666667,0.00032,0.0003466666667,0.0003733333333,0.0003866666667,0.0004,0.0003733333333,0.0003466666667,0.00032,0.00028,0.0002666666667,0.0002933333333,0.00032,0.0003733333333,0.0003466666667,0.0002933333333,0.00024,0.0002133333333;0.0001866666667,0.0002,0.0002266666667,0.0002533333333,0.0002666666667,0.0002933333333,0.0003066666667,0.00032,0.0003466666667,0.0003733333333,0.0003866666667,0.0004,0.0003733333333,0.0003466666667,0.00032,0.00028,0.0002666666667,0.0002933333333,0.00032,0.0003733333333,0.0003466666667,0.0002933333333,0.00024,0.0002133333333;0.0001866666667,0.0002,0.0002266666667,0.0002533333333,0.0002666666667,0.0002933333333,0.0003066666667,0.00032,0.0003466666667,0.0003733333333,0.0003866666667,0.0004,0.0003733333333,0.0003466666667,0.00032,0.00028,0.0002666666667,0.0002933333333,0.00032,0.0003733333333,0.0003466666667,0.0002933333333,0.00024,0.0002133333333;0.0001866666667,0.0002,0.0002266666667,0.0002533333333,0.0002666666667,0.0002933333333,0.0003066666667,0.00032,0.0003466666667,0.0003733333333,0.0003866666667,0.0004,0.0003733333333,0.0003466666667,0.00032,0.00028,0.0002666666667,0.0002933333333,0.00032,0.0003733333333,0.0003466666667,0.0002933333333,0.00024,0.0002133333333;0.0002333333333,0.00025,0.0002833333333,0.0003166666667,0.0003333333333,0.0003666666667,0.0003833333333,0.0004,0.0004333333333,0.0004666666667,0.0004833333333,0.0005,0.0004666666667,0.0004333333333,0.0004,0.00035,0.0003333333333,0.0003666666667,0.0004,0.0004666666667,0.0004333333333,0.0003666666667,0.0003,0.0002666666667;0.0009333333333,0.001,0.001133333333,0.001266666667,0.001333333333,0.001466666667,0.001533333333,0.0016,0.001733333333,0.001866666667,0.001933333333,0.002,0.001866666667,0.001733333333,0.0016,0.0014,0.001333333333,0.001466666667,0.0016,0.001866666667,0.001733333333,0.001466666667,0.0012,0.001066666667;0.0009333333333,0.001,0.001133333333,0.001266666667,0.001333333333,0.001466666667,0.001533333333,0.0016,0.001733333333,0.001866666667,0.001933333333,0.002,0.001866666667,0.001733333333,0.0016,0.0014,0.001333333333,0.001466666667,0.0016,0.001866666667,0.001733333333,0.001466666667,0.0012,0.001066666667;0.0001166666667,0.000125,0.0001416666667,0.0001583333333,0.0001666666667,0.0001833333333,0.0001916666667,0.0002,0.0002166666667,0.0002333333333,0.0002416666667,0.00025,0.0002333333333,0.0002166666667,0.0002,0.000175,0.0001666666667,0.0001833333333,0.0002,0.0002333333333,0.0002166666667,0.0001833333333,0.00015,0.0001333333333;0.0001166666667,0.000125,0.0001416666667,0.0001583333333,0.0001666666667,0.0001833333333,0.0001916666667,0.0002,0.0002166666667,0.0002333333333,0.0002416666667,0.00025,0.0002333333333,0.0002166666667,0.0002,0.000175,0.0001666666667,0.0001833333333,0.0002,0.0002333333333,0.0002166666667,0.0001833333333,0.00015,0.0001333333333;9.333333333e-05,0.0001,0.0001133333333,0.0001266666667,0.0001333333333,0.0001466666667,0.0001533333333,0.00016,0.0001733333333,0.0001866666667,0.0001933333333,0.0002,0.0001866666667,0.0001733333333,0.00016,0.00014,0.0001333333333,0.0001466666667,0.00016,0.0001866666667,0.0001733333333,0.0001466666667,0.00012,0.0001066666667;0.0003266666667,0.00035,0.0003966666667,0.0004433333333,0.0004666666667,0.0005133333333,0.0005366666667,0.00056,0.0006066666667,0.0006533333333,0.0006766666667,0.0007,0.0006533333333,0.0006066666667,0.00056,0.00049,0.0004666666667,0.0005133333333,0.00056,0.0006533333333,0.0006066666667,0.0005133333333,0.00042,0.0003733333333;0.0028,0.003,0.0034,0.0038,0.004,0.0044,0.0046,0.0048,0.0052,0.0056,0.0058,0.006,0.0056,0.0052,0.0048,0.0042,0.004,0.0044,0.0048,0.0056,0.0052,0.0044,0.0036,0.0032;0.0003266666667,0.00035,0.0003966666667,0.0004433333333,0.0004666666667,0.0005133333333,0.0005366666667,0.00056,0.0006066666667,0.0006533333333,0.0006766666667,0.0007,0.0006533333333,0.0006066666667,0.00056,0.00049,0.0004666666667,0.0005133333333,0.00056,0.0006533333333,0.0006066666667,0.0005133333333,0.00042,0.0003733333333;0.0004666666667,0.0005,0.0005666666667,0.0006333333333,0.0006666666667,0.0007333333333,0.0007666666667,0.0008,0.0008666666667,0.0009333333333,0.0009666666667,0.001,0.0009333333333,0.0008666666667,0.0008,0.0007,0.0006666666667,0.0007333333333,0.0008,0.0009333333333,0.0008666666667,0.0007333333333,0.0006,0.0005333333333;0.0001866666667,0.0002,0.0002266666667,0.0002533333333,0.0002666666667,0.0002933333333,0.0003066666667,0.00032,0.0003466666667,0.0003733333333,0.0003866666667,0.0004,0.0003733333333,0.0003466666667,0.00032,0.00028,0.0002666666667,0.0002933333333,0.00032,0.0003733333333,0.0003466666667,0.0002933333333,0.00024,0.0002133333333;0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0];%节点无功(何立夫数据);
%线路参数
Line=[1,1,2;2,2,3;3,3,4;4,4,5;5,5,6;6,6,7;7,7,8;8,8,9;9,9,10;10,10,11;11,11,12;12,12,13;13,13,14;14,14,15;15,15,16;16,16,17;17,5,25;18,25,26;19,26,27;20,27,28;21,28,29;22,29,30;23,30,31;24,31,32;25,1,18;26,18,19;27,19,20;28,20,21;29,2,22;30,22,23;31,23,24;32,33,1];%支路数据;
Pd=0.000018;%放电功率;
Pc=0.000018;%充电功率;
Ndsum=[0;0;0;0;0;0;0;0;160;160;160;160;160;160;0;0;0;0;0;160;80;0;0;0];%上层调度放电电动汽车数量(何立夫数据);
Ncsum=[380;380;380;360;110;0;0;0;0;0;0;0;0;0;0;0;60;0;0;0;0;0;350;380];%上层调度充电电动汽车数量(何立夫数据);
Nd_resid=zeros(24,1);Nc_resid=zeros(24,1);Nd_comme=zeros(24,1);Nc_comme=zeros(24,1);Nd_indus=zeros(24,1);Nc_indus=zeros(24,1);%区域电动汽车数量;
for t=1:24%不同时间段不同区域电动汽车充、放电数量,下述只是计算数量,也可直接采用数据来表示,不用纠结公式如何来
if t<=17
Nd_resid(t)=0.7*6/112*Ndsum(t);Nd_comme(t)=(0.2+0.7*16/112)*Ndsum(t);Nd_indus(t)=(0.1+0.7*90/112)*Ndsum(t);%何立夫数据;
else
Nd_resid(t)=0.7*Ndsum(t);Nd_comme(t)=0.2*Ndsum(t);Nd_indus(t)=0.1*Ndsum(t);
end
if t>=8&t<=19
Nc_resid(t)=0.7/21*Ncsum(t);Nc_comme(t)=(0.2+0.7*6/42)*Ncsum(t);Nc_indus(t)=(0.1+0.7*34/42)*Ncsum(t);%何立夫数据;
else
Nc_resid(t)=0.7*Ncsum(t);Nc_comme(t)=0.2*Ncsum(t);Nc_indus(t)=0.1*Ncsum(t);
end
end
%节点导纳、电纳参数
G=[21.4943686300000,-2.58137264300000,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-5.11502111900000,0,0];%节点导纳矩阵实部;
B=[-13.2295494500000,1.31477215100000,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,4.88110247000000,0,0,];%节点导纳矩阵虚部;
%节点电压最小、最大值
Vmin=[0.93;0.93;0.93;0.93;0.93;0.93;0.93;0.93;0.93;0.93;0.93;0.93;0.93;0.93;0.93;0.93;0.93;0.93;0.93;0.93;0.93;0.93;0.93;0.93;0.93;0.93;0.93;0.93;0.93;0.93;0.93;0.93];%节点电压最小值;
Vmax=[1.07;1.07;1.07;1.07;1.07;1.07;1.07;1.07;1.07;1.07;1.07;1.07;1.07;1.07;1.07;1.07;1.07;1.07;1.07;1.07;1.07;1.07;1.07;1.07;1.07;1.07;1.07;1.07;1.07;1.07;1.07;1.07];%节点电压最大值;
Plinemax=0.11;%线路功率传输上限;
%%%%%%%%%分时段%%%%%%%%%%
Ploss=zeros(24,1);Nd_data=zeros(33,24);Nc_data=zeros(33,24);Volta=zeros(33,24);Theta=zeros(33,24);
parfor t=1:24
%%%%%%%%%MISOCP模型求解%%%%%%%%%%
u=sdpvar(32,1);%u=Volta^2;电压平方变量
R=sdpvar(32,1);%R=Volta(i)*Volta(j)*cos(Theta(i)-Theta(j));
T=sdpvar(32,1);%T=Volta(i)*Volta(j)*sin(Theta(i)-Theta(j));
Nd=intvar(32,1);%放电电动汽车数量
Nc=intvar(32,1);%充电电动汽车数量
%%%%%%%%%%%目标函数%%%%%%%%%;
f=0;%网损
for i=1:16
f=f-G(i,i+1)*(u(i)+u(i+1)-2*R(i));
end
f=f-G(5,25)*(u(5)+u(25)-2*R(17));
for i=18:24
f=f-G(i+7,i+8)*(u(i+7)+u(i+8)-2*R(i));
end
f=f-G(1,18)*(u(1)+u(18)-2*R(25));
for i=26:28
f=f-G(i-8,i-7)*(u(i-8)+u(i-7)-2*R(i));
end
f=f-G(2,22)*(u(2)+u(22)-2*R(29));
for i=30:31
f=f-G(i-8,i-7)*(u(i-8)+u(i-7)-2*R(i));
end
f=f-G(33,1)*(1.05*1.05+u(1)-2*R(32));
%%%%%约束条件%%%%%%%%
C=[R>=0,u>=Vmin.^2,u<=Vmax.^2,Nd>=0,Nc>=0,Nc<=50,Nd<=50];%电压、充放电电动汽车约束
%%%%%潮流方程%%%%%%%%根据33节点网络进行一一的潮流公式书写,如1节点和2节点相连,就把相连节点的部分作为潮流约束的一部分,不相连的部分不考虑,但是这种方法编程挺麻烦
C=[C,Pload(1,t)+Nc(1)*Pc-Nd(1)*Pd==G(1,33)*u(1)-G(1,33)*R(32)+B(1,33)*T(32)+G(1,2)*u(1)-G(1,2)*R(1)-B(1,2)*T(1)+G(1,18)*u(1)-G(1,18)*R(25)-B(1,18)*T(25)];
C=[C,Qload(1,t)==-B(1,33)*u(1)+B(1,33)*R(32)+G(1,33)*T(32)-B(1,2)*u(1)+B(1,2)*R(1)-G(1,2)*T(1)-B(1,18)*u(1)+B(1,18)*R(25)-G(1,18)*T(25)];
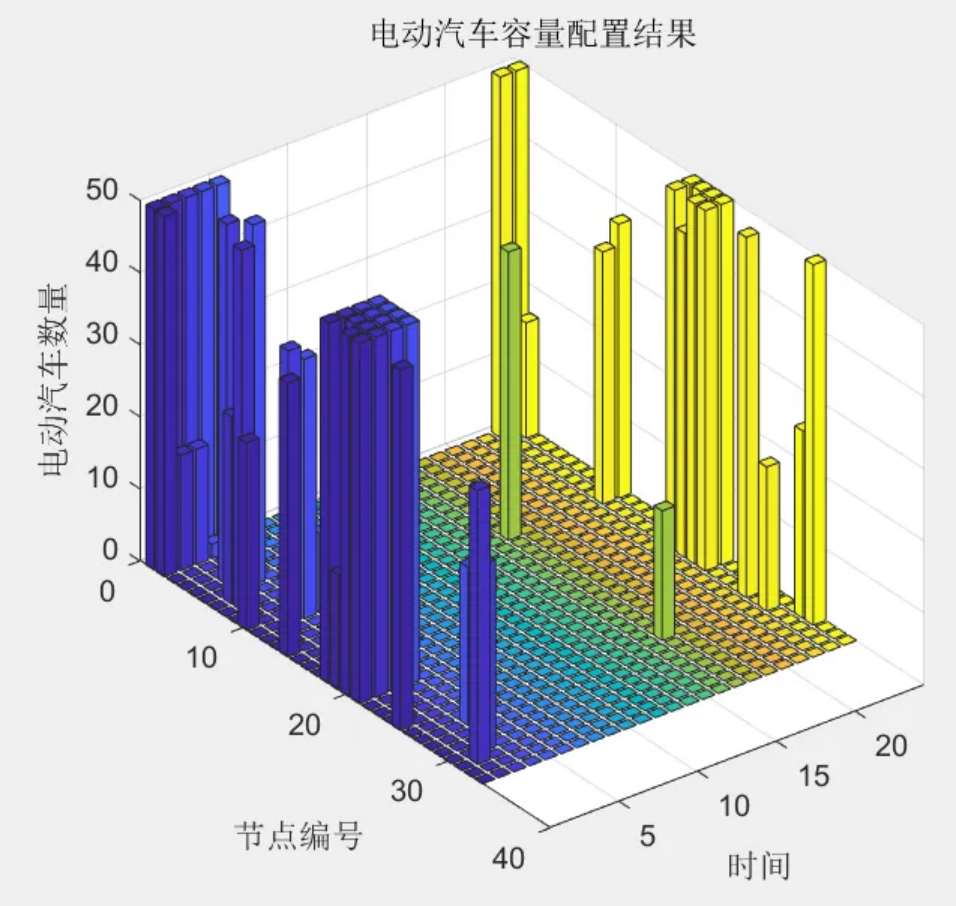
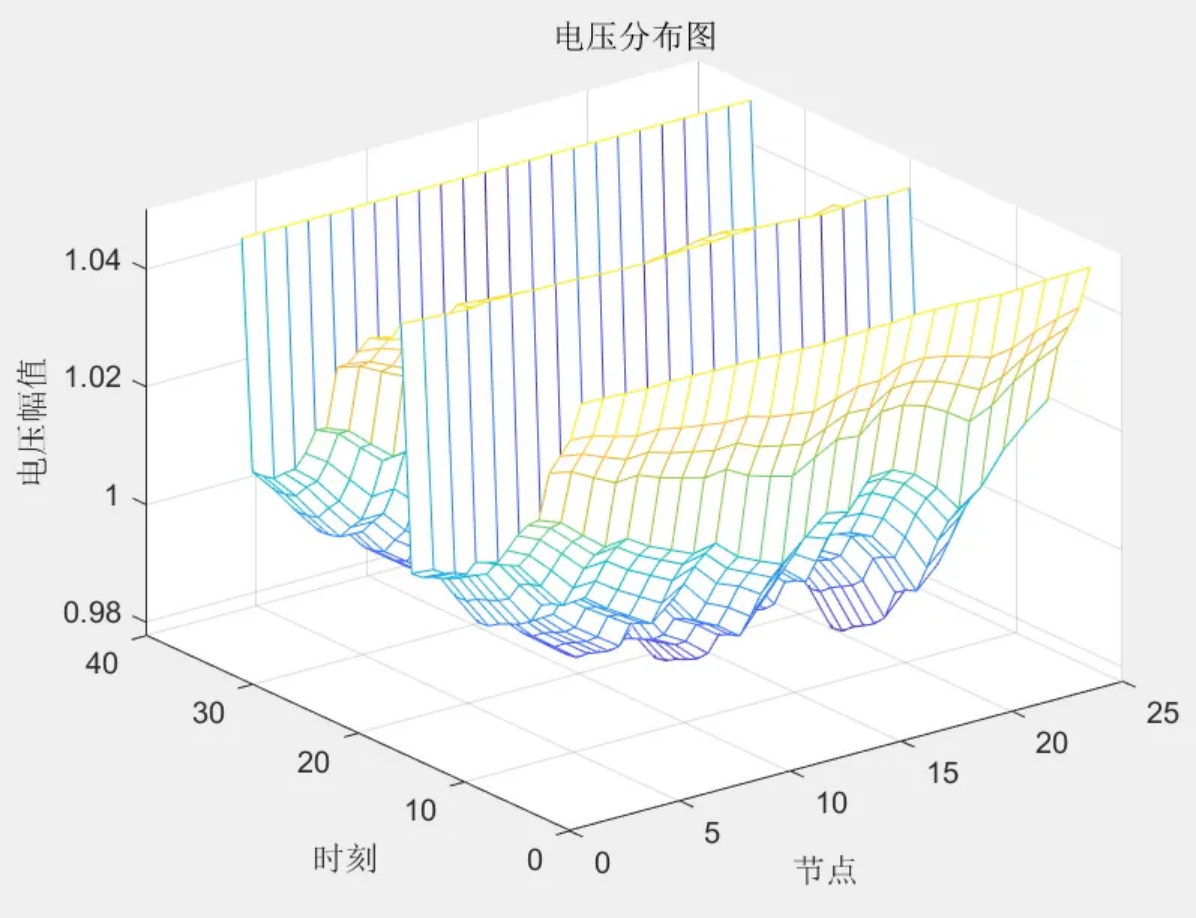
3 程序结果