从MLP到卷积 - 技术栈

1.从MLP到卷积层

最近要做多通道的实验，所以重新将处理图像的基础模型回顾一下，什么是卷积？卷积本质是是一种特殊的全连接层。

1.1怎么w的权重从一个值变成了4维呢?可以这样理解，在此举一个例子：

其实本质可以看成，将w的权重从一个值拉成了一个向量，ij就是宽与高，对应的向量就是具体的元素值，我们在这里假设w形状为2*2*3*3.这个怎么理解四维张量呢？2是两个批次，

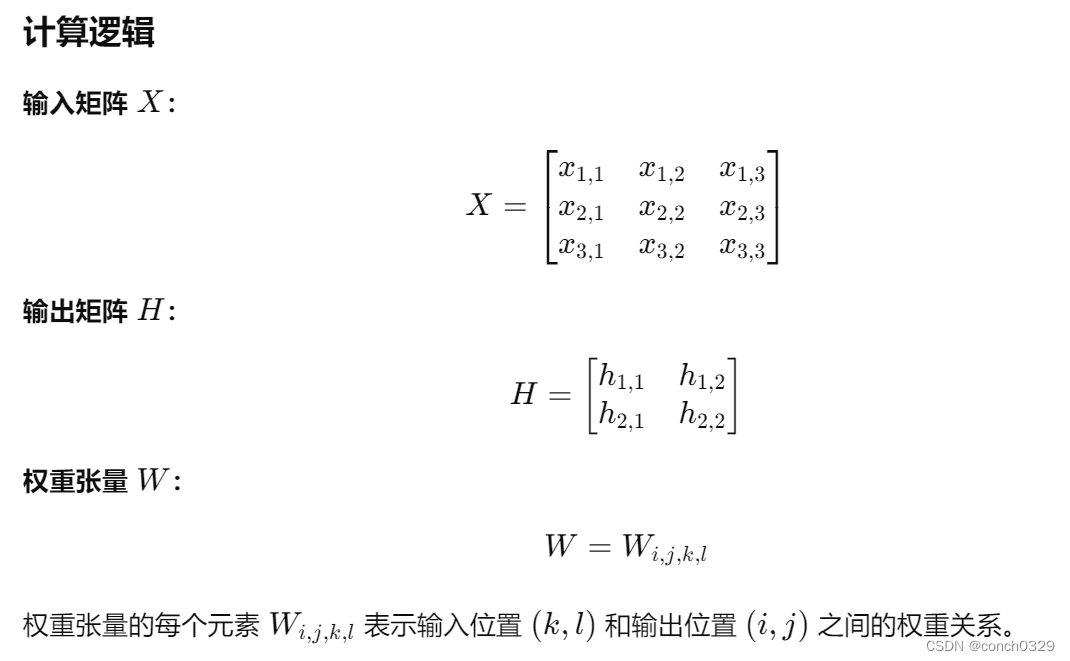
对于输入矩阵和输出矩阵的维度，以及四维张量权重的形状，可以用一个具体的示例来说明它们之间的关系。

示例设定

输入矩阵 𝑋X 大小为 3×3。
输出矩阵 𝐻H 大小为 2×2。
权重张量 𝑊W 形状为 2×2×3×3

python 复制代码

#第一个输出神经元
      x11  ---- W1111 ----
      x12  ---- W1112 ----
      x13  ---- W1113 ----
      x21  ---- W1121 ----> h11
      x22  ---- W1122 ----
      x23  ---- W1123 ----
      x31  ---- W1131 ----
      x32  ---- W1132 ----
      x33  ---- W1133 ----
#第二个输出神经元
      x11  ---- W1211 ----
      x12  ---- W1212 ----
      x13  ---- W1213 ----
      x21  ---- W1221 ----> h12
      x22  ---- W1222 ----
      x23  ---- W1223 ----
      x31  ---- W1231 ----
      x32  ---- W1232 ----
      x33  ---- W1233 ----
#第三个输出神经元
      x11  ---- W2111 ----
      x12  ---- W2112 ----
      x13  ---- W2113 ----
      x21  ---- W2121 ----> h21
      x22  ---- W2122 ----
      x23  ---- W2123 ----
      x31  ---- W2131 ----
      x32  ---- W2132 ----
      x33  ---- W2133 ----
#第四个输出神经元
      x11  ---- W2211 ----
      x12  ---- W2212 ----
      x13  ---- W2213 ----
      x21  ---- W2221 ----> h22
      x22  ---- W2222 ----
      x23  ---- W2223 ----
      x31  ---- W2231 ----
      x32  ---- W2232 ----
      x33  ---- W2233 ----

这个对应的是输出。也就是2*2的一个输出。2*2*3*3前者是输出的维度，后者是输入的维度。其实权重就是把w原先的1维变成了矩阵，每个都对应相乘了。这个是mlp和卷积的关系。卷积是一种特殊的mlp。所以一般的卷积是什么呢？

一般的卷积满足下面两个性质：

（1）平移不变性

（2）局部性

给一个图和一个卷积核的定义就能理解了：在这里卷积核就是3*3了，平移确实没有变化卷积核，卷积核就是权重矩阵，局部性就是每个卷积核就那么大，滚来滚去还是那么大。

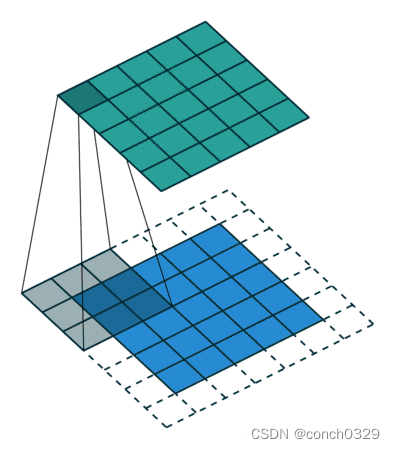
1.2怎么理解卷积呢？

1.3多个输入与输出通道

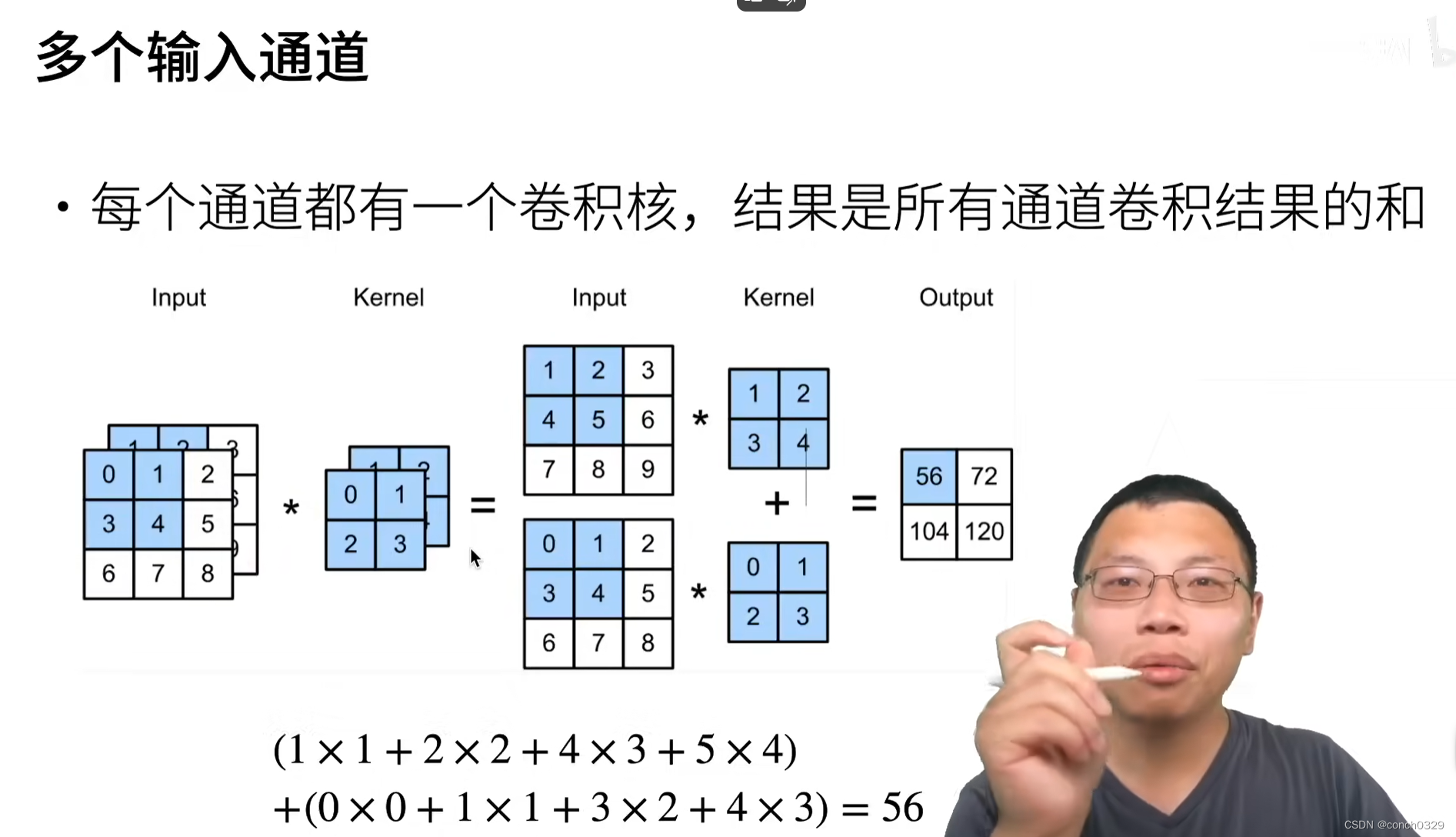
一个自己写的例子：

多对一

python 复制代码

import torch
from d2l import torch as d2l
import numpy as np
def corr2d_multi_in(X,K):
    return sum(d2l.corr2d(x,k) for x,k in zip(X,K))
X = torch.tensor([[[0,1,2],[3,4,5],[6,7,8]],
                 [[1,2,3],[4,5,6],[7,8,9]],
                  [[2,3,4],[5,6,7],[8,9,10]]])

K = torch.tensor([[[0,1],[2,3]],[[1,2],[3,4]],[[5,6],[7,8]]])
print(corr2d_multi_in(X,K))

这个怎么理解呢？就是三个卷积核对应着三个不同的通道。

结果如下最后要将三个卷积核计算的结果进行相加。sum三个卷积核。

多对多（多通道输入及多通道输出）：

老样子，我还是举个例子：

（1）定义输入和卷积核

python 复制代码

import torch

# 定义输入张量 X
X = torch.tensor([[[0, 1, 2], 
                   [3, 4, 5], 
                   [6, 7, 8]], 

                  [[1, 2, 3], 
                   [4, 5, 6], 
                   [7, 8, 9]]])

# 定义原始卷积核 K
K = torch.tensor([[[0, 1], 
                   [2, 3]], 

                  [[1, 2], 
                   [3, 4]]])

# 扩展 K
K = torch.stack((K, K + 1, K + 2), 0)

（2）扩展后的卷积核

python 复制代码

K = torch.stack((K, K+1, K+2), 0)

# 结果
K = tensor([[[[0, 1], [2, 3]],  # 第一个卷积核
             [[1, 2], [3, 4]]], 

            [[[1, 2], [3, 4]],  # 第二个卷积核 (K+1)
             [[2, 3], [4, 5]]], 

            [[[2, 3], [4, 5]],  # 第三个卷积核 (K+2)
             [[3, 4], [5, 6]]]])

（3）定义二维卷积函数

python 复制代码

def corr2d(X, K):
    h, w = K.shape
    Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i, j] = (X[i: i + h, j: j + w] * K).sum()#这一块是卷积核，对应的就是移动小方框的累计求和
    return Y

（4）多通道输入二维卷积函数

python 复制代码

def corr2d_multi_in(X, K):
    return sum(corr2d(x, k) for x, k in zip(X, K))

（5）最终多输入多输出的卷积函数

python 复制代码

def corr2d_multi_in_out(X, K):
    return torch.stack([corr2d_multi_in(X, k) for k in K], 0)

（6）调用并打印结果

python 复制代码

result = corr2d_multi_in_out(X, K)
print(result)

给出结果：

（1）第一个卷积核 k = K[0]:

python 复制代码

k = tensor([[[0, 1], 
             [2, 3]], 

            [[1, 2], 
             [3, 4]]])

（2）对第一个通道:

python 复制代码

x = X[0] = tensor([[0, 1, 2], 
                   [3, 4, 5], 
                   [6, 7, 8]])
k[0] = tensor([[0, 1], 
               [2, 3]])

result = corr2d(x, k[0])
# result: tensor([[19, 25], [37, 43]])

（3）对第二个通道:

python 复制代码

x = X[1] = tensor([[1, 2, 3], 
                   [4, 5, 6], 
                   [7, 8, 9]])
k[1] = tensor([[1, 2], 
               [3, 4]])

result = corr2d(x, k[1])
# result: tensor([[42, 52], [72, 82]])

（4）两个通道结果相加:

python 复制代码

total_result = tensor([[19, 25], [37, 43]]) + tensor([[42, 52], [72, 82]])
# total_result: tensor([[ 61,  77], [109, 125]])

（5）第二个卷积核 k = K[1]:

python 复制代码

k = tensor([[[1, 2], 
             [3, 4]], 

            [[2, 3], 
             [4, 5]]])

（6）对第一个通道:

python 复制代码

x = X[0] = tensor([[0, 1, 2], 
                   [3, 4, 5], 
                   [6, 7, 8]])
k[0] = tensor([[1, 2], 
               [3, 4]])

result = corr2d(x, k[0])
# result: tensor([[39, 49], [69, 79]])

（7）对于第二个通道

python 复制代码

x = X[1] = tensor([[1, 2, 3], 
                   [4, 5, 6], 
                   [7, 8, 9]])
k[1] = tensor([[2, 3], 
               [4, 5]])

result = corr2d(x, k[1])
# result: tensor([[64, 79], [109, 124]])

（8）两个通道结果相加:

python 复制代码

total_result = tensor([[39, 49], [69, 79]]) + tensor([[64, 79], [109, 124]])
# total_result: tensor([[103, 128], [178, 203]])

（9）第三个卷积核 k = K[2]:

python 复制代码

k = tensor([[[2, 3], 
             [4, 5]], 

            [[3, 4], 
             [5, 6]]])

（10）对第一个通道:

python 复制代码

x = X[0] = tensor([[0, 1, 2], 
                   [3, 4, 5], 
                   [6, 7, 8]])
k[0] = tensor([[2, 3], 
               [4, 5]])

result = corr2d(x, k[0])
# result: tensor([[59, 73], [101, 115]])

（11）对第二个通道:

python 复制代码

x = X[1] = tensor([[1, 2, 3], 
                   [4, 5, 6], 
                   [7, 8, 9]])
k[1] = tensor([[3, 4], 
               [5, 6]])

result = corr2d(x, k[1])
# result: tensor([[86, 106], [146, 166]])

（12）两个通道结果相加:

python 复制代码

total_result = tensor([[59, 73], [101, 115]]) + tensor([[86, 106], [146, 166]])
# total_result: tensor([[145, 179], [247, 281]])

（13）堆叠所有结果

python 复制代码

final_result = torch.stack([tensor([[ 61,  77], [109, 125]]),
                            tensor([[103, 128], [178, 203]]),
                            tensor([[145, 179], [247, 281]])], 0)

# final_result:
# tensor([[[ 61,  77],
#          [109, 125]],

#         [[103, 128],
#          [178, 203]],

#         [[145, 179],
#          [247, 281]]])