卡尔曼滤波（Kalman Filtering）详细解读

🔥当前正在更新专栏： 《VUE》、《JavaScript保姆级教程》、《krpano》、《krpano中文文档》

✨ 前言

卡尔曼滤波（Kalman Filtering）是一种用于估计动态系统状态的递推算法，被广泛应用于控制系统、信号处理、经济学、导航和机器人学等领域。它是由瑞典数学家鲁道夫·卡尔曼（Rudolf E. Kalman）于1960年提出的，因其在多种应用中的卓越表现，被誉为20世纪最重要的发明之一。本文将从卡尔曼滤波的基本原理、数学推导、应用实例以及代码实现等方面进行详细解读，帮助读者深入理解这一强大的工具。

✨ 正文

一、卡尔曼滤波的基本原理

卡尔曼滤波是一种线性二次估计器，旨在通过对一系列带有噪声的观测数据进行处理，估计出系统的真实状态。其核心思想是基于贝叶斯理论，通过递归估计来不断更新系统的状态和协方差矩阵，从而获得最优估计。

1.1 系统模型

卡尔曼滤波假设系统可以用线性状态空间模型表示，即：

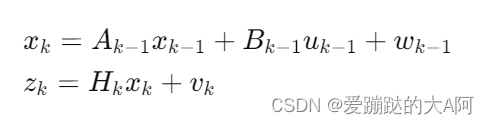
其中：

xkx_{k}xk 是时刻 kkk 的状态向量；
Ak−1A_{k-1}Ak−1 是状态转移矩阵；
Bk−1B_{k-1}Bk−1 是控制输入矩阵；
uk−1u_{k-1}uk−1 是控制向量；
wk−1w_{k-1}wk−1 是过程噪声，假设为零均值高斯噪声，协方差为 Qk−1Q_{k-1}Qk−1；
zkz_{k}zk 是时刻 kkk 的观测向量；
HkH_{k}Hk 是观测矩阵；
vkv_{k}vk 是观测噪声，假设为零均值高斯噪声，协方差为 RkR_{k}Rk。

1.2 卡尔曼滤波的两大步骤

卡尔曼滤波主要分为预测（Predict）和更新（Update）两个步骤：

预测步骤 ：在时刻 k−1k-1k−1 已知状态估计 x^k−1∣k−1\hat{x}{k-1|k-1}x^k−1∣k−1 和协方差矩阵 Pk−1∣k−1P{k-1|k-1}Pk−1∣k−1 的情况下，预测时刻 kkk 的状态和协方差矩阵：
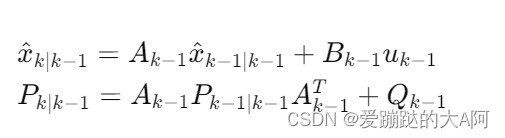
更新步骤 ：在得到时刻 kkk 的观测值 zkz_{k}zk 后，更新状态估计和协方差矩阵：

二、卡尔曼滤波的数学推导

为了更深入理解卡尔曼滤波，我们需要从概率的角度推导其更新公式。

2.1 预测步骤推导

预测步骤基于系统的状态转移模型，计算在没有观测信息时对下一个时刻状态的估计。

根据系统状态方程：

2.2 更新步骤推导

更新步骤结合观测信息，利用贝叶斯定理修正预测结果。

观测方程为：

三、卡尔曼滤波的应用实例

为了更好地理解卡尔曼滤波的应用，我们将介绍两个经典的实例：位置跟踪和金融数据预测。

3.1 位置跟踪

在位置跟踪应用中，卡尔曼滤波可以用来估计物体的当前位置和速度。

假设物体的运动模型为：

3.2 金融数据预测

在金融数据预测中，卡尔曼滤波可以用来估计和预测股票价格。

假设股票价格的变动遵循随机游走模型：

使用卡尔曼滤波可以递推估计当前的股票价格，并根据历史数据进行预测。

四、卡尔曼滤波的代码实现

下面我们将展示卡尔曼滤波的Python实现，以位置跟踪为例。

python 复制代码

import numpy as np

class KalmanFilter:
    def __init__(self, A, B, H, Q, R, P, x0):
        self.A = A  # 状态转移矩阵
        self.B = B  # 控制输入矩阵
        self.H = H  # 观测矩阵
        self.Q = Q  # 过程噪声协方差矩阵
        self.R = R  # 观测噪声协方差矩阵
        self.P = P  # 估计误差协方差矩阵
        self.x = x0 # 初始状态估计

    def predict(self, u):
        # 状态预测
        self.x = np.dot(self.A, self.x) + np.dot(self.B, u)
        # 误差协方差预测
        self.P = np.dot(np.dot(self.A, self.P), self.A.T) + self.Q

    def update(self, z):
        # 卡尔曼增益
        S = np.dot(np.dot(self.H, self.P), self.H.T) + self.R
        K = np.dot(np.dot(self.P, self.H.T), np.linalg.inv(S))
        # 更新状态估计
        self.x = self.x + np.dot(K, (z - np.dot(self.H, self.x)))
        # 更新误差协方差
        I = np.eye(self.P.shape[0])
        self.P = np.dot(np.dot(I - np.dot(K, self.H), self.P), 
                        (I - np.dot(K, self.H)).T) + np.dot(np.dot(K, self.R), K.T)

# 示例参数设置
dt = 1.0  # 时间间隔
A = np.array([[1, dt], [0, 1]])  # 状态转移矩阵
B = np.array([[0.5*dt**2], [dt]])  # 控制输入矩阵
H = np.array([[1, 0]])  # 观测矩阵
Q = np.array([[0.1, 0], [0, 0.1]])  # 过程噪声协方差
R = np.array([[1]])  # 观测噪声协方差
P = np.eye(2)  # 初始误差协方差
x0 = np.array([0, 1])  # 初始状态

kf = KalmanFilter(A, B, H, Q, R, P, x0)

# 模拟控制输入和观测
u = np.array([0])  # 假设没有控制输入
measurements = [np.array([1]), np.array([2]), np.array([3])]  # 观测数据

for z in measurements:
    kf.predict(u)  # 预测步骤
    kf.update(z)   # 更新步骤
    print(f"状态估计: {kf.x}")

五、卡尔曼滤波的扩展

卡尔曼滤波虽然强大，但也有局限性。例如，它假设系统是线性且噪声服从高斯分布。对于非线性系统，可以使用扩展卡尔曼滤波（EKF）或无迹卡尔曼滤波（UKF）。这些滤波器在处理非线性问题时表现更优。

5.1 扩展卡尔曼滤波

扩展卡尔曼滤波通过对非线性系统进行线性化处理，适用于处理小非线性的系统。其主要步骤如下：

预测步骤 ：使用非线性状态转移方程进行状态预测：
更新步骤 ：使用非线性观测方程进行状态更新：

5.2 无迹卡尔曼滤波

无迹卡尔曼滤波采用无迹变换来处理非线性系统，其不需要对系统进行线性化，适用于强非线性系统。

无迹卡尔曼滤波的主要步骤包括：

生成一组无迹采样点；
通过非线性函数传播这些采样点；
根据传播后的采样点计算状态估计和协方差矩阵。

无迹卡尔曼滤波的具体实现较为复杂，这里不做详细展开。

✨ 结语

卡尔曼滤波是一种强大的估计工具，广泛应用于各个领域。通过递推估计和贝叶斯理论，卡尔曼滤波能够在有噪声的观测数据中有效地估计系统的真实状态。虽然它有一定的局限性，但扩展卡尔曼滤波和无迹卡尔曼滤波等变种进一步扩展了其应用范围。通过实际应用和代码实现，可以更好地理解卡尔曼滤波的工作原理和效果。

希望本文能够帮助读者深入理解卡尔曼滤波，并在实际工作中灵活应用这一工具。