6.1懒惰是一种美德
如果你 在一个地方编写了一些代码，但需要在另一个地方再次使用，该如何办呢？
假设你编写了一段代码，它计算一些斐波那契数（一种数列，其中每个数都是前两个数的和）。
现在的数列包含10个斐波那契数。
如果要使用这些数字做其他事情，该如何办呢？我们肯定不愿意再重新写一遍代码。我们可以让程序更抽象。要让前面的程序更抽象，可以像下面这样做：
大家可以看见，我在确定num后直接可以打印出fibs。其实如果把整体封装起来，就可以直接调用。
6.2抽象和结构
抽象可节省人力，但实际上还有个更重要的优点：抽象是程序能够被人理解的关键所在。
人和计算机的差别在于，计算机本身喜欢具体而明确的指 令，但人通常不是这样的。
例如：如果你向人打听怎么去电影院，就不希望对方回答："向前走10步，向左转90度，接着走5步，再向右转45度，然后走123步。"（这是计算机希望听见的）。"沿这条街往前走，看到过街天桥后走到马路对面，电影院就在你左边。"（这是人希望听见的）。这里的关键是你知道如何沿街往前走，也知道如何过天桥，因此不需要有关这些方面的具体说明。
组织计算机程序时，你也采取类似的方式。程序应非常抽象，如下载网页、计算使用频率、打印每个单词的使用频率。
看到这些代码，任何人都知道这个程序是做什么的。但是其中到底如何做，其中的细节会在其他地方给出。
6.3自定义函数
函数执行特定的操作并返回一个值，你可以调用它（调用时可能需要提供一些参数------放在圆括号中的内容）。一般而言，要判断某个对象是否可调用，可使用内置函数callable。
此时说明x是不可以调用的，y是可以的。（并非所有的函数都返回值）
函数是结构化编程的核心。那么如何定义函数呢？使用def（表示定义函数）语句。
上面两行是对于函数的简单定义，最下面是对函数的调用。
那现在回到斐波那契数，如果编写一个函数，返回一个由斐波那契数组成的列表呢？
前5行都是对于斐波那契数整个函数的定义，最后一行是对其进行调用。
其实我们不难发现，除了def一直需要外，我们在每个定义def中都有一个return语句。return语 句用于从函数返回值（在前面的hello函数中，return语句的作用也是一样的）。
6.3.1给函数编写文档
要给函数编写文档，以确保其他人能够理解，可添加注释（以#打头的内容）。
放在函数开头的字符串称为文档字符串（docstring），将作为函数的一部分存储起来。
代码前三行是定义，其中包含了我们的注释。最后一行我们先是调用了下函数进行计算，同时也读取了函数定义的文档字符串。（注意 __doc__是函数的一个属性。）
特殊的内置函数help很有用。在交互式解释器中，可使用它获取有关函数的信息，其中包含函数的文档字符串。
6.3.2其实并不是函数的函数
数学意义上的函数总是返回根据参数计算得到的结果。在Python中，有些函数什么都不返回。
什么都不返回的函数不包含return语句，或者包含return语句，但没有在return后面指定值。
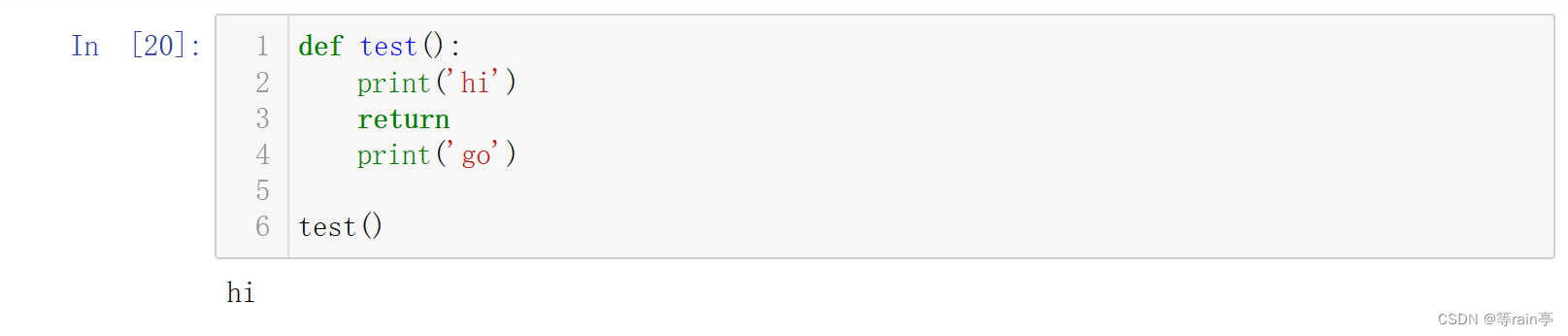这里虽然包含了return，但是其实return部分没有返回任何值，只是为了结束语句（第二个打印的go没有打印出来）（这有点像在循环中使用break，但跳出的是函数）
6.4参数魔法
函数使用起来很简单，创建起来也不那么复杂，但要习惯参数的工作原理就不那么容易了。
6.4.1值从哪里来
定义函数时，你可能心存疑虑：参数的值是怎么来的呢？
编写函数旨在为当前程序（甚至其他程序）提供服务，你的职责是确保它在提供的参数正确时完成任务，并在参数不对时以显而易见的方式失败。参数通常不需要担心。
在def语句中，位于函数名后面的变量通常称为形参，而调用函数时提供的值称为实参。很多情况下我们会将实参称为值，以便将其与类似于变量的形参区分开来。
6.4.2我能修改参数吗
参数不过是变量而已，行为与你预期的完全相同。在函数内部给参数赋值对外部没有任何影响。
在try_to_change内，将新值赋给了参数n，但如你所见，这对变量name没有影响。说到底，这是一个完全不同的变量。
这样可能更加直观，在有返回值的情况下，在定义里面修改参数会导致返回值的变化，但是但是重要的是它不会去修改我们的name。变量n变了，但变量name没变。同样，在函数内部重新关联参数（即给它赋值）时，函数外部的变量不受影响（参数存储在局部作用域内）。
字符串（以及数和元组）是不可变的（immutable），这意味着你不能修改它们（即只能替换为新值）。因此这些类型作为参数没什么可说的。但如果参数为可变的数据结构（如列表）呢？
唉？例子也是在函数内修改了参数，为什么函数外部的names发生变化了？大家先看下面：
这样的情况大家应该都见过，将同一个列表赋给两个变量时，这两个变量将同时指向这个列表。就这么简单。
这就解释了为什么在函数外的结果被修改了。
要避免这样的结果，必须创建列表的副本。对序列执行切片操作时，返回的切片都是副本。因此，如果你创建覆盖整个列表的切片，得到的将是列表的副本。
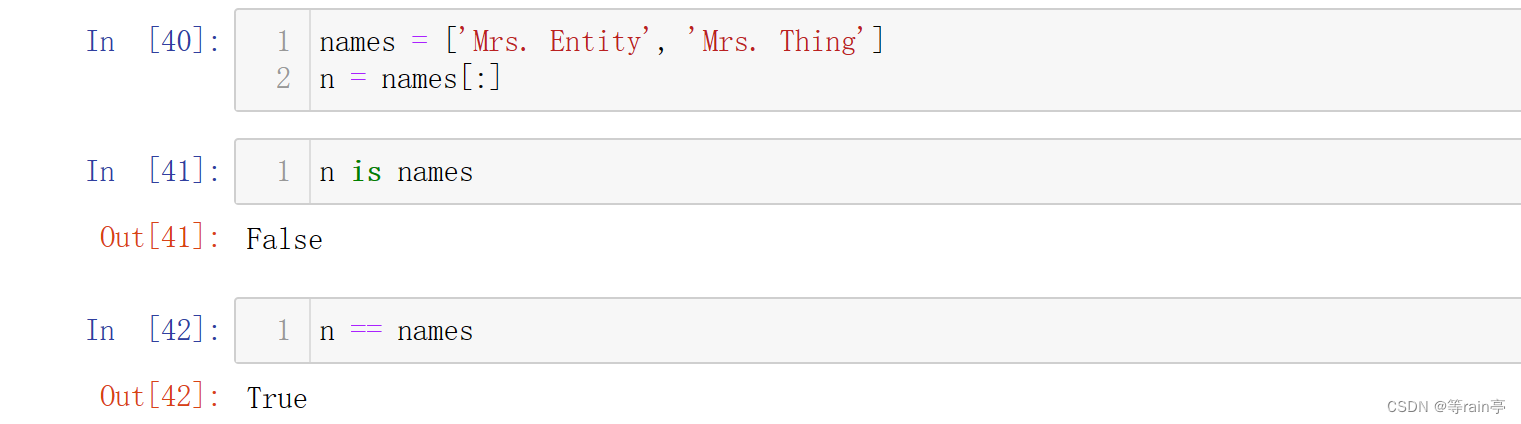
此时就可以发现，n和names虽然内容相同，但是已经不是同一个列表了。 注意到参数n包含的是副本。
（1）为何要修改参数
在提高程序的抽象程度方面，使用函数来修改数据结构（如列表或字典）是一种不错的方式。
假设你要编写一个程序，让它存储姓名，并让用户能够根据名字、中间名或 姓找人。为此，你可能使用一个类似于下面的数据结构：
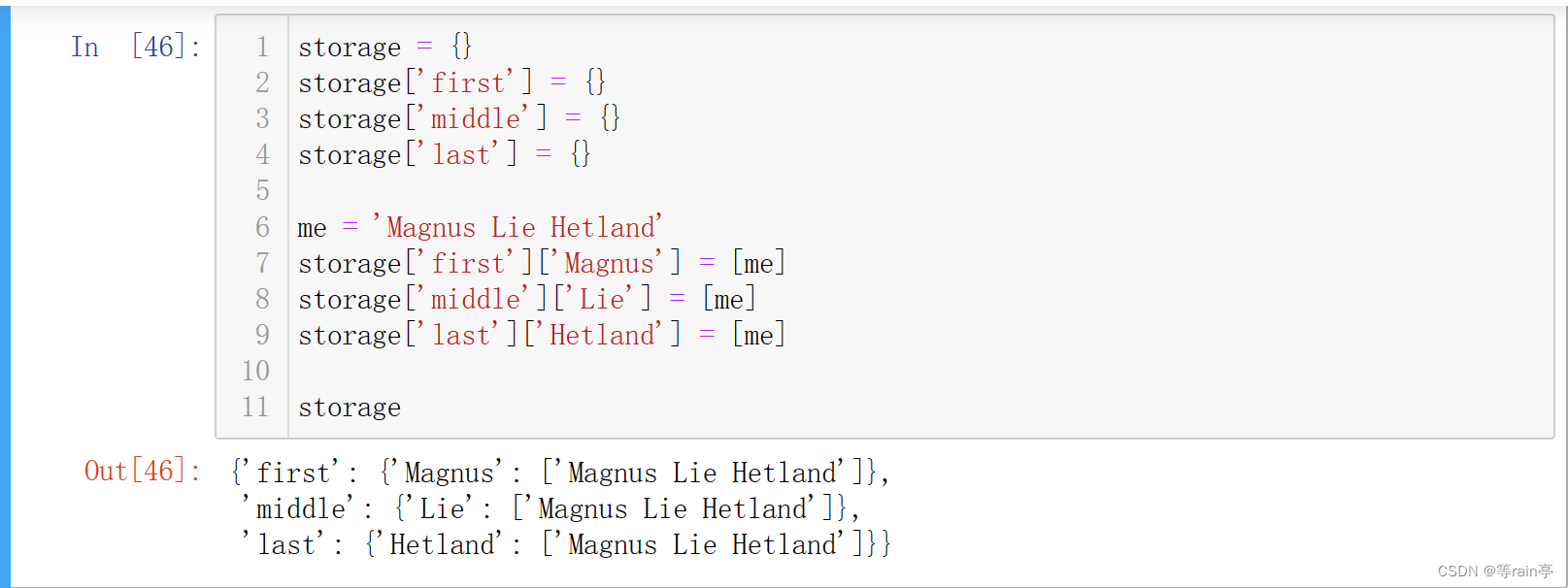
每个键下都存储了一个人员列表。在这个例子里，这些列表只包含作者。
现在，要获取中间名为Lie的人员名单，可像下面这样做：
但是，如你所见，将人员添加到这个数据结构中有点繁琐，在多个人的名字、中间名或姓相同时尤其如此，因为在这种情况下需要对存储在名字、中间名或姓下的列表进行扩展。
下面来添加我的妹妹，并假设我们不知道数据库中存储了什么内容。
storage['first']['Anne'] 在第一个代码的第二行给first键对应的'Anne'键对应的值用my_sister添加，由于之前我们并没有对Anne的键对应相应的值，现在直接添加，形成的结果就是刚刚添加的。对于三行的Lie之前我们有设置过值，现在append一个，最后得到的结果就是第二个代码出现的结果。
可以想见，编写充斥着这种更新的大型程序时，代码将很快变得混乱不堪。
抽象的关键在于隐藏所有的更新细节，为此可使用函数。下面首先来创建一个初始化数据结构的函数。
你所见，这个函数承担了初始化职责，让代码的可读性高了很多。
接下来设计获取人员姓名的函数。
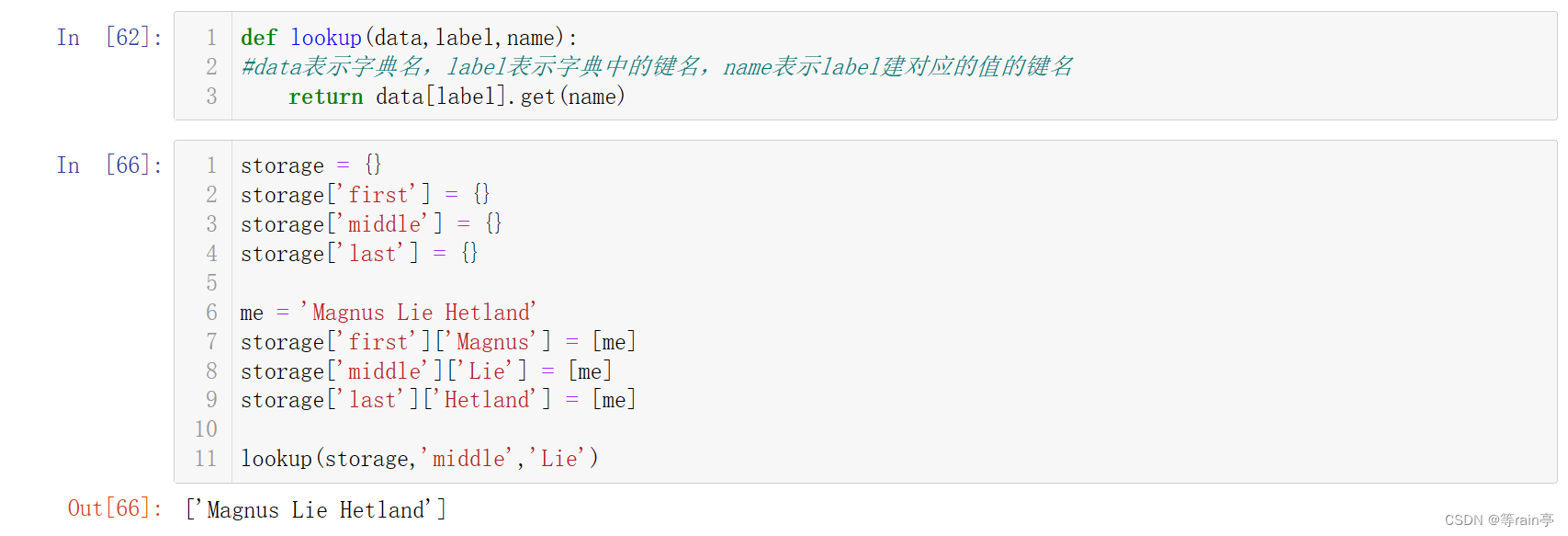
第一个代码就是获取设计人员姓名的函数。第二个代码最后就是对该函数的使用。
下面来编写将人员存储到数据结构中的函数。
运行一下：
如你所见，如果多个人的名字、中间名或姓相同，可同时获取这些人员。
(2)如果参数是不可变的
在很多语言中，经常需要给参数赋值并让这种修改影响函数外部的变量。在Python中，没法直接这样做，只能修改参数对象本身。
但是，如果参数不可变呢？没办法。在这种情况下，应从函数返回所有需要的值（如果需要返回多个值，就以元组的方式返回它们）。
这样没有进过修改参数
如果一定要修改参数，改变外部的值，可以把值放在列表中。
6.4.3关键字参数和默认值
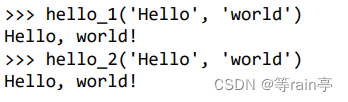
有时候，参数的排列顺序可能难以记住，尤其是参数很多时。
但是当我们改成这样的时候参数的顺序就无关紧要了，但是名称变的很重要。
像这样使用名称指定的参数称为关键字参数，主要优点是有助于澄清各个参数的作用。
虽然这样做的输入量多些，但每个参数的作用清晰明了。另外，参数的顺序错了也没关系。
然而，关键字参数最大的优点在于，可以指定默认值。
像这样，设定完默认值后，调用时不提供它，也可以运行出来。
当然也可以提供默认值。提供1个或者2个都可以。
如你所见，这两个提供的值，其实还是按照位置进行分配的。那如何使用提供的name或者greeting。
还不止这些。你可结合使用位置参数和关键字参数，但必须先指定所有的位置参数，否则解释器将不知道它们是哪个参数（即不知道参数对应的位置）。通常不会结合位置参数和关键字参数。
大家可以自己看一下代码，思考一下与预期是否相同。
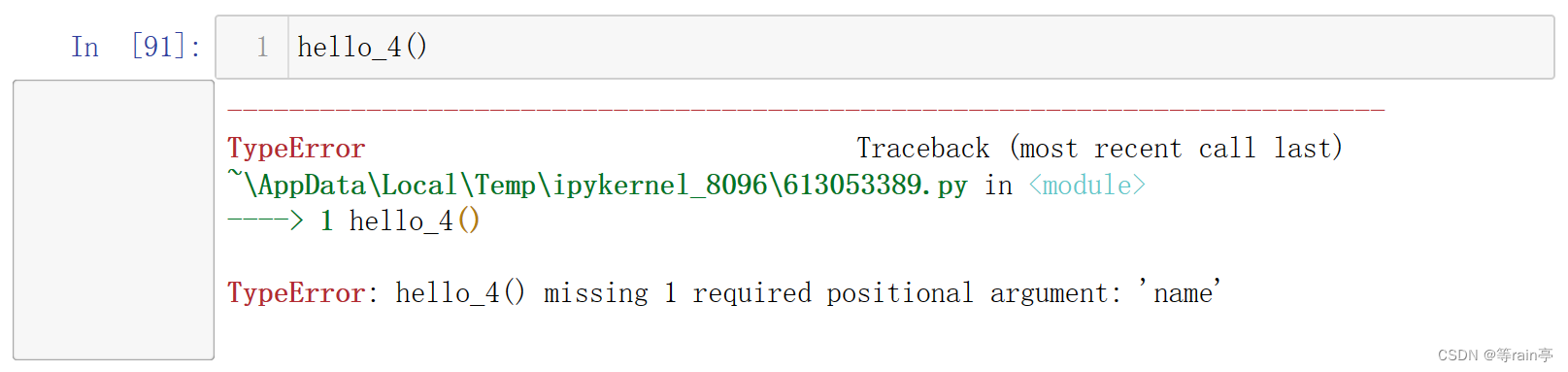
直接运行报错，因为name没有设定默认值。
6.4.4收集参数
有时候，允许用户提供任意数量的参数很有用。
每次只能存储一个数据太少了，如果可以同时存储多个数据就比较好：
为此，应允许用户提供任意数量的姓名。请尝试使用下面这样的函数定义：
这里好像只指定了一个参数，但它前面有一个星号。
看，我们引用这个定义，发现最终打印出的是一个元组，因为里面有一个逗号。那继续尝试是否可以打印出更多的项。
看出来，打印多个项目也是可以的。参数前面的星号将提供的所有值都放在一个元组中，也就是将这些值收集起来。这样的行我们在5.2.1节见过：赋值时带星号的变量收集多余的值。它收集的是列表而不是元组中多余的值，但除此之外，这两种用法很像。
和我们预期相同，第一个参数收集一个值（params），第二个参数由于有*号，所以收集剩余的值（1，2，3）。
这段代码，在第一个参数收集完第一个值，没有值了，所以第二个参数返回了一个空的元组。
那此时，我们可能会好奇，那如果说星号的参数在中间，它应该怎么判断剩余的元组呢？我们尝试一下：
星号不会收集管自己参数，如果不给z=6呢？
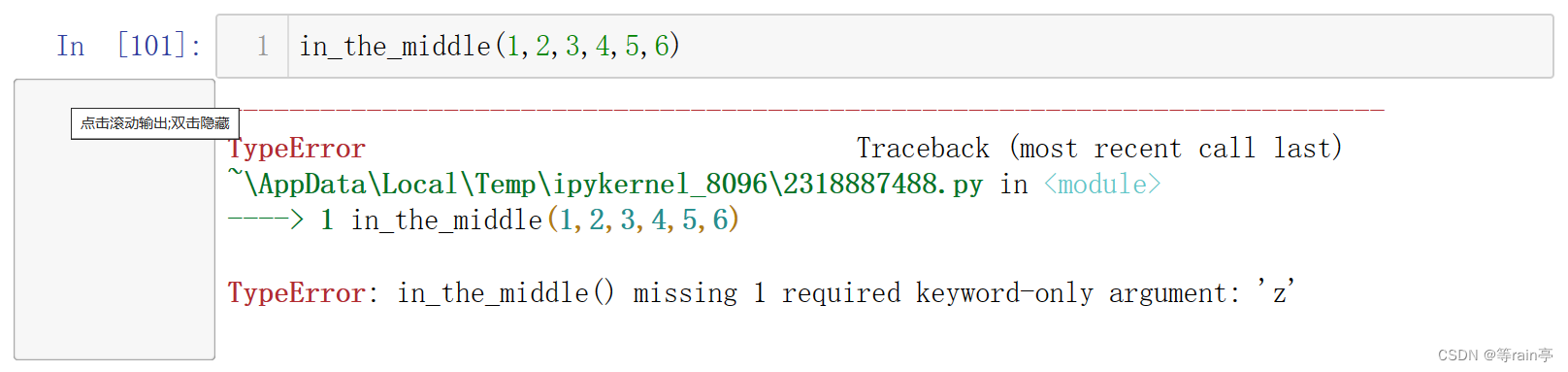
报错了。
星号不会收集关键字参数。如下。
正常来说，在参数title收集到Hmm...后，剩余内容被星号参数收集，但是事实上没有，因为提供了关键字了，星号不会收集关键字参数。
要收集关键字参数，可使用两个星号。
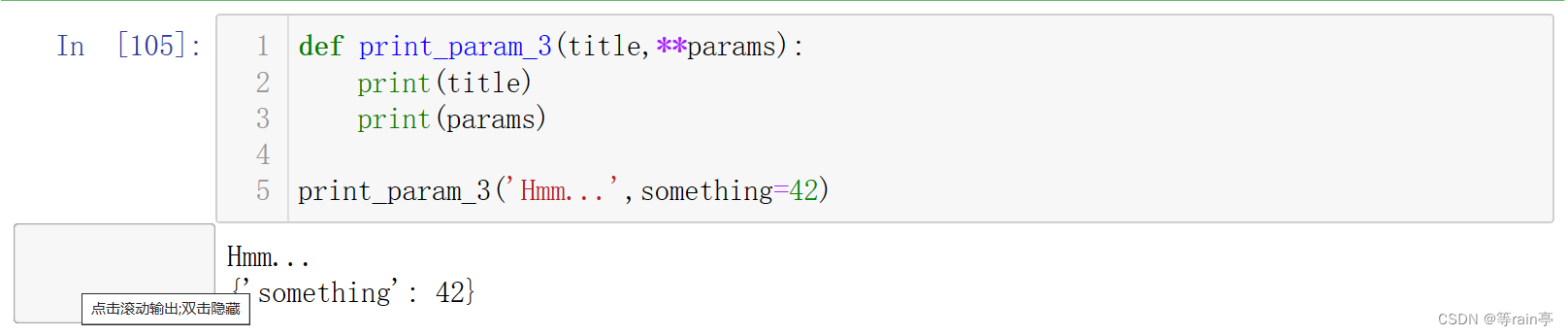
如你所见，这样得到的是一个字典而不是元组。
将以上的内容全部结合一下，位置，关键字，*，**
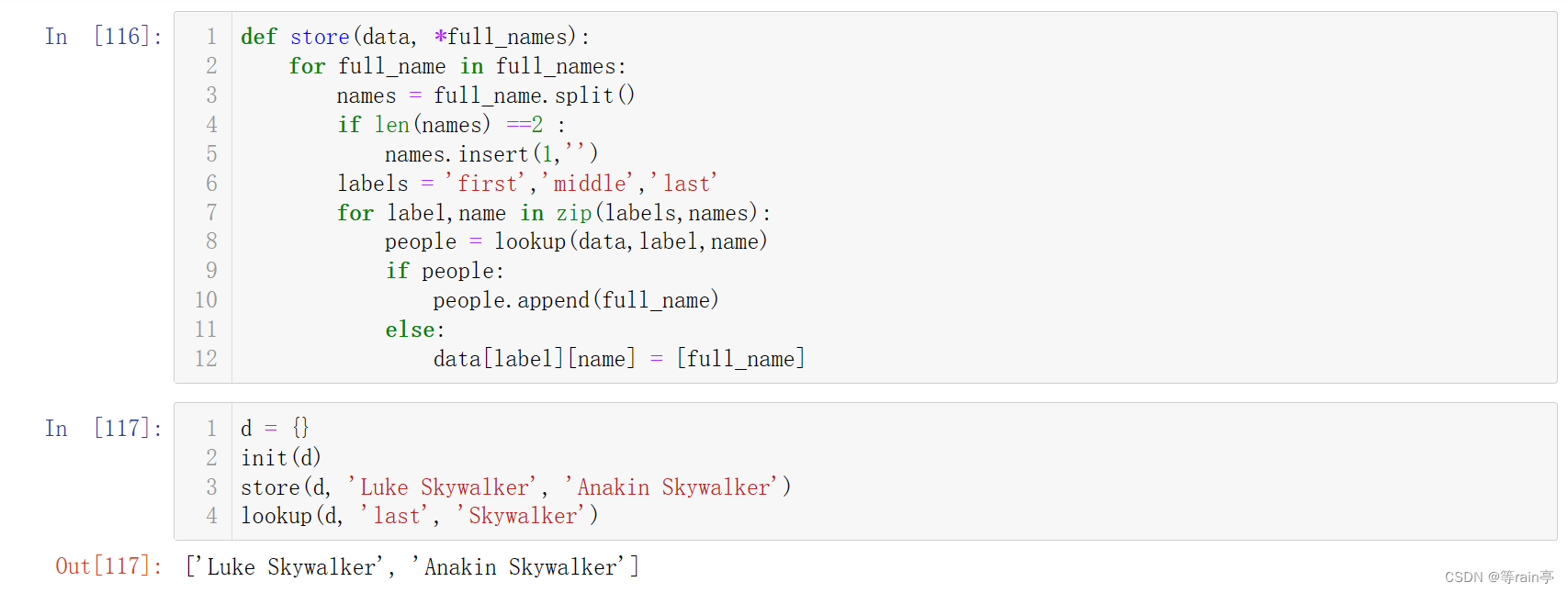
现在我们来解决最初的问题，如何在姓名存储示例中使用这种技术？解决方案如下：
6.4.5分配参数
前面介绍了如何将参数收集到元组和字典中，但用同样的两个运算符（*和**）也可执行相反的操作。与收集参数相反的操作是什么呢？假设有如下函数：
现在定义了一个相加的函数，但是给出的两个数据在一个元组里。现在就希望将这两个数据进行相加，但是定义中给的是两个参数。与收集参数相反的操作(不是收集参数，而是分配参数)：
当然使用一个*可以，也可以使用两个**。可将字典中的值分配给关键字参数。如下：
大家看下面这一段代码：
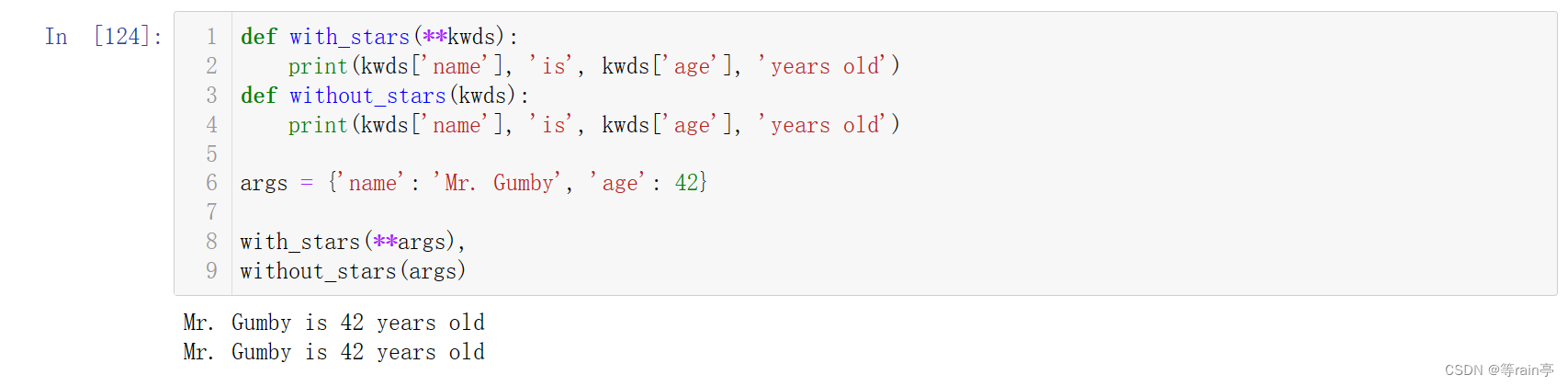
对于函数with_stars，我在定义和调用它时都使用了星号，而对于函数without_stars，我在定义和调用它时都没有使用，但这两种做法的效果相同。
因此，只有在定义函数（允许可变数量的参数）或调用函数时（拆分字典或序列）使用， 星号才能发挥作用。
使用这些拆分运算符来传递参数很有用，因为这样无需操心参数个数之类的问题，如下所示：
6.5作用域
变量到底是什么呢？可将其视为指向值的名称。因此，执行赋值语句x = 1后，名称x指向值1。这几乎与使用字典时一样（字典中的键指向值），只是你使用的是"看不见"的字典。
有一个名为vars的内置函数，它返回这个不可见的字典：
警告 一般而言，不应修改vars返回的字典，因为根据Python官方文档的说法，这 样做的结果是不确定的。换而言之，可能得不到你想要的结果。
这种"看不见的字典"称为命名空间或作用域。那么有多少个命名空间呢？除全局作用域外，每个函数调用都将创建一个。
这个地方就有些疑问了，我调用foo了，foo函数内赋值语句x=42，为什么最终x没有变化，依然是1呢？
这是因为调用foo时创建了一个新的命名空间，供foo中的代码块使用。赋值语句x = 42是在这个内部作用域（局部命名空间）中执行的，不影响外部（全局）作用域内的x。在函数内使用的变量称为局部变量（与之相对的是全局变量）。参数类似于局部变量，因此参数与全局变量同名不会有任何问题。
简而言之，就是创建函数foo时，创建了新的命名空间，这个空间里（局部）的x值不会影响到全局作用域中的x值。因此局部变量与全局变量同名也没有问题。
读取全局变量的值通常不会有问题，但还是存在出现问题的可能性。
（1）"遮盖"的问题
如果有一个局部 变量或参数与你要访问的全局变量同名，就无法直接访问全局变量，因为它被局部变量遮住了。(其实就是在局部变量里面使用全局变量时，如果局部变量中有与全局同名的，系统不知道识别哪一个，而因为在定义里面，会先访问局部变量)
那我到底如何让函数里知道我要访问全局变量呢？使用global
看，此时函数里就访问到了全局变量的parameter。
还记得我们在6.5开始的时候，函数里面的值的赋值操作，并没有改变函数外的值。那如何改变呢？
重新关联全局变量（使其指向新值）是另一码事。在函数内部给变量赋值时，该变量默认为局部变量，除非你明确地告诉Python它是全局变量。当然还是使用global。
ok,大家知道了可以这样进行关联全局变量。大家可以思考一下为什么下面这个x还是1呢？
（2）作用域嵌套
Python函数可以嵌套，即可将一个函数放在另一个函数内。
嵌套通常用处不大，但有一个很突出的用途：使用一个函数来创建另一个函数。这意味着可像下面这样编写函数：
在这里，一个函数位于另一个函数中，且外面的函数返回里面的函数。也就是返回一个函数，而不是调用它。重要的是，返回的函数能够访问其定义所在的作用域。换而言之，它携带着自己所在的环境（和相关的局部变量）！
每当外部函数被调用时，都将重新定义内部的函数，而变量factor的值也可能不同。由于Python的嵌套作用域，可在内部函数中访问这个来自外部局部作用域（multiplier）的变量，如下所示：
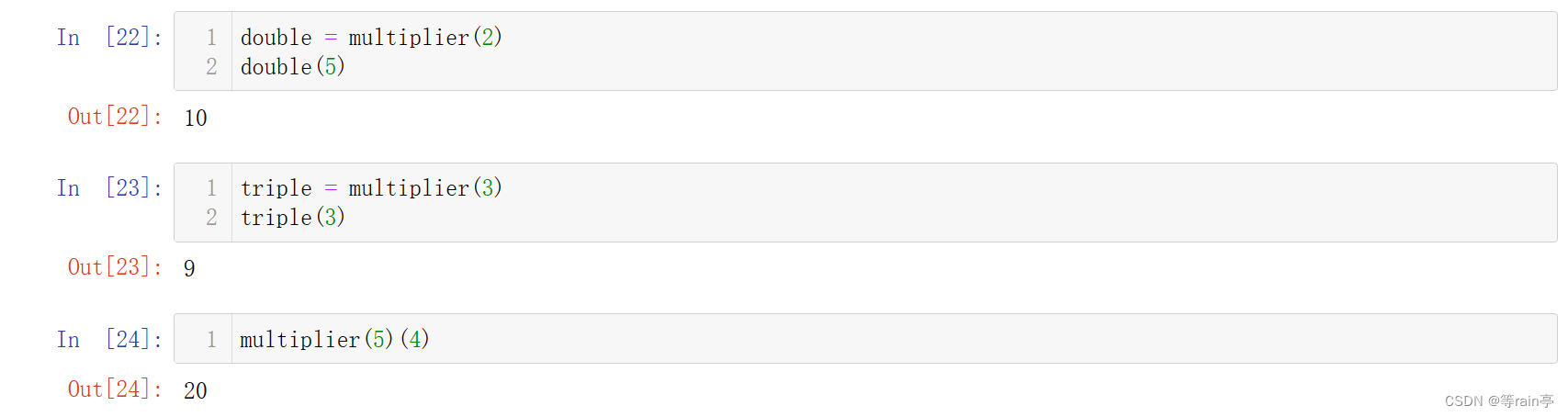
第一句中的2其实就是multiplier的factor，double中的5，其实就是number。下面两个例子也是类似的。
像multiplyByFactor这样存储其所在作用域的函数称为闭包。
通常，不能给外部作用域内的变量赋值，但如果一定要这样做，可使用关键字nonlocal。这个关键字的用法与global很像，让你能够给外部作用域（非全局作用域）内的变量赋值。
6.6递归
你知道，函数可调用其他函数，但可能让你感到惊 讶的是，函数还可调用自己。
如果你以前没有遇到这种情况，可能想知道递归是什么意思。简单地说，递归意味着引用（这里是调用）自身。（其实完全没有必要明白递归的准确定义）
这就是一个递归式函数的定义，其实什么都没做，与"递归"定义一样傻。
从理论上说，这个程序将 不断运行下去，但每次调用函数时，都将消耗一些内存。因此函数调用次数达到一定的程 度（且之前的函数调用未返回）后，将耗尽所有的内存空间，导致程序终止并显示错误消 息"超过最大递归深度"。
这个函数中的递归称为无穷递归（就像以while True打头且不包含break和return语句的循环被称为无限循环一样），因为它从理论上说永远不会结束。
我们需要的是对我们有帮助的递归，通常包含两个部分：
基线条件（针对最小的问题）：满足这种条件时函数将直接返回一个值。
递归条件：包含一个或多个调用，这些调用旨在解决问题的一部分。
6.6.1 阶乘与幂（经典案例）
首先，假设你要计算数字n的阶乘。n的阶乘为n × (n - 1) × (n - 2) × ... × 1，在数学领域的用途非常广泛。
首先将result设置为n，再将其依次乘以1到n - 1的每个数字，最后返回result。但如果你愿意，可采取不同的做法。
ok，上面这个方法就一步步的进行计算，但我们也可以采用不同的方法。
①1的阶乘为1。
②对于大于1的数字n，其阶乘为n - 1的阶乘再乘以n。这与阶乘的定义相同。
再来看一个示例。假设你要计算幂，就像内置函数pow和运算符**所做的那样。要定义一个数字的整数次幂，有多种方式，但先来看一个简单的定义：power(x, n)（x的n次幂）是将数字x自乘n - 1次的结果，即将n个x相乘的结果。
同样，也可以将他改成递归式。
①对于任何数字x，power(x, 0)都为1。
②n>0时，power(x, n)为power(x, n-1)与x的乘积。
提示 如果函数或算法复杂难懂，在实现前用自己的话进行明确的定义将大有裨益。以这种"准编程语言"编写的程序通常称为伪代码。
那么使用递归有何意义呢？难道不能转而使用循环吗？答案是肯定的，而且在大多数情况下，使用循环的效率可能更高。然而，在很多情况下，使用递归的可读性更高，且有时要高得多，在你理解了函数的递归式定义时尤其如此。
6.6.2二分查找
例如，对方心里想着一个1～100的数字，你必须猜出是哪个。当然，猜100次肯定猜对，但最少需要猜多少次呢？实际上只需猜7次。首先问："这个数字大于50吗？"如果答案是肯定的，再问："这个数字大于75吗？"不断将可能的区间减半，直到猜对为止。你无需过多地思考就能成功。
这样的想法适用于众多其他不同的情形。
一个常见的问题是：指定的数字是否包含在已排序的序列中？如果包含，在什么位置？为解决这个问题，可采取同样的策略："这个数字是否在序列中央的右边？"如果答案是否定的，再问："它是否在序列的第二个四分之一区间内（左半部分的右边）？"依此类推。明确数字所处区间的上限和下限，并且每一个问题都将区间分成两半。
这里的关键是，这种算法自然而然地引出了递归式定义和实现。
①如果上限和下限相同，就说明它们都指向数字所在的位置，因此将这个数字返回。
②否则，找出区间的中间位置（上限和下限的平均值），再确定数字在左半部分还是右 半部分。然后在继续在数字所在的那部分中查找。
在这个递归案例中，关键在于元素是经过排序的。找出中间的元素后，只需将其与要查找的数字进行比较即可
当然，上面的代码有一个缺陷，在一我们通常不知道lower和upper（这两个值代表的是列表的下标）所有可以进行修改。
现在进行调用，看是否正确。
结果是正确的，但是你可能会好奇，明明对于列表，我们可以直接index查找，为什么要这样呢？
的确，index是可以的，但是效率太低了，前面说过，要在100个数字中找到指定的数字，只需问7次；但使用循环时，在最糟的情况下需要问100次。（大家看100好像没什么，事实上，在可观察到的宇宙中，包含的粒子数大约为10 87个。要找出其中的一个粒子，只需问大约290次！）
实际上，模块bisect提供了标准的二分查找实现。