一 什么是匈牙利匹配算法
匈牙利算法是一种解决二分图最大匹配问题的算法。在二分图中,将左边的点称为X集合,将右边的点称为Y集合,我们需要在X集合和Y集合之间建立一个双向边集合,使得所有的边都不相交。如果我们能够找到一个最大的匹配,即所有点都能够被匹配,那么这个最大匹配的边数就是二分图的最大匹配。
匈牙利算法的基本思路是通过增广路径来寻找增广路,从而实现匹配的更新。具体来说,我们从一个未匹配的点开始遍历,对于每一个未匹配的点,我们都尝试找到一个与之相邻的未匹配点,如果找到了,就将这两个点匹配起来。如果找不到,我们就从这个点的相邻已匹配点中选择一个进行搜索,直到找到一个未匹配点或者搜索到底部为止。
二 一个关于匈牙利算法的例子
假设有如下一个实际问题。这里有n份工作任务,有n个工人,每个工人完成工作所需的成本不同(可以时间成本,可以是经济成本),但是由于每个工人在同一时间只能做一个工作,每个工作因此只能分配给一个工人,需要给出一个算法,求出总的花费成本最低。
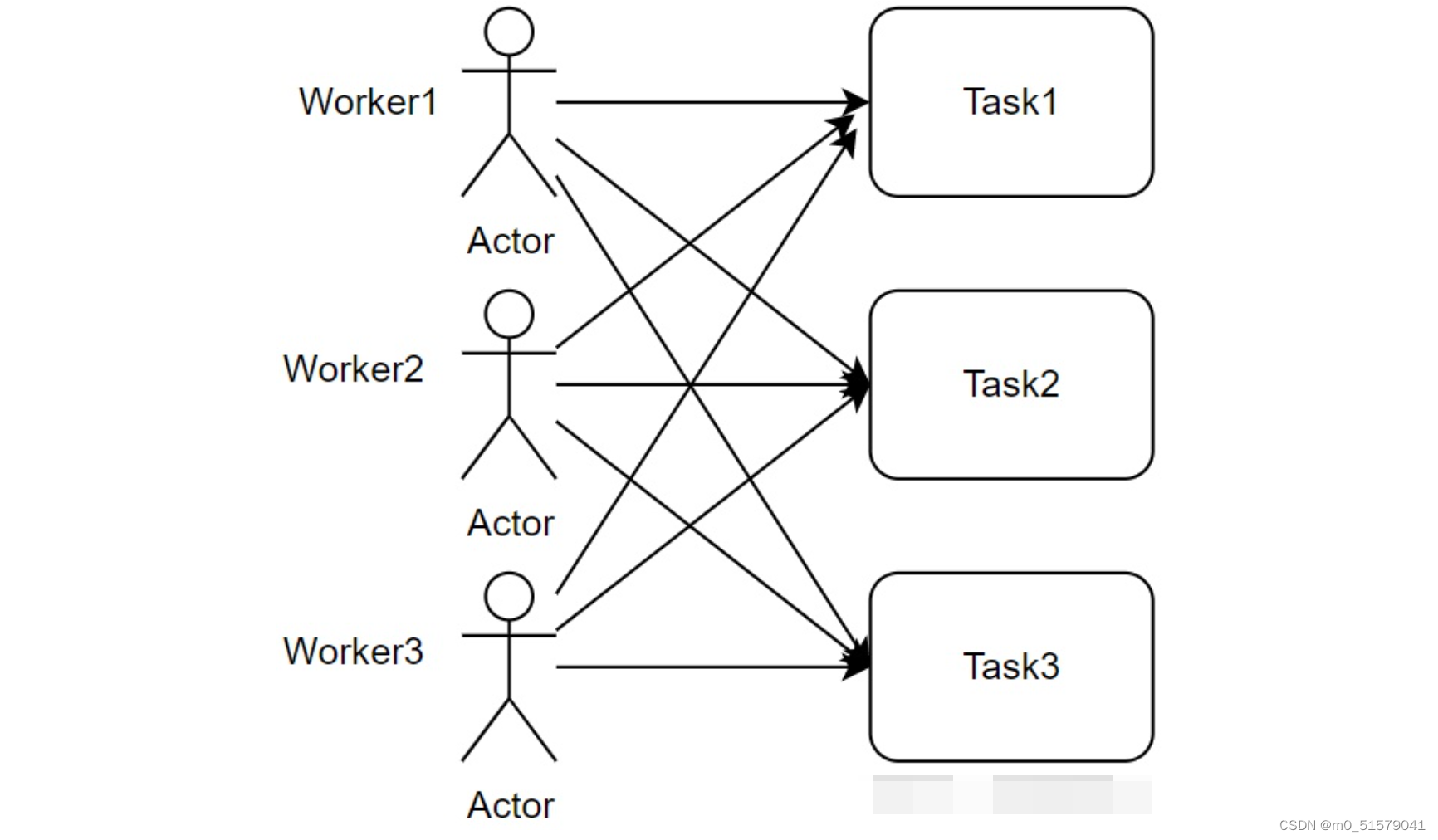
下面介绍其实现流程:
(1)创建cost matrix

那么上面这个表格或者说是矩阵,的第(i,j)个元素的值就对应着第i个工人分配给他第j个任务的成本。因此上面这个矩阵也就称为代价矩阵。
(2)每一行减去本行最小值

(3)每一列减去本列最小值

(4)用最少的直线划去所有的0,如果使用的直线数量(这里为2)等于K(这里为3),就跳到第(5)步,列出最优匹配;否则,跳到第(6)步,继续操作。

(5)列出最优分配(目前还没满足条件)。找到最优分配的过程可以表述为。依次找到只有一个0的元素,确定第一个最优匹配结果。然后,删除行和列,再找剩下的只有一个0的元素,确定第二个最优匹配结果,然后第三个就是剩下的最优匹配结果。
(6)找出没被直线划去的数中的最小值(这里为2)。
6.1 所有没有被直线完全划去的行减去该最小值

6.2 所有被直线完全划去的列加上该最小值

继续重复执行第(4)步,得到下面的结果

这个时候,直线数量(这里为3)等于K(这里为3)了,所以可以跳到第(5)步。
确定第一个最优匹配结果:
此时,第二行只有一个0元素,所以确定work2对应task3。

确定第二个最优匹配结果:
将上一步的第二行的0元素的所在行和列删除掉。

此时,第三行只有一个0元素,所以可以确定work3对应task1
确定第三个最优匹配结果:
继续将上一步的第三行的0元素的所在行和列删除掉。

此时,第一行只有一个0元素,所以可以确定work1对应task2
所以,上述的代价矩阵的最终最优分配矩阵为:

三 匈牙利匹配算法如何在目标检测跟踪中使用(deepsort)为例
在目标跟踪中,当前帧的检测器会生成Bounding Boxes的坐标位置和类别信息,而上一帧的跟踪器会进行预测生成Bounding Boxes的坐标和位置信息。两者如何一一配对呢?这就用到了之前的匈牙利匹配算法。
比如生成了一个有关于检测器Detections和跟踪器Tracks的代价矩阵。

其中这里面的元素都是通过距离计算处理出来的,具体有余弦距离,欧氏距离和IOU距离,前两个用于第一次匹配,IOU距离用于第二次匹配。
def gated_metric(tracks, dets, track_indices, detection_indices):
'''
根据外观信息和马氏距离,计算卡尔曼滤波预测到的tracks和当前时刻检测到的
detections的代价矩阵
'''
features = np.array([dets[i].feature for i in detection_indices])
targets = np.array([tracks[i].track_id for i in track_indices])
#基于外观信息,计算tracks和detections的余弦距离代价矩阵
cost_matrix = self.metric.distance(features, targets)
#基于马氏距离,过滤掉代价矩阵中的一些不合理的项,将其设置为一个较大的值
cost_matrix = linear_assignment.gate_cost_matrix(
self.kf, cost_matrix, tracks, dets, track_indices,
detection_indices)
return cost_matrix上述代码用来根据指定的方式(余弦距离,欧式距离,IOU距离),计算用于匈牙利算法的代价矩阵,然后利用马马氏距离修正。其中的features是经过re-ID后的Bounding Boxes的特征向量,包含了类别信息。track_id是对应根据上一帧预测到当前帧的跟踪Tracks。