文章目录
第一题
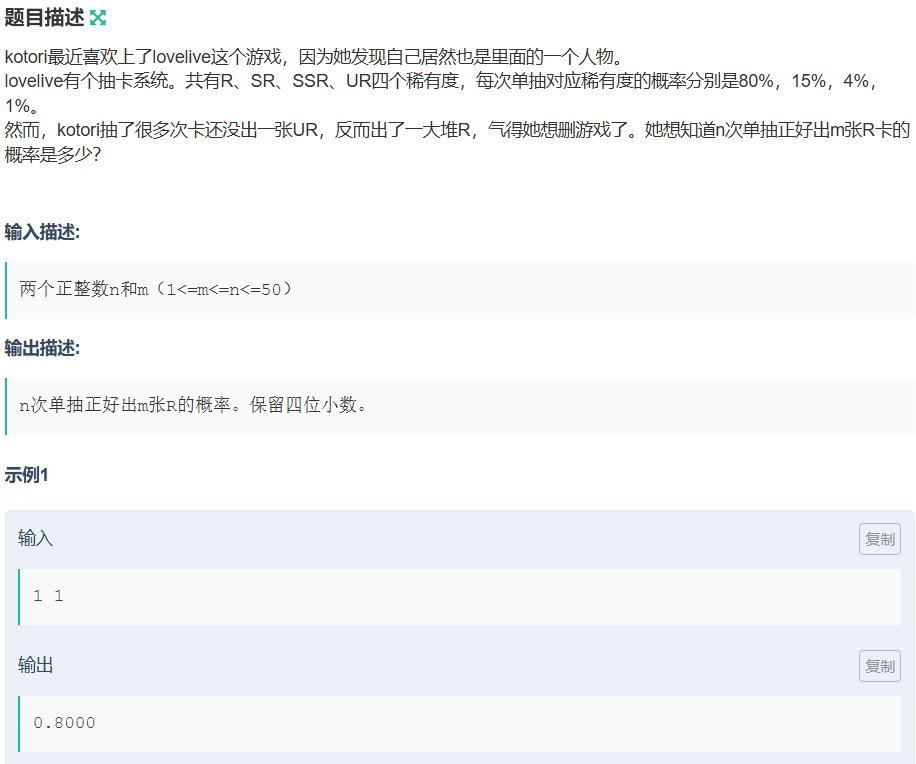
题目
思路
数学: 二项分布
C(n, m) * p ^ n * (1 - p) ^ m
代码
cpp
#include<iostream>
using namespace std;
int n, m;
int main()
{
cin >> n >> m;
double res = 1.0;
for(int i = n; i >= n - m + 1; i--) res *= i;
for(int i = m; i >= 1; i--) res /= i;
for(int i = 0; i < m; i++) res *= 0.8;
for(int i = 0; i < n - m; i ++) res *= 0.2;
printf("%.4f\n", res);
return 0;
}第二题
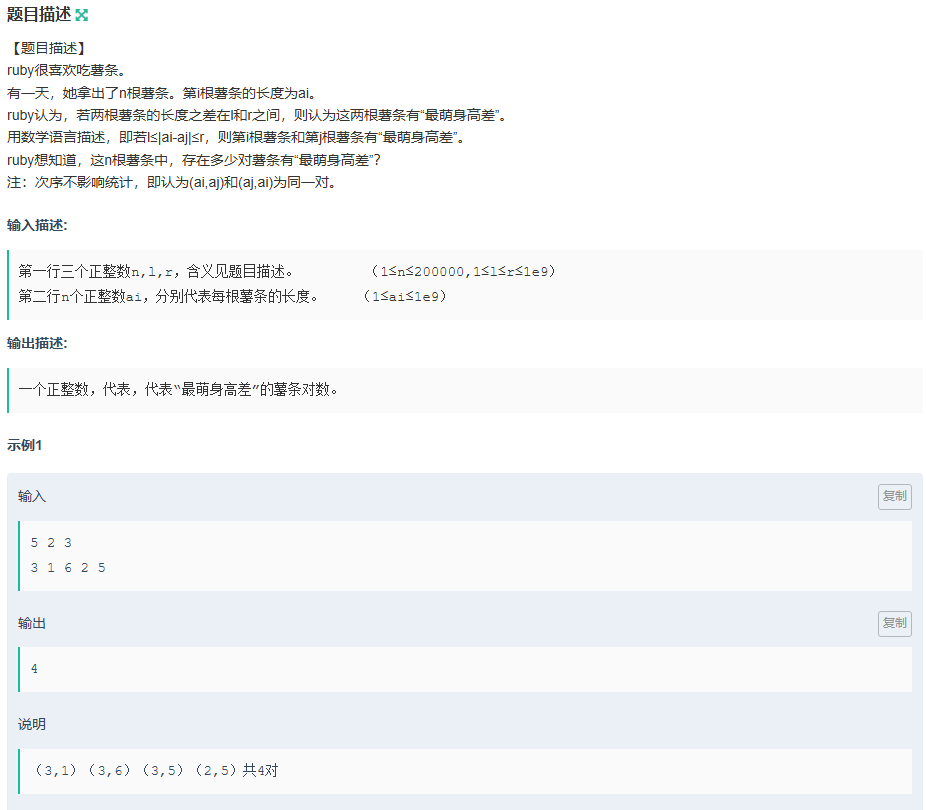
题目
思路 1
- 排序数组:首先对数组进行排序
- 遍历每个元素作为基准:对于每个元素a[i],寻找所有满足条件的a[j]
- 使用二分查找确定范围
- 找到第一个 ≥ a[i] + l 的位置(左边界)
- 找到第一个 > a[i] + r 的位置(右边界)
- 统计对数:两个边界之间的元素个数就是满足条件的对数
代码1
cpp
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 200010;
int n, l, r;
int a[N];
int main() {
cin >> n >> l >> r;
for (int i = 0; i < n; i++) cin >> a[i];
sort(a, a + n);
long long res = 0;
for (int i = 0; i < n - 1; i++)
{
int left_bound = a[i] + l;
int right_bound = a[i] + r;
// 找到第一个大于等于left_bound的位置
int j = lower_bound(a + i + 1, a + n, left_bound) - a;
// 找到第一个大于right_bound的位置
int k = upper_bound(a + i + 1, a + n, right_bound) - a;
res += (k - j);
}
cout << res << endl;
return 0;
}思路2
[l, r]之间⼀共有多少对等价于[0,r] - [0, l -1]有多少对- 利用滑动窗口解决
[0, x]有多少对;
代码2
cpp
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 200010;
int n, l, r;
int a[N];
// 找出差值在 [0, x] 之间⼀共有多少对
long long solve(int x)
{
long long res = 0;
int left = 0, right = 0;
while(right < n)
{
while((a[right] - a[left]) > x) left++;
res += right - left;
right++;
}
return res;
}
int main()
{
cin >> n >> l >> r;
for (int i = 0; i < n; i++) cin >> a[i];
sort(a, a + n);
cout << solve(r) - solve(l - 1) << endl;
return 0;
}第三题
题目

思路
模拟找规律
代码
cpp
#include <iostream>
using namespace std;
const int MOD = 1000000007;
int n;
int main()
{
cin >> n;
int x = 1, y = 2;
for(int i = 2; i <= n; i++)
{
int xx = 2 * y % MOD + 1;
int yy = (2 * y % MOD + 2 + x) % MOD;
x = xx;
y = yy;
}
cout << x << " " << y << endl;
return 0;
}
// 64 位输出请用 printf("%lld")