1.6 目标识别
利用检测和跟踪在距离、多普勒和角度这两个维度中的任意一个进行精确的目标定位后，将检测到的目标分类到所需的类别中。与检测类似，提出了多种框架来同时使用图像和点云进行目标分类。使用图像进行目标分类的最常见方法是从检测到的目标特征中沿距离-角度和距离-多普勒维提取手工设计的特征[32-34]。最常见的特征是距离、多普勒、到达方向的平均值，以及从唯一目标簇中检测到的所有峰值的归一化反射功率。此外，在特征集中增加了距离、径向多普勒和目标尺寸在x、y维度上的方差和偏差，增加了目标特征的丰富度。对于固定的网格大小，可以在检测到的目标区域上使用加速鲁棒特征(SURF)或尺度不变特征变换(SIFT)等特征描述符来替代手工制作的特征。然后，这些特征集可以传递给线性或非线性分类器，如决策树、支持向量机(SVM)或K近邻(KNN)。这种方法对传感器测量非常特别，并且容易产生噪声，因此，通常很难在不同位置或不同增益模式下对传感器的不同测量进行归纳。替代的最先进的方法涉及深度学习算法。后续将介绍引人注目的深度学习架构。
1.6.1 前馈网络
前馈神经网络或多层感知机(MLP)近似某个函数f，该函数f进行映射y = f(x;𝑤)，并学习网络的权重𝑤，从而在给定特定目标的情况下得到函数逼近。这些模型被称为前馈，因为信息流从x开始流经被评估的函数，通过用于定义f的中间计算，最后到达输出y。没有反馈连接，其中模型的输出被反馈到自身。图1.10给出了一个具有一个隐藏层的前馈网络。
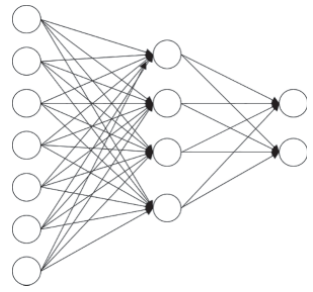
图1.10 有一个隐藏层的前馈神经网络示例
1.6.2 卷积神经网络（CNN）
在深度学习文献中，使用最广泛的网络是CNN[35-37]，用于目标检测、人脸识别、图像分割或超分辨等任务。在CNN中，图像分类是通过结合不同的层进行的，即卷积层、池化层和具有交叉熵(CE)损失的密集层。网络将图像视为维度为h ×𝑤× c (h =高度，𝑤=宽度，c =颜色通道)的多维像素数组。例如，尺寸为32 × 32 × 3的图像表示RGB图像(三色通道)，而尺寸为32 × 32 × 1的图像表示灰度图像。
CNN的初始空间特征提取是通过卷积层完成的。在卷积层中，滤波器或核(权矩阵)在整个图像中滑动。卷积层的输出被定义为滑动核与每个滑动步的底层输入图像的点积。必须注意的是，滤波器必须具有与输入图像相同数量的通道。
卷积层的输出维数计算如下:
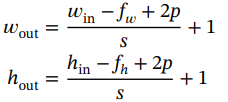（1.35）
其中，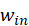
，
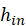是输入图像的宽度和高度，
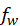和
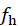是滤波器或内核的宽度和高度，p，s是为填充因子和跨步因子，设为≥1。网络通过反向传播来学习滤波器的权重。卷积层的组成描述如下:
1.步进:当应用卷积时，移位是为了在整个图像上移动滤镜。步幅定义了移动的步长，例如，如果步幅是1，那么过滤器移动一个像素，如果步幅是2，那么它移动两个像素，以此类推。
2.填充:当过滤器不能正确匹配输入图像时，有两个选项:
●零填充-用零填充图像，使滤镜完美匹配。
●有效填充-删除图像中不适合过滤器的部分
- 激活函数:在CNN中使用的一些标准激活函数如下:
●Sigmoid(逻辑激活):这个激活功能最初是受到"真实神经元"的启发。这个激活函数的输出在[0,1]之间。它的主要缺点是饱和的神经元无法学习，并且激活的计算成本很高。
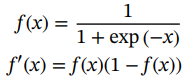（1.36）
●双曲正切激活:双曲正切激活的输出范围在[−1,1]之间，以零为中心。与乙状体激活类似，这种激活也不会训练饱和神经元。
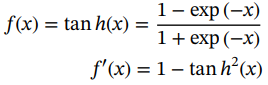（1.37）
●整流线性单元(ReLu):在ReLu激活中，如果x > 0，则不存在饱和，并且计算效率更高，收敛速度更快。在这种激活中，输出总是正的，不活跃的神经元没有被优化:
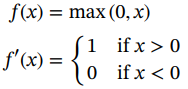（1.38）
●泄漏整流线性单元和参数ReLu:这些激活函数是对正常ReLu的改进，克服了神经元死亡的问题。对于泄漏的Relu， α是一个很小的常数，例如0.01。在参数化ReLu的情况下，α是通过反向传播学习的超参数。
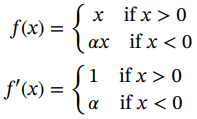（1.39）
图1.11给出了上述常用的激活函数，即sigmoid函数、双曲函数、整流线性单元(ReLu)和泄漏整流线性单元。
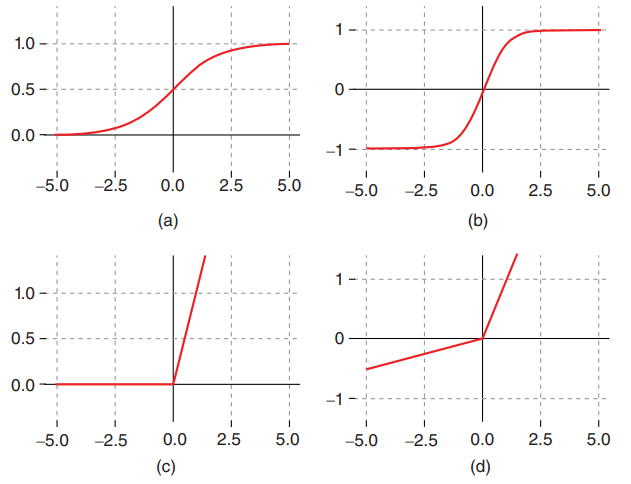
图1.11 各种激活函数示意图:(a) sigmoid函数，(b)双曲函数，(c) ReLu函数，(d) 泄漏ReLu。
用于分类问题的输出层中通常使用的另一个标准激活函数是softmax层。由于平方误差不适用于类相互排斥的情况，因此更好的方法是将输出之和为1的约束分配给每个类的概率。softmax函数强制输出表示可能类L之间的概率分布，其函数及其导数如下所示:
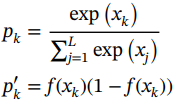（1.40）
通常与softmax层相关的代价函数是正确预测的负对数似然，称为CE或对数损失代价函数，定义如下:
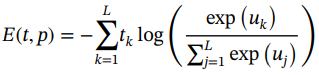（1.41）
4.池化/子样本层:池化层或更具体的空间池化层在保留最相关信息的同时对输入图像执行子采样或下采样。当图像太大时，这个过程有助于减少参数。
三种常用的池化层如下:
●最大池化-在定义的非参数过滤器大小中取最大的元素。
●平均池化-在定义的非参数过滤器大小内取所有元素的平均值。
●总和池化 -取定义的非参数过滤器大小内所有元素的和。
5.密集/完全连接层:在CNN的最后，使用单个或多个密集层，将先前卷积和池化层的扁平(1D数组)输出馈给这些层。在用于分类的CNN中，最后一个激活函数通常是sigmoid或softmax激活。
图1.12展示了一个CNN架构的例子，它包括卷积层、池化层或子样本层，然后是后期的密集或全连接层。
图1.12 一个CNN架构的例子
1.6.3 循环神经网络（RNN）
MLP和CNN不能直接解决信息随时间传播的问题。手势感应和跟踪等一些应用需要神经网络保存过去事件的历史来做出决定。RNN解决了这个问题，通过具有自循环结构，允许信息随时间持续存在。使用这些自循环，RNN能够将之前的信息与当前任务联系起来，并根据之前的事件做出决定。在20世纪90年代，阻碍RNN广泛应用的最大障碍之一是梯度消失的问题。不仅信息会随时间流动，而且误差也会随时间反向传播。为了做到这一点，自循环随着时间展开，这导致了一个非常深的网络，其中梯度必须通过许多层传播。但是，如果权重小于1，那么进一步乘以同样小于1的梯度，经过几次乘法后得到的结果将非常小。因此，随着时间的推移，通过RNN的梯度流很容易变为零，这意味着没有进一步的信息传播。结果，RNN无法保留信息或学习很久以前的信息。
RNN可以描述如下:RNN将给定的时间输入序列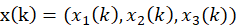
映射到隐藏值序列
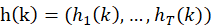，并通过迭代以下递归方程输出激活序列
:
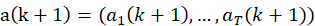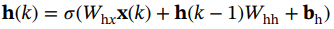（1.42）
其中σ是非线性激活函数，
是隐藏层偏移向量，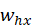
是输入隐藏权重
是隐藏-隐藏权重矩阵。
这些循环单元的激活定义如下:
(1.43)
其中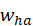
表示隐藏激活权重矩阵，
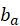表示激活偏移向量。
RNN存在梯度消失或爆炸的问题，这可以通过长短期记忆(LSTM)[38]或门控循环单元(GRU)[39]来解决。LSTM使用门控的概念扩展带有记忆单元的RNN:门控是一种基于输入的组件乘法的机制，它定义了每个单独记忆单元的行为。LSTM根据门的激活更新它的单元状态。提供给LSTM的输入被送入不同的门，这些门控制在单元存储器上执行的操作:写(输入门)、读(输出门)或复位(忘记门)。这些门根据它们接收到的信号，通过它们自己学习到的滤波器权重，根据信号的强度和重要性来阻止或传递信息。这些权重是在反向传播期间学习的，这意味着单元格的权重决定何时允许输入、保留或删除数据。
LSTM层更新的向量表示(向量表示一层中的所有单元)如下:
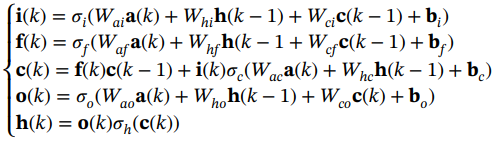(1.44)
其中i，f，o和c分别为输入门，忘记门，输出门和单元激活向量，它们的大小都与定义隐藏值的向量h相同。项σ表示非线性激活函数。项{x(1)， x(2)，···，x(K)}是时刻K的存储单元层输入。Wai, Whi,Wci, Waf, Whf, Wcf, Wac, Whc, Wao, Who和Wco是权重矩阵，下标表示从属关系，bi, bf, bc和bo是偏置向量。
图1.13展示了LSTM块的一个单元。根据应用程序的不同，有不同的配置来使用RNN模型。RNN不仅可以将一个输入映射到一个输出，还可以将一个输入映射到多个输出，多个输入映射到一个输出或多个输入映射到多个输出。
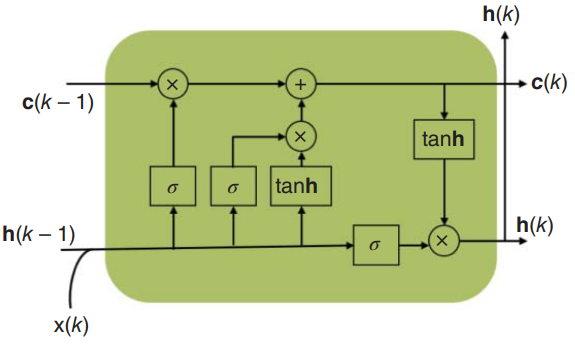
图1.13 一个LSTM单元例子
这四种配置如图1.14所示。多对一配置用于雷达手势感知，多对多配置用于人体活动分类。
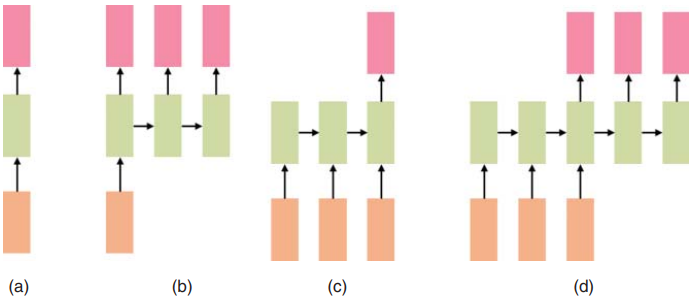
图1.14 不同类型的RNN模型:(a)一对一，(b)一对多，(c)多对一，(d)多对多。