摘要
本研究提出了一种新的方法来重建代表大脑动力学的功能网络,该方法基于两个脑区在同一认知任务中的共同参与会导致其可识别性或其动力学特性降低的观点。这种可识别性是通过深度学习模型在监督分类任务中获得的分数来估计的,因此不需要对这种协同参与的性质进行先验假设。该方法在阿尔茨海默病和帕金森病患者以及匹配的健康志愿者的睁眼和闭眼静息态EEG信号上进行了测试,并通过标准拓扑度量对所得的功能网络进行了分析。两组患者都表现出相应脑电信号的可识别性降低,以及支持这种可识别性的模式存在差异。生成的功能网络与使用相关性指标重建的功能网络相似,但并非完全相同。控制组与患者之间的差异可以在不同网络指标(如聚类系数和同配性)以及不同频段中观察到。睁眼和闭眼条件之间也存在显著差异,特别是对于帕金森病患者。
引言
尽管经过了几十年的实验和理论研究,但在复杂认知任务甚至简单的静息态条件下,大脑活动背后的原理和机制仍然难以捉摸。提高我们对大脑理解的一个可能途径是网络神经科学,即通过网络表征大脑活动,其中节点代表不同的大脑区域,并且每当检测到相应区域之间存在信息传播时,这些节点就会相互连接。这种方法具有整合性,因为元素根据它们的连接性进行表征,并将实证数据采集与计算方法相结合,因此该方法处于生物医学和计算机科学的交叉领域。最重要的是,它对不同病理如何影响正常的大脑动态提供了开创性的见解。
这种网络方法的一个基本假设是,两个或多个脑区共同参与计算任务,导致相应脑区的动态具有一些共同的特征。换句话说,脑区在孤立状态下具有独特的动态,但通过参与任务(例如,通过共享一些信息),这些不同的动态变得更加相似。通过线性相关性重建功能网络就是一个最简单的例子,预期不同脑区之间具有相关幅度,从而展现出共同的特征。当使用更复杂的指标时(比如因果关系或同步指标),也会做出类似的假设。换句话说,重建功能网络类似于检测新出现的(广义)相似性。
本文探讨了一种相反的方法,即如何将认知任务的共同参与检测为所涉及的大脑区域动态的独特性下降。换句话说,类似于标准的功能网络重建假设,本研究假设脑区在功能上是同质的,并且具有独特的动力学特征;然而,在执行共同的认知任务时,这种独特性在一定程度上会减弱。因此,本研究不再专注于检测相似性的增加,而是将焦点转向独特性的减少。这种方法远非单纯的语义转换,它具有两个重要优势。首先,它不对脑区动力学的共同特征做出假设,比如相关性、相位等等。相反,任何能够减少动力学独特性的共同特征都会被考虑在内,前提是我们有方法来检测这种减少。其次,这种方法可以被定义为一种分类任务,即训练一个机器学习模型来识别来自两个脑区记录的时间序列;分类得分越高,两个区域就越独特(或可识别),因此它们参与相同认知任务的次数就越少。这使我们能够借助深度学习(DL)模型,即最先进的机器学习算法,无需假设或数据先验结构,而且非常敏感,能够检测数据集之间微妙而复杂的差异。
虽然DL模型在神经科学领域并不陌生,但本研究方法在两个主要方面有所不同。首先,分类模型并不用于实际分类。相反,分类任务的得分用于评估每组数据的独特性,也就是其可识别性。其次,分类的结果并非孤立使用,而是基于网络表征的更复杂分析中的一步。因此,分类不是目的,而是分析的工具。通过将该方法应用于帕金森病(PD)和阿尔茨海默病(AD)患者以及对照组的EEG静息态记录数据集,探讨了这种方法的可能性和局限性。
材料与方法
参与者
本研究招募了50名参与者,根据其健康状况分为三组:阿尔茨海默病(AD)和帕金森病(PD)患者,以及健康的老年对照组。参与者的人口统计信息如表1所示。所有参与者均接受完整的神经系统检查、结构磁共振成像(MRI)、常规实验室筛查以及一系列神经心理学测试。
表1.人口统计信息。

EEG数据记录
使用Brain Products BrainAmp 32通道DC系统记录EEG数据,采样率为500Hz。使用EasyCap与32 Ag/AgCl电极按10/20系统放置,所有电极阻抗均保持在10kΩ以下。使用A1和A2电极作为参考电极(耳垂)。为了记录眼电图(EOG),使用了两个Ag/AgCl电极,分别放置在左眼眶上缘和外侧缘。所有被试的EEG记录包含4分钟的睁眼和4分钟的闭眼数据(即每个被试的每个通道约有240000个数据点)。在睁眼记录期间,要求被试注视黑屏。在整个EEG记录期间,研究人员使用摄像头对被试进行监测。
用于时间序列分类的深度学习模型
本研究重点关注时间序列分类模型,即给定一组时间序列,每个序列都有一个标签(即它所对应的EEG通道),目标是为呈现给算法的新时间序列分配正确的标签。文献中已经提出了几种用于这一任务的模型,通常由图像分类模型演变而来(有关完整的综述和相应的源代码,请参阅https://github.com/hfawaz/dl-4-tsc)。更具体地说,使用了以下五种模型。
多层感知器(MLP)。它是神经网络最传统和最简单的形式之一,由一组按层组织的节点组成,每个节点从前一层接收信息,并通过非线性激活函数做出响应。尽管MLP模型不编码时间信息,但它已被提出作为时间序列分类的基准架构。这里考虑的网络由四层组成,每层都与前一层的输出完全连接,最后一层是softmax分类器。激活函数是众所周知的整流线性单元(ReLU)。
卷积神经网络(CNN)。卷积网络是MLP的变体,其中矩阵乘法用卷积运算代替。它们的优点包括空间(或者在时间序列情况下,时间)不变性,以及减少过拟合的倾向。在这里,本研究采用一个简单的卷积模型,包括两个卷积层和一个Sigmoid分类器。
残差网络(ResNet)。残差网络的灵感来自大脑皮层中锥体细胞的组织方式;具体而言,层与层之间的连接不是连续的,而是可以跳过某些层。这样做的好处是简化了结构,因此减少了训练成本。这里考虑的网络由11个层组成,前9层是卷积层,然后是一个全局平均池化层,该层对整个时间维度的时间序列进行平均,最后是一个softmax分类器。
全卷积神经网络(FCN)。FCNs是一种只执行卷积运算的网络。该模型由三个卷积块组成,每个块都执行卷积、批量归一化和激活。最后,第三个卷积块的结果被输入到softmax分类器中。
多通道深度卷积神经网络(MCDCNN)。该模型是基于改进的CNN,其中卷积独立地(并行地)应用于输入多变量时间序列的每个维度(或通道)。由于这里只考虑单变量数据,即每个EEG通道由单个时间序列表示,因此MCDCNN和CNN的结果虽然并不总是相同,但可能会相似。
分类任务和可识别性
给定同一组中(对照组、阿尔茨海默病和帕金森病患者)所有被试的一对EEG通道的时间序列,通过DL模型的最佳分类分数对这两个通道的可识别性进行评估。在分类问题的每次迭代中,时间序列被分成1000个数据点的非重叠段(相当于2s)。可用时间序列的随机一半用于训练,剩下的一半用于模型评估,因此相当于二折交叉验证。最终通过相应的准确率分数来衡量每个模型的性能,即正确分类片段所占的比例;需要注意的是,由于使用了完全平衡的数据集,其他指标(例如召回率或F分数)在这里是多余的。为了清晰起见并避免与同名的复杂网络指标混淆,这里将效率称为分类分数,或者在简称为分数。
功能网络重建与分析
在复杂网络理论中,一个网络由大小为N×N(其中N为节点数)的邻接矩阵A定义,其中元素ai,j在连接节点i和j时设为1,否则设为0。在网络神经科学背景下,当传感器i和j对应的时间序列之间计算得到的同步指标(例如,相关性)大于给定阈值时,ai,j被设置为1,这表明存在一种共享的动态。如前所述,这里提出的方法是相反的:由于共享动态会导致这两个传感器的可识别性降低,因此当这种可识别性(通过相应的分类分数来衡量)低于阈值时,将添加一个连接。也就是说,分类分数越低,相应脑区之间的连接就越强。
一旦这些网络被重建,它们就会被二值化,也就是说,强度超过给定阈值的连接将被保留,其他的则被删除。这是网络神经科学中的一种标准方法,可以减少弱连接的影响。本文采用一种比例阈值法,在每个网络中包含固定数量的最强连接。这种方法通常被称为密度或网络成本保持不变的分析,并被认为有利于病例对照研究。
结果
比较DL模型
首先通过比较不同深度学习模型获得的分数来分析结果;如前所述,这些模型基于不同的架构并检测数据中的不同模式,因此预计它们会产生异质的结果。对于三组被试,图1报告了每对EEG通道中获得最佳分数的模型。可以看出,模型以非随机方式分布,一些模型与某些脑区的较高分数相关。不同脑区具有不同的活动模式,这些模式更容易被某些模型识别。此外,三组之间存在差异,表明两种病理情况进一步改变了局部动态。
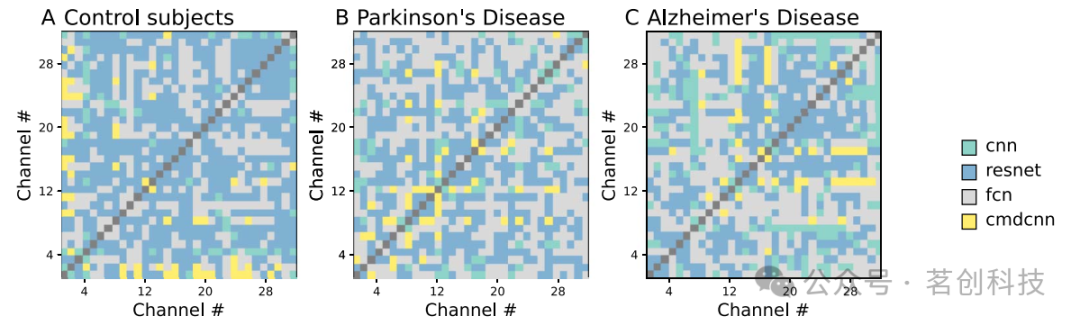
图1.四种DL模型的比较。
EEG通道对的可识别性
然后分析了每对EEG通道的可识别性。具体来说,图2顶部的三个图显示了每对通道在三组中获得的平均分类分数。请注意,在本文的其余部分,对于给定的EEG通道对,所报告的分类分数与最佳DL模型产生的分数相对应。结果表明,三组中的连接性共享相同的基础结构,并且受到传感器之间串扰的强烈影响。为了突出与条件相关的模式,底部的三个图显示了每对条件之间(两组之间)在通道对上的可识别性差异。这种差异主要表现为一些特定的EEG通道中存在的模式。总的来说,与对照组相比,AD患者的可识别度明显降低;在PD患者中,下降程度相对较轻。
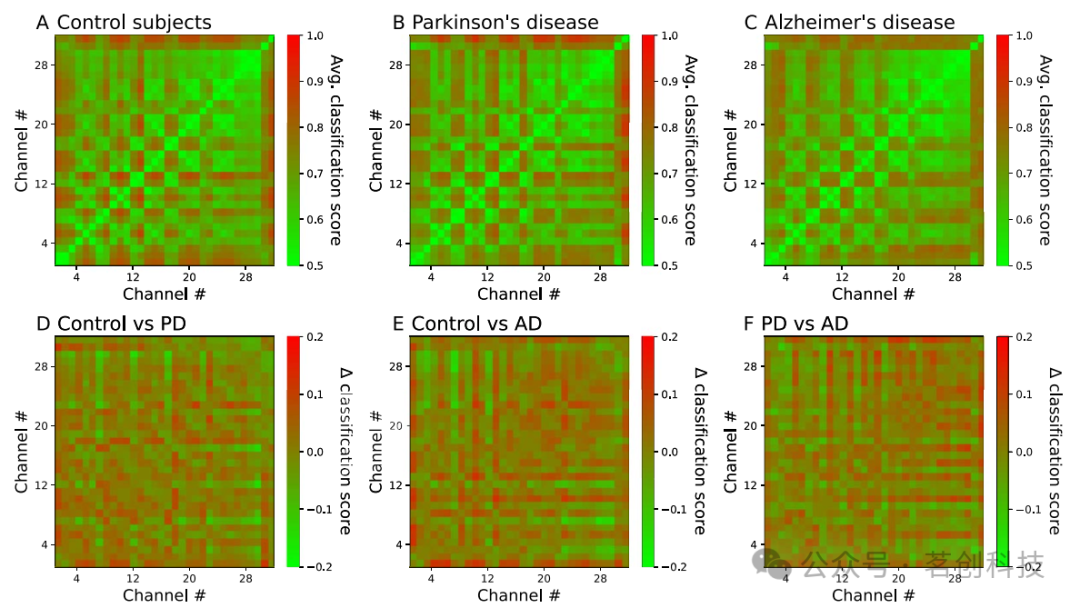
图2.EEG通道对的可识别性。
本研究进一步分析了这种成对可识别性的另外两个方面。首先,人们可能会问,可识别性(这里定义为分类任务产生的分数)与更传统的功能指标之间有什么关系。为了回答这个问题,图3报告了三个散点图(每个条件一个散点图),即每对EEG通道之间的Pearson线性相关性的平均绝对值,作为相应分类分数的函数。正如预期的那样,可以观察到普遍的负相关;换言之,高度相关的通道由于动态相似而更难被识别,从而具有较低的可识别性。然而,这两个指标并不相同;弱相关的时间序列可以产生高和低的分类分数,这表明深度学习模型可以检测到更复杂的模式。举例来说,如果两个时间序列具有相似的动态特性但具有不同的特征频率,即使它们的相关性很低,它们也很容易被识别。另一方面,两个非常复杂的时间序列也可能是弱相关的,并且识别其独特模式也将是一项具有挑战性的任务。
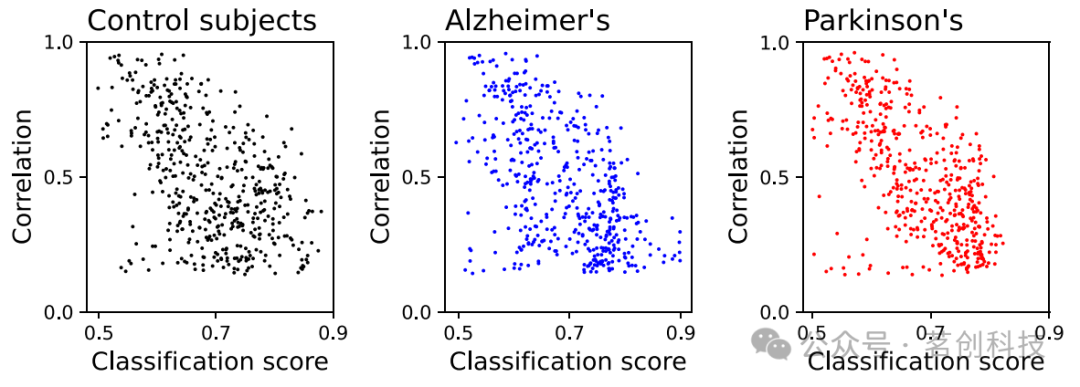
图3.线性相关与分类分数。
其次,本研究分析了时间序列的可识别性与频率信息的关系。具体而言,在图4的顶图中报告了每种条件的分类分数直方图,以及宽频信号和四个滤波频段:α(8-13Hz)、β1(13-20Hz)、β2(20-30Hz)和γ(30-50Hz)。此外,该图的底图报告了三种条件和五个频段的中位分类分数。宽带时间序列始终更容易被识别;每种条件下都可以观察到一些细微差异,例如,PD患者和β2频段的可识别度下降。
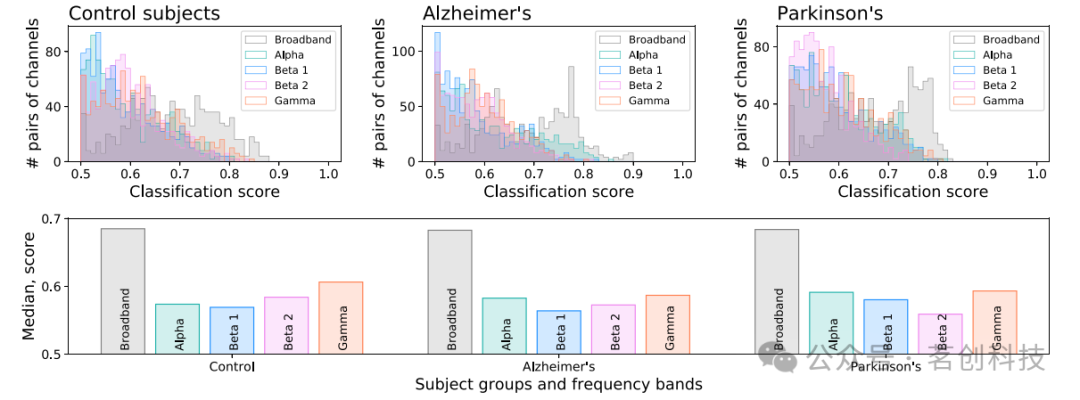
图4.可识别性和频率信息。
网络分析
重建功能网络的常用方法包括对EEG信号对进行成对比较,从而得到每个被试的功能网络。然后,可以对这些网络,以及从这些网络中提取的拓扑指标,在多个患者之间进行平均,以获得给定条件的全局图像。α频段和β1频段的聚类系数,以及宽频信号和β1频段的同配性如图5所示。为了评估这些结果的显著性,灰色区域报告了相同指标在10-90百分位数范围内的数值,基于所有三组时间序列的功能网络重建的零模型获得;每个子图内的插图进一步报告了每组指标的Z分数(根据该零模型计算得出)随时间的变化情况。从图中还可以观察到各组之间的一些差异。例如,AD组在α频段的聚类系数更高,但在β1频段较低;相比于PD,AD在宽频信号和β1频段上具有更大的同配性。
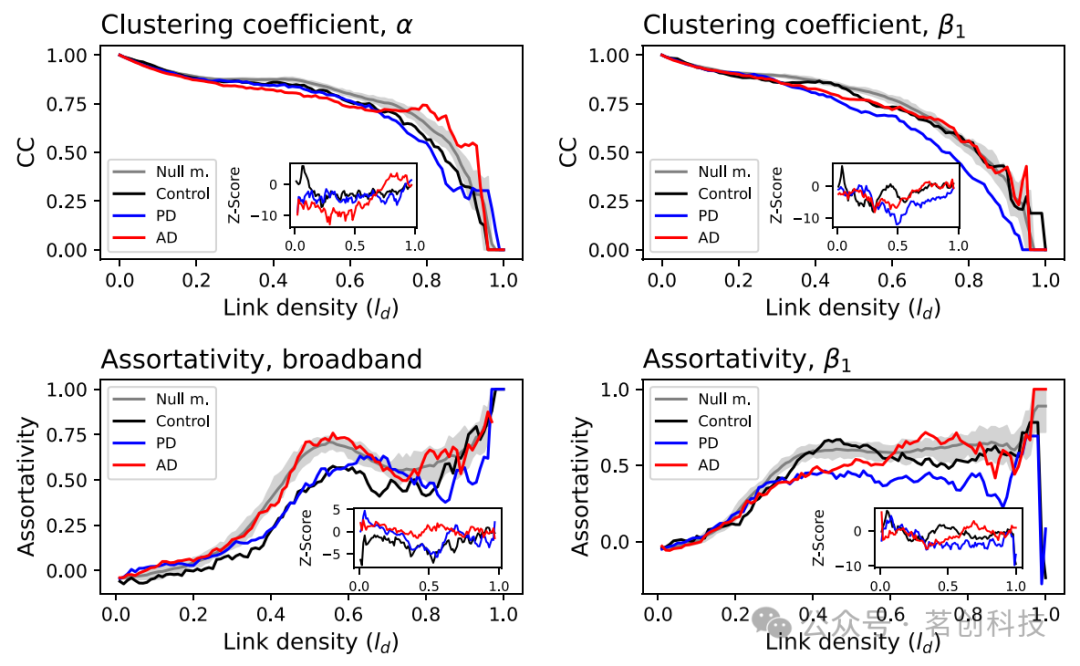
图5.拓扑指标示例。
本研究进一步分析了这些拓扑指标如何受到被试者睁眼或闭眼状态的影响。图6说明了两个拓扑指标的演变情况;顶图对应于原始指标数值,而底图对应于使用零模型计算的Z分数,即与图5中的插图相同。可以观察到一些大致趋势,比如PD患者闭眼和AD患者睁眼的差异较大:前者(后者)的聚类系数和同配性最小(最大),但嵌套性最大(最小)。
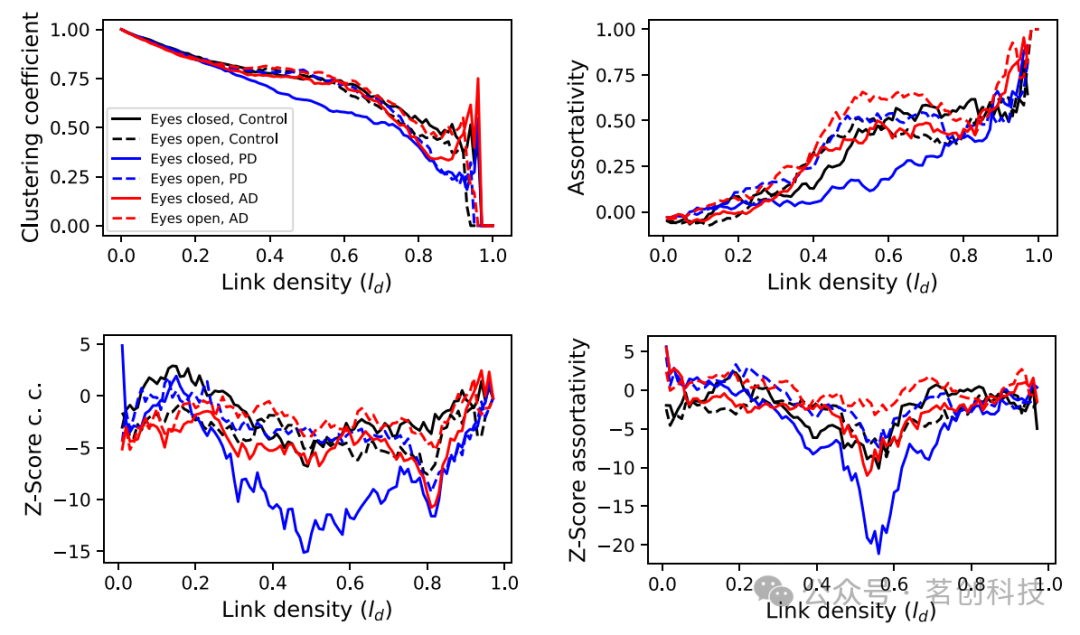
图6.睁眼和闭眼条件的比较。
结论
本研究提出了一种分析神经影像信号的新方法,该方法基于对每个脑区动态的可识别性或"独特性"的评估。这种方法无需先验地假设必须分析时间序列的哪些方面来检测相似性,而是关注使时间序列(或一组时间序列)具有独特性的任何动态方面。这使我们能够借助深度学习(即最先进的机器学习模型)进行分析。最终结果可用于检测认知任务中脑区协同参与所导致的动力学损失,从而为重建脑功能网络提供一种新的方法。
参考文献:Zanin, M., Aktürk, T., Yıldırım, E., Yerlikaya, D., Yener, G., & Güntekin, B. (2024). Reconstructing brain functional networks through identifiability and deep learning. Network Neuroscience, 8(1), 241--259. https://doi.org/10.1162/netn_a_00353
小伙伴们关注茗创科技,将第一时间收到精彩内容推送哦~