Title
题目
CLIK-Diffusion: Clinical Knowledge-informed Diffusion Model for ToothAlignment
CLIK-Diffusion:用于牙齿矫正的临床知识感知扩散模型
01
文献速递介绍
正畸治疗旨在矫正牙齿错位(即错颌畸形),为错颌问题提供了有效的解决方案。据估计,超过56%的人存在不同程度的错颌问题(Stomatologic,2020),且大多数人能从正畸干预中获益。这种治疗不仅能增强患者的自信心和心理健康,还能保护患者的口腔健康并预防口腔疾病(Grewal等,2019;Geiger,2001)。牙齿矫正是正畸治疗中的关键阶段,其目标是从一组错位牙齿中预测出理想的牙列状态。然而,传统流程需要繁琐费力的手动操作,且严重依赖牙医的专业经验,导致治疗效率低下、疗程延长。 随着数字技术的快速发展,已有多种计算机辅助方法被提出用于自动化正畸治疗,致力于解决上述挑战。Lingchen等(2020)提出了一种名为TAligNet的轻量级模型,但该模型仅使用基于多层感知器(MLP)的网络来回归每颗牙齿的姿态,结果较为平庸。Wei等(2020)基于PointNet(Qi等,2017)和图神经网络提出了一种牙齿排列网络TANet,旨在直接回归牙齿的变换矩阵。Lei等(2024)引入了一种基于视觉Transformer的扩散模型U-ViT(Bao等,2023),称为TADPM,通过MeshMAE(Liang等,2022)利用全牙列点云的全局特征和牙齿网格的局部特征,预测每颗牙齿的6自由度旋转和3D平移。Deng等(2024)提出了名为TAPoseNet的框架,该框架采用DGCNN(Wang等,2019)估计牙齿的初始姿态,最终通过MLP回归每颗牙齿的目标姿态。然而,这些方法均未整合临床先验知识,只是简单学习两种状态之间的映射关系,导致结果的临床适用性有限。在将临床知识融入牙齿矫正方面,与我们最接近的研究是TANet+(Wang等,2022),它是基于其先前TANet的扩展研究。具体而言,TANet+保持了相似的网络结构,但引入了牙齿地标点作为细粒度约束,以使牙齿保持正常倾斜。尽管如此,现有方法仍存在两个主要局限性:(1)基于点云的方法(如PointNet或DGCNN)或基于网格的方法(如MeshMAE)天然难以捕捉牙齿的细粒度局部结构和空间关系;(2)矫正结果与临床知识的契合度不够高。 为解决上述局限性,本文提出了**CLIK-Diffusion(临床知识感知扩散模型)**,一种用于自动牙齿矫正的临床知识融合扩散模型。首先,我们为牙齿矫正任务引入了一种新的表述方式。如图1所示,我们不再使用点云表示结合PointNet进行变换矩阵回归任务,而是引入牙齿地标点表示结合生成模型来完成地标点生成任务。由专业牙医预先确定的牙齿地标点,能够在整个正畸过程中有效表征牙齿的位置、朝向和形状。由于我们的生成模型基于牙齿地标点表示构建,这为在标地标点层面整合关键临床知识创造了自然途径。受牙齿矫正的经验性临床规则(即**安德鲁六要素与六关键(Andrews,1972;LF,2000),这是实现正常咬合和确保正畸治疗成功的关键标准,详见2.3节)的启发,我们从三个维度设计了层级约束:(1)牙弓层面:从全局约束牙齿排列;(2)牙齿间层面:确保相邻牙齿紧密接触并避免不必要的碰撞;(3)单颗牙齿层面:保证每颗牙齿的正确朝向。通过这种方式,我们的CLIK-Diffusion能够预测出符合临床知识的正畸后地标点。一旦正畸后牙齿地标点被预测出来,结合其正畸前牙齿地标点,可使用Kabsch算法(Kabsch,1976)确定每颗牙齿的刚性变换。这些优化后的变换可应用于每颗牙齿,从而生成正畸后的牙列。我们在真实临床收集的多种错颌畸形病例上对所提方法进行了验证,实验结果表明,与最先进的方法相比,我们的方法性能更优。本文的贡献总结如下: 1. 我们提出了CLIK-Diffusion,这是首个用于牙齿矫正的生成模型,它引入了一种创新的表述方式(即地标点表示),实现了具有空间感知和形状感知能力的牙齿排列。 2. 我们的CLIK-Diffusion整合了从三个维度设计的层级约束:牙弓层面、牙齿间层面和单颗牙齿层面,这些约束均受临床实践中的经验规则启发。 3. 大量评估(包括对比实验、外部验证、消融研究和用户研究)表明,我们的方法能够预测出排列良好的结果,在定性和定量性能上均优于现有方法。这凸显了我们所提CLIK-Diffusion的有效性和临床应用能力。
Abatract
摘要
Traditional semi-automatic methods for tooth alignment involve laborious manual procedures and heavilydepend on the expertise of dentists, which often leads to inefficient and prolonged treatment durations.Although many automatic methods have been proposed to assist especially the less experienced dentists,they often lack incorporating clinical insight and oversimplify the problem by estimating rigid transformationmatrix for each tooth directly from dental point clouds. This over-simplification fails to capture nuancedrequirements of orthodontic treatment, i.e., specific clinical rules for effective alignment of misaligned teeth. Toaddress this, we propose CLIK-Diffusion, a CLInical Knowledge-informed Diffusion model for automatic toothalignment. CLIK-Diffusion formulates the complex problem of tooth alignment as a more manageable landmarktransformation problem, which is further refined into a landmark coordinate generation task. Specifically, wefirst detect landmarks for each tooth by category, and then build our CLIK-Diffusion to learn distribution ofnormal occlusion. To further encourage the integration of essential clinical knowledge, we design hierarchicalconstraints from three perspectives: (1) dental-arch level: to constrain arrangement of teeth from a global level;(2) inter-tooth level: to ensure tight contact and avoid unnecessary collision between neighboring teeth; and (3)individual-tooth level: to guarantee correct orientation of each tooth. In this way, our designed CLIK-Diffusionis able to predict the post-orthodontic landmarks that align with clinical knowledge, and then estimate rigidtransformation for each tooth based on coordinates of its pre- and post-orthodontic landmarks. We haveevaluated our CLIK-Diffusion on various malocclusion cases collected in real-world clinics, and demonstrate itsexceptional performance and strong applicability in orthodontic treatment, compared with other state-of-the-artmethods.
传统的半自动化牙齿矫正方法需要繁琐的手动操作,且严重依赖牙医的专业经验,这往往导致治疗效率低下、疗程延长。尽管已有许多自动化方法被提出以辅助经验不足的牙医,但这些方法通常缺乏对临床见解的整合,并且通过直接从牙齿点云中估计每颗牙齿的刚性变换矩阵来过度简化问题。这种过度简化无法满足正畸治疗的精细需求,即错位牙齿有效矫正所需的特定临床规则。 为解决这一问题,我们提出了CLIK-Diffusion(临床知识感知扩散模型),一种用于自动牙齿矫正的临床知识融合扩散模型。CLIK-Diffusion将复杂的牙齿矫正问题转化为更易于处理的地标点变换问题,并进一步细化为地标点坐标生成任务。具体而言,我们首先按类别检测每颗牙齿的地标点,然后构建CLIK-Diffusion模型以学习正常咬合状态的分布。为进一步促进关键临床知识的整合,我们从三个维度设计了层级约束:(1)牙弓层面:从全局层面约束牙齿排列;(2)牙齿间层面:确保相邻牙齿紧密接触且避免不必要的碰撞;(3)单颗牙齿层面:保证每颗牙齿的正确朝向。通过这种方式,我们设计的CLIK-Diffusion能够预测符合临床知识的正畸后地标点,进而基于每颗牙齿正畸前后的地标点坐标估计其刚性变换。 我们在真实临床收集的多种错颌畸形病例上对CLIK-Diffusion进行了评估,结果表明,与其他最先进的方法相比,该模型表现卓越,在正畸治疗中具有很强的适用性。
Method
方法
3.1. Problem formulation
Fig. 2 illustrates our algorithm pipeline. The set of initial toothmodels is symbolized as 𝑋𝑖𝑛𝑖𝑡𝑖𝑎𝑙 = {𝑋1 , 𝑋2 , ..., 𝑋𝑁}, where 𝑁 = 28represents the total number of teeth for a single patient. With these28 pre-orthodontic tooth models within a single dentition, we aim topredict the corresponding 28 post-orthodontic tooth models 𝑋̂ 𝑡𝑎𝑟𝑔𝑒𝑡 ={𝑋̂ 1 , 𝑋̂ 2 ,... , 𝑋̂𝑁 }, which would emulate the well-aligned teeth designedby experienced dentists.As mentioned in Section 2.2, existing methods adhere to traditional formulation that directly regresses transformation matrices fromextracted features. This approach necessitates the use of point cloudbased encoders for feature extraction, which often leads to loss ofspatial information related to the teeth. Furthermore, integrating clinical knowledge into the transformation regression process continues topose a significant challenge.Hence, in this paper, we propose a new formulation that convertsthe tooth alignment task into a more manageable task of landmark coordinate generation by the powerful diffusion model. Tooth landmarks,being more concise, are position- and orientation-aware representations, thereby improving efficiency and better fitting our task. To thisend, we first detect a few depictive landmarks for each tooth using alightweight neural network (see Section 3.2.1 and Fig. 2 left). It takes𝑋𝑖𝑛𝑖𝑡𝑖𝑎𝑙 as input and predicts 𝐿𝑖𝑛𝑖𝑡𝑖𝑎𝑙 = {𝐿1 , 𝐿2 , ..., 𝐿𝑁 }, where 𝐿𝑖 ∈𝐿𝑖𝑛𝑖𝑡𝑖𝑎𝑙* is the total landmarks of one tooth. Subsequently, we samplea fixed number of points surrounding landmarks for each individualtooth mesh to form the dentition descriptor, aimed to capture moreshape-aware features (Section 3.2.2 and Fig. 2 left). These landmarksand the dentition descriptor together serve as condition of our diffusionmodel, for which, we have designed hierarchical constraints inspiredby clinical knowledge to supervise the diffusion training (Section 3.3and Fig. 2 middle). Our diffusion model outputs the desired targetlandmarks 𝐿̂𝑡𝑎𝑟𝑔𝑒𝑡 = {𝐿̂ 1 , 𝐿̂ 2 , ... , 𝐿̂𝑁 }. Finally, with 𝐿𝑖𝑛𝑖𝑡𝑖𝑎𝑙 and 𝐿̂𝑡𝑎𝑟𝑔𝑒𝑡,we vote for a single transformation for each tooth with the helpof least square optimization and transform 𝑋𝑖𝑛𝑖𝑡𝑖𝑎𝑙 to produce 𝑋̂𝑡𝑎𝑟𝑔𝑒𝑡(Section 3.4 and Fig. 2 top right).
3.1. 问题表述 图2展示了我们的算法流程。初始牙齿模型集表示为\(𝑋_{initial} = \{𝑋_1, 𝑋_2, ..., 𝑋_N\}\),其中\(𝑁 = 28\)代表单个患者的牙齿总数。基于同一牙列中的这28个正畸前牙齿模型,我们旨在预测对应的28个正畸后牙齿模型\(\hat{𝑋}{target} = \{\hat{𝑋}1, \hat{𝑋}2, ..., \hat{𝑋}N\}\),使其能够模拟经验丰富的牙医设计的整齐牙齿状态。 如2.2节所述,现有方法遵循传统表述方式,直接从提取的特征中回归变换矩阵。这种方法需要使用基于点云的编码器进行特征提取,这往往会导致牙齿相关空间信息的丢失。此外,将临床知识整合到变换回归过程中仍然是一项重大挑战。 因此,在本文中,我们提出了一种新的表述方式,通过强大的扩散模型将牙齿矫正任务转化为更易于处理的地标点坐标生成任务。牙齿地标点更简洁,是具有位置和朝向感知的表示形式,从而提高了效率并更适合我们的任务。为此,我们首先使用轻量级神经网络为每颗牙齿检测若干标志性地标点(见3.2.1节和图2左侧)。该网络以\(𝑋{initial}\)为输入,预测初始地标点集\(𝐿{initial} = \{𝐿_1, 𝐿_2, ..., 𝐿_N\}\),其中\(𝐿_i \in 𝐿{initial}\)表示单颗牙齿的全部地标点。随后,我们为每个牙齿网格的地标点周围采样固定数量的点,形成牙列描述符,旨在捕捉更具形状感知的特征(3.2.2节和图2左侧)。这些地标点和牙列描述符共同作为我们扩散模型的条件,我们设计了受临床知识启发的层级约束来监督扩散模型的训练(3.3节和图2中间)。我们的扩散模型输出期望的目标地标点\(\hat{𝐿}{target} = \{\hat{𝐿}1, \hat{𝐿}2, ..., \hat{𝐿}N\}\)。最后,结合\(𝐿{initial}\)和\(\hat{𝐿}{target}\),我们借助最小二乘优化为每颗牙齿确定单一变换,并对\(𝑋{initial}\)应用该变换以生成\(\hat{𝑋}_{target}\)(3.4节和图2右上)。
Results
结果
We start by visualizing several test cases to demonstrate ourmethod's effectiveness, then compare it quantitatively and qualitativelywith existing methods. Subsequently, we conduct extensive ablationstudies to validate our proposed hierarchical clinical-inspired constraints and the dentition descriptor technique. Ultimately, user studiesare conducted to validate the clinical applicability of our proposedCLIK-Diffusion.
我们首先通过可视化多个测试案例来证明我们方法的有效性,随后从定量和定性层面将其与现有方法进行对比。接下来,我们开展了大量消融研究,以验证所提出的层级化临床启发约束和牙列描述符技术的有效性。最后,通过用户研究验证我们提出的CLIK-Diffusion的临床适用性。
Figure
图
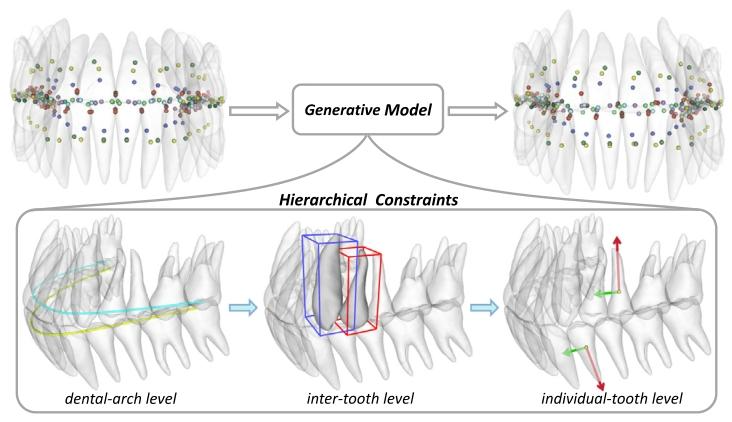
Fig. 1. Overview of our formulation. We formulate the complex tooth alignment taskas a more manageable landmark generation task. This is facilitated by a generativemodel which is guided by hierarchical clinically-inspired constraints.
图1 我们的方法框架概述。我们将复杂的牙齿矫正任务转化为更易于处理的地标点生成任务。这一过程由生成模型实现,该模型受层级化临床启发约束的引导。
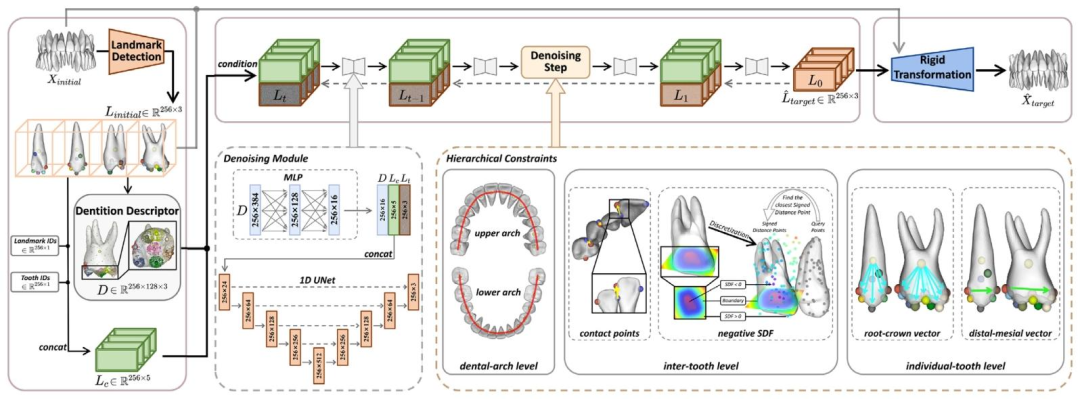
Fig. 2. Overview of our proposed CLIK-Diffusion. Given the pre-orthodontic dentition 𝑋**𝑖𝑛𝑖𝑡𝑖𝑎𝑙, we first detect all tooth landmarks and then sample points surrounding landmarks(Section 3.2), which then serve as condition for our diffusion model to predict the desired target landmarks (Section 3.3). Finally, we derive rigid transformations (Section 3.4) foreach tooth from the initial and predicted landmarks and apply them to 𝑋𝑖𝑛𝑖𝑡𝑖𝑎𝑙 to obtain the post-orthodontic dentition ̂𝑋*𝑡𝑎𝑟𝑔𝑒𝑡. Note that the left dashed box depicts the detailedstructure of our denoising module within the diffusion model, while the right dashed box illustrates the calculation process of hierarchical constraints.
图2 我们提出的CLIK-Diffusion框架概述。给定正畸前牙列(𝑋{initial}),我们首先检测所有牙齿的地标点,然后在地标点周围采样点(3.2节),这些信息随后作为扩散模型的条件,用于预测期望的目标地标点(3.3节)。最后,我们根据初始地标点和预测的目标地标点推导每颗牙齿的刚性变换(3.4节),并将这些变换应用于(𝑋{initial}),得到正畸后牙列(\hat{𝑋}_{target})。注意,左侧虚线框展示了扩散模型中去噪模块的详细结构,右侧虚线框则说明了层级约束的计算过程。
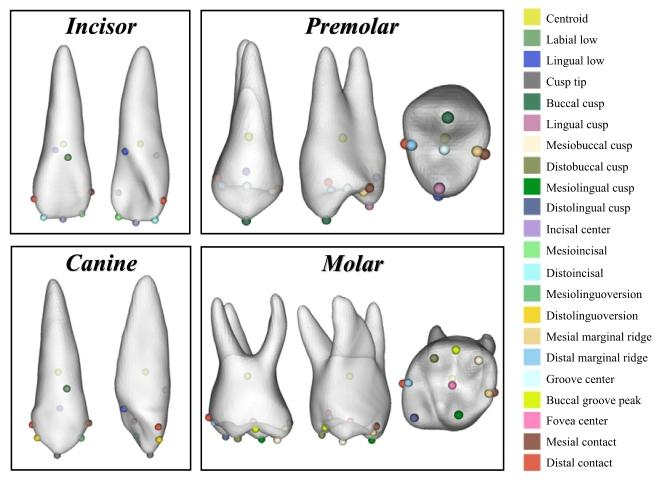
Fig. 3. Illustration of tooth landmarks for different types of teeth as defined byAndrews' Six Keys and dental experts. The landmarks are color-coded and labeled withtheir medical terms.
图3 基于安德鲁六关键及牙科专家定义的不同类型牙齿地标点示意图。地标点采用彩色编码并标注有其医学术语。
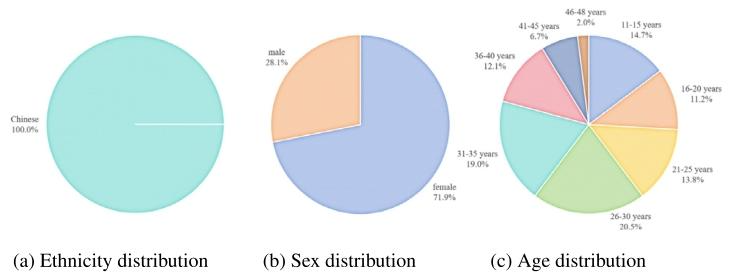
Fig. 4. Demographic information of our dataset
图4 我们数据集的人口统计学信息。
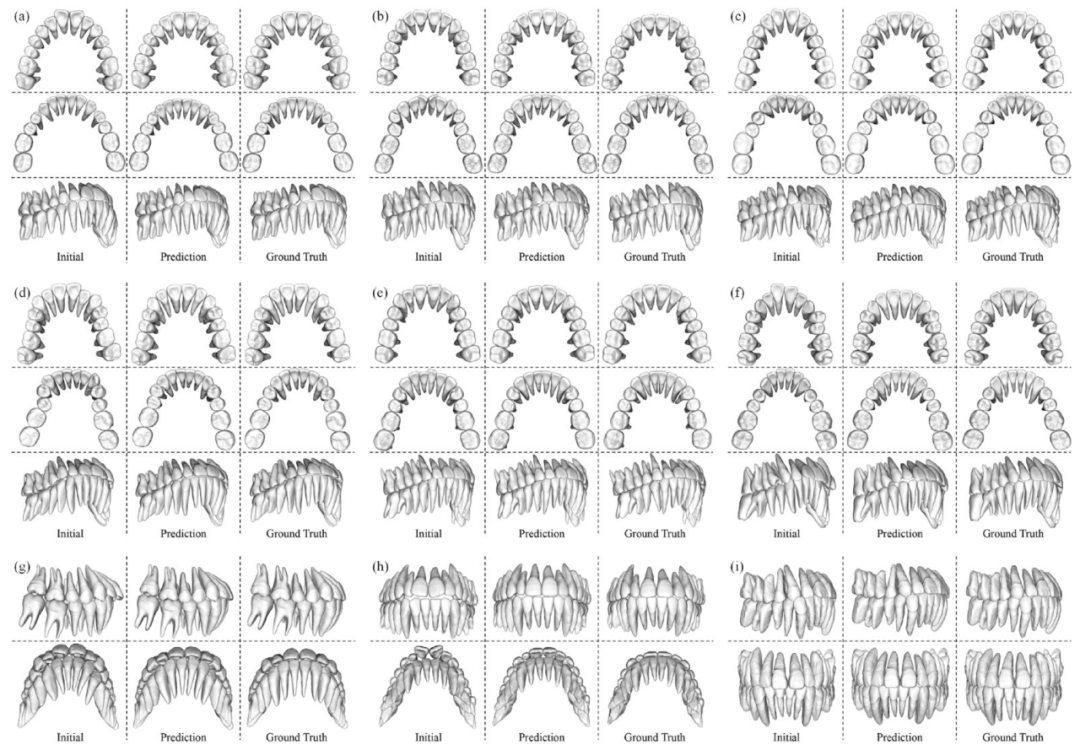
Fig. 5. Visualization of the results of our method. The layout for cases (a, b, c, d, e, f) features a uniform three-row format, where the upper, middle, and lower rows representthe upper teeth, the lower teeth and the side view, respectively. Cases (g, h, i) have a variable layout tailored to the specific case details. For all cases, the three columns fromleft to right depict the initial dentition, the prediction generated by our method, and the ground truth
图5 我们方法的结果可视化。案例(a、b、c、d、e、f)采用统一的三行布局,上、中、下三行分别代表上颌牙齿、下颌牙齿和侧视图。案例(g、h、i)的布局根据具体案例细节进行了调整。所有案例中,从左到右三列分别展示初始牙列、我们方法生成的预测结果以及真实结果。
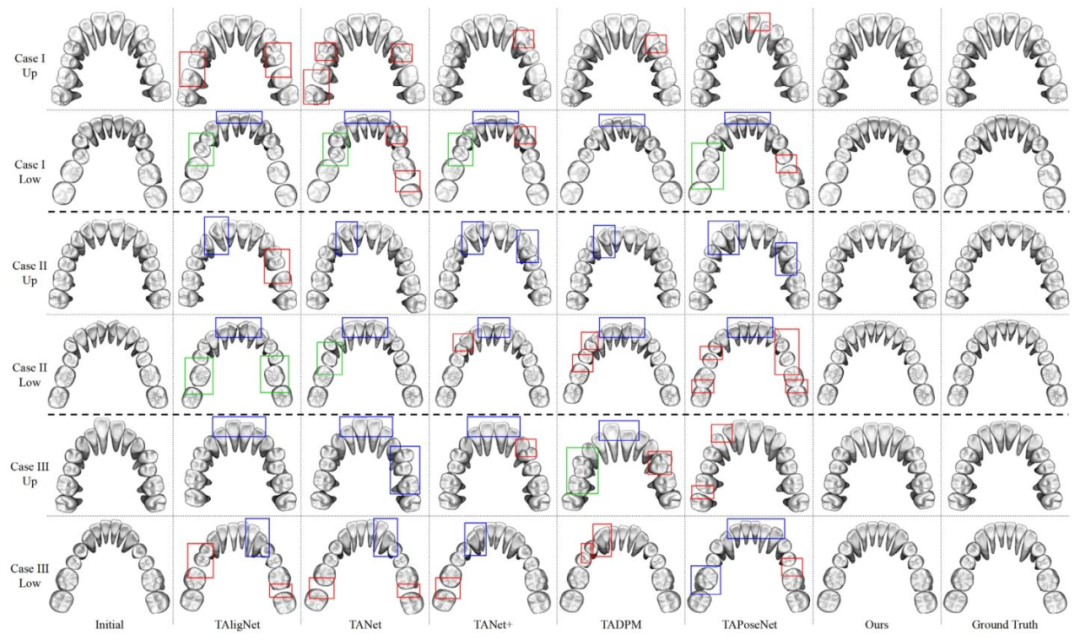
Fig. 6. Visualization of our comparative experiments with the other methods. Here, three cases are shown and each case is represented by two rows: the upper teeth above andthe lower teeth below. The red-boxed regions ( ) indicate instances of collision or excessive spacing issue between neighboring teeth, while the blue-boxed regions ( ) indicateinstances of improper orientation of the teeth. The green-boxed regions ( ) indicate instances of improper position of the teeth resulting in the irregular dental arch.
图6 我们与其他方法的对比实验结果可视化。此处展示了三个案例,每个案例由两行组成:上方为上颌牙齿,下方为下颌牙齿。红色框标记区域( )表示相邻牙齿间存在碰撞或间隙过大问题的情况,蓝色框标记区域( )表示牙齿朝向不当的情况,绿色框标记区域( )表示牙齿位置异常导致牙弓不规则的情况。

Fig. 7. Visualization results on the external dataset (Wang et al., 2024) compared with other methods. Here, three cases are shown and each case is represented by two rows:the upper teeth above and the lower teeth below. The meanings of color-coded boxed regions are consistent with those defined in Fig. 6.
图7 外部数据集(Wang等,2024)上与其他方法的对比可视化结果。此处展示了三个案例,每个案例由两行组成:上方为上颌牙齿,下方为下颌牙齿。彩色框标记区域的含义与图6中的定义一致。
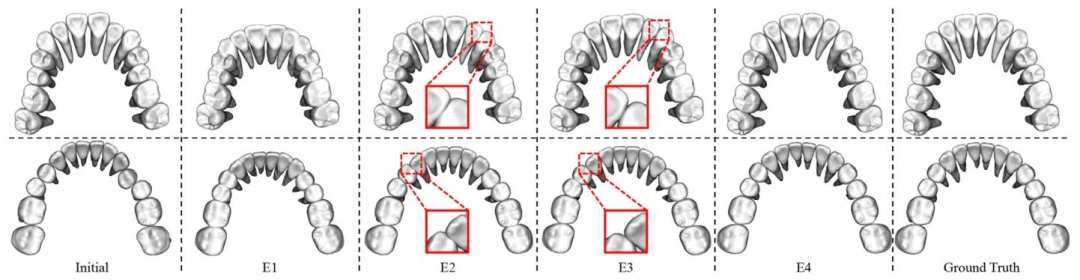
Fig. 8. Visualization of our ablation study of the hierarchical constraints in our CLIK-Diffusion. The upper row represents the upper teeth and the lower row represents the lowerteeth. E1 to E4 are four experiments consistent with Table 3, denoting the hierarchical constraints are progressively incorporated into the diffusion model.
图8 我们的CLIK-Diffusion中层级化约束消融研究的可视化结果。上行为上颌牙齿,下行为下颌牙齿。E1至E4为与表3一致的四个实验,代表层级化约束被逐步整合到扩散模型中的过程。
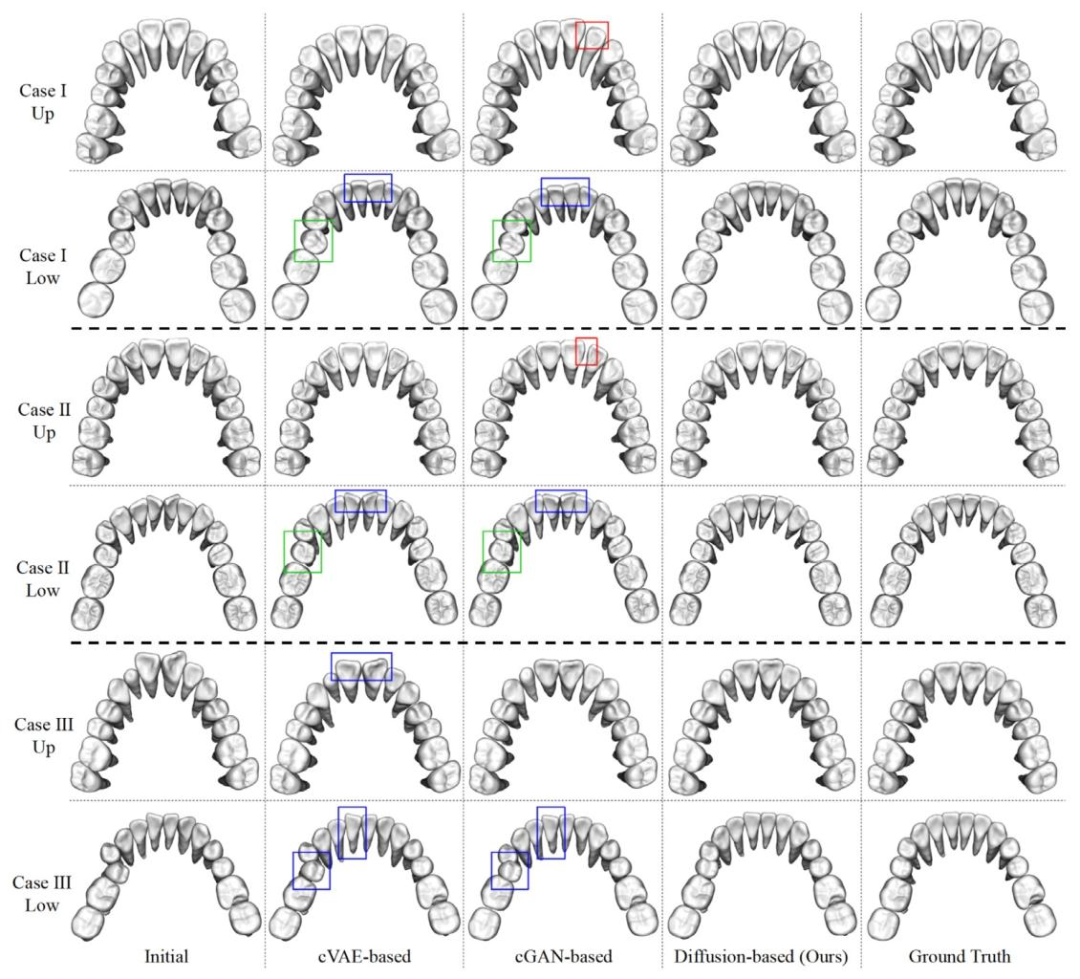
Fig. 9. Visualization results compared with cVAE-based and cGAN-based backbones. Here, three cases are shown and each case is represented by two rows: the upper teeth aboveand the lower teeth below. The first two cases correspond to the same patients shown in the first two cases of Fig. 6. The meanings of color-coded boxed regions are consistentwith those defined in Fig. 6.
图9 与基于条件变分自编码器(cVAE)和条件生成对抗网络(cGAN)的骨干模型对比的可视化结果。此处展示了三个案例,每个案例由两行组成:上方为上颌牙齿,下方为下颌牙齿。前两个案例与图6中的前两个案例对应同一患者。彩色框标记区域的含义与图6中的定义一致。
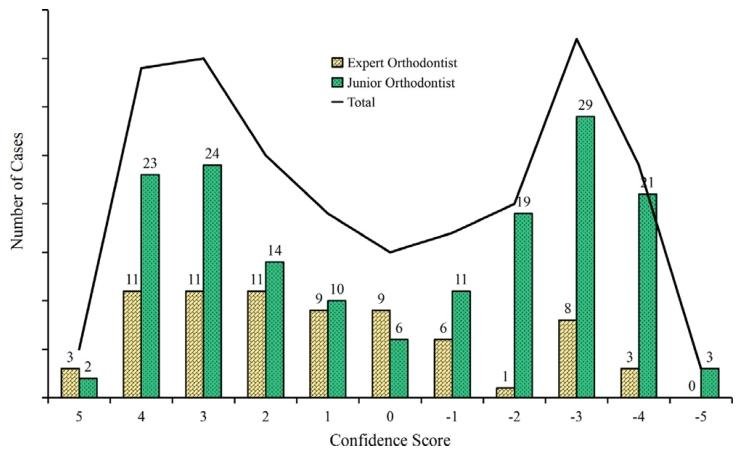
Fig. 10. Distribution of confidence scores for identifying the ground truth dentition.The yellow bars represent the confidence scores assigned by expert orthodontists, whilethe green bars correspond to those from junior orthodontists. The black line indicatesthe total number of cases for each confidence score. Positive scores reflect correctidentification, with higher values indicating greater certainty, while negative scoresreflect incorrect identification.
图10 识别真实牙列的置信度评分分布。黄色柱形代表正畸专家给出的置信度评分,绿色柱形代表初级正畸医生给出的置信度评分。黑色线条表示每个置信度评分对应的案例总数。正评分反映正确识别,分值越高表示确定性越强;负评分反映错误识别。
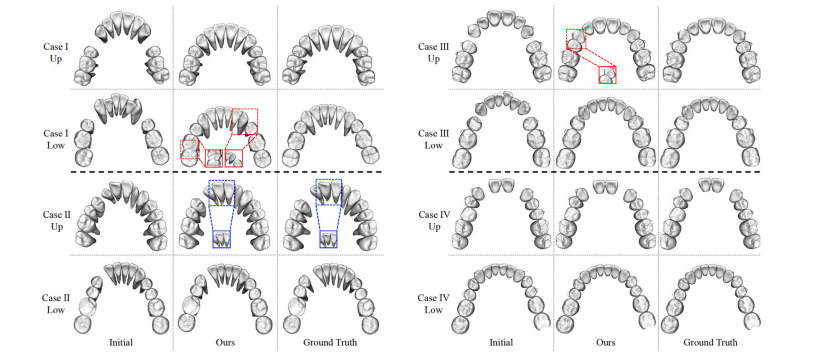
Fig. 11. Visualization results of cases with missing teeth. Here we show four test cases, two of which (Cases I and II) are from our own dataset and the other two (Cases III andIV) are from the external dataset (Wang et al., 2024). Each case is represented by two rows: the upper teeth above and the lower teeth below. The red-boxed zoom-in regionindicates the contact relationship between neighboring teeth, while the blue-boxed zoom-in region shows the orientation of the teeth
图11 牙齿缺失病例的可视化结果。此处展示了四个测试案例,其中两个(案例I和II)来自我们自己的数据集,另外两个(案例III和IV)来自外部数据集(Wang等,2024)。每个案例由两行组成:上方为上颌牙齿,下方为下颌牙齿。红色框放大区域显示相邻牙齿间的接触关系,蓝色框放大区域显示牙齿的朝向。
Table
表

Table 1Quantitative results of comparative experiments with the other methods. The unit is millimeter (mm) except for 𝛥𝑅𝑜𝑡𝑎𝑡𝑖𝑜𝑛, which is in degree( ◦ ). The best metrics are shown in bold, and the symbol denotes p-values less than 0.01 as determined by a paired t-test when comparedto ours.
表1 与其他方法的对比实验定量结果。除𝛥𝑅𝑜𝑡𝑎𝑡𝑖𝑜𝑛(旋转差异)的单位为度(°)外,其余指标单位均为毫米(mm)。最佳指标以粗体**显示,符号\(\ast\)表示通过配对t检验与我们的方法对比时,p值小于0.01。

Table 2Quantitative results on the external dataset (Wang et al., 2024) compared with other methods. The unit is millimeter (mm) except for 𝛥**𝑅𝑜𝑡𝑎𝑡𝑖𝑜𝑛,which is in degree ( ◦ ). The best metrics are shown in bold, and the symbol denotes p-values less than 0.01 as determined by a paired t-testwhen compared to ours.
表2 外部数据集(Wang等,2024)上与其他方法的对比定量结果。除𝛥𝑅𝑜𝑡𝑎𝑡𝑖𝑜𝑛(旋转差异)的单位为度(°)外,其余指标单位均为毫米(mm)。最佳指标以粗体显示,符号(\ast)表示通过配对t检验与我们的方法对比时,p值小于0.01。

Table 3Ablation study of the hierarchical knowledge-informed constraints in our CLIK-Diffusion. The unit is millimeter (mm) except for 𝛥𝑅𝑜𝑡𝑎𝑡𝑖𝑜𝑛, whichis in degree ( ◦ ). The best metrics are shown in **bold**, and the symbols and denote p-values less than 0.05 and 0.01, respectively, asdetermined by a paired t-test when compared to the preceding experimental condition.
表 3 我们的 CLIK-Diffusion 中层级化知识感知约束的消融研究结果。除𝛥𝑅𝑜𝑡𝑎𝑡𝑖𝑜𝑛(旋转差异)的单位为度(°)外,其余指标单位均为毫米(mm)。最佳指标以粗体显示,符号和分别表示通过配对 t 检验与前一实验条件对比时,p 值小于 0.05 和 0.01。

Table 4Ablation study of the dentition descriptor technique. The unit and symbols , are consistent with Table 3
表4 牙列描述符技术的消融研究结果。单位及符号(*)、(\ast\ast)的含义与表3一致。

Table 5Quantitative results compared with cVAE-based and cGAN-based backbones. The unit is millimeter (mm) except for 𝛥𝑅𝑜𝑡𝑎𝑡𝑖𝑜𝑛, which is in degree( ◦ ). The best metrics are shown in bold, and the symbols and denote p-values less than 0.05 and 0.01, respectively, as determined by apaired t-test when compared to ours.
表5 与基于条件变分自编码器(cVAE)和条件生成对抗网络(cGAN)的骨干模型对比的定量结果。除𝛥𝑅𝑜𝑡𝑎𝑡𝑖𝑜𝑛(旋转差异)的单位为度(°)外,其余指标单位均为毫米(mm)。最佳指标以粗体显示,符号(*)和(\ast\ast)分别表示通过配对t检验与我们的方法对比时,p值小于0.05和0.01。

Table 6Results of our user study on alignment scores. We calculate the average alignment scores graded by all participants for all cases, along withthe corresponding standard deviations.
表6 我们关于矫正评分的用户研究结果。表中计算了所有参与者对所有案例的平均矫正评分及相应的标准差。