P. S.：以下代码均在VS2019环境下测试，不代表所有编译器均可通过。 P. S.：测试代码均未展示头文件stdio.h的声明，使用时请自行添加。
目录
1、计数排序的基本思想
计数排序又称为鸽巢原理，是对哈希直接定址法的变形应用。
操作步骤：
- 统计相同元素出现次数
- 根据统计的结果将序列回收到原来的序列中
2、计数排序的思想过程
现有示例数组，成员为2，5，3，0，2，3，0，3。
通过直接观察我们可知数组中A最大元素为5，最小为0，故我们直接另开辟一个大小为六个整形的数组B，并通过calloc直接对数组B进行初始化为0。
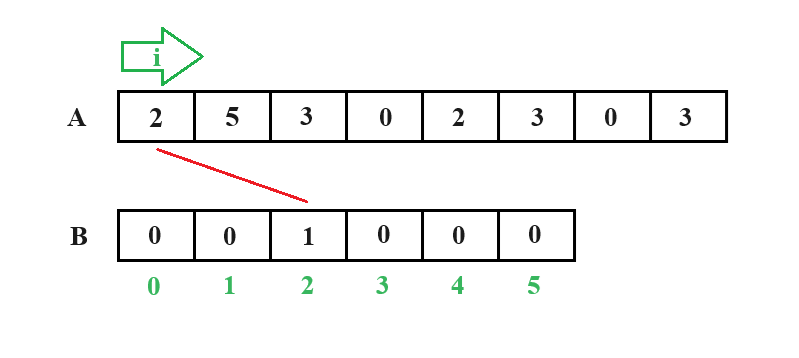
而后使用变量 i 对数组A进行遍历，然后让数组B中下标为A i 位置的数值加一，及如上所示。
而后继续遍历，直到遍历到数组A结束，如下所示。
在遍历结束后，数组B中所存数值为其下标数字在数组A中出现的次数，因为下标顺序本就是有序，故可直接按照其下标顺序进行对数组A的数值覆盖，当遇到下标所在位置为0时直接略过，即如下所示：
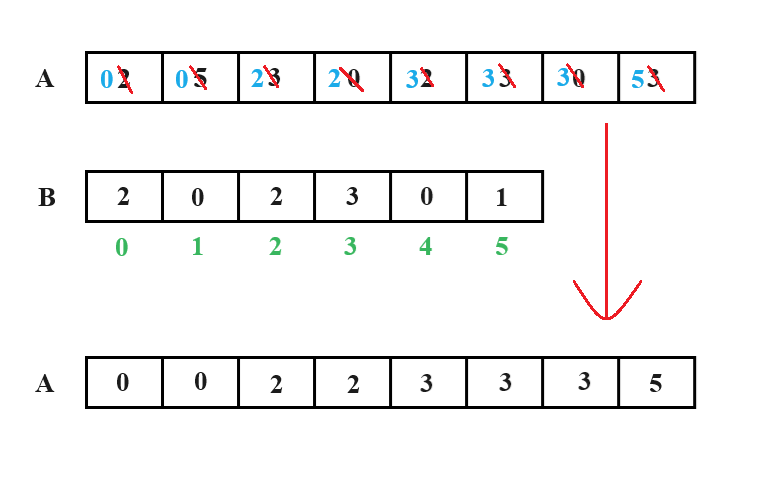此时数组A就是在原数组基础上的有序数组了，记得释放动态开辟出的空间数组B哦。
3、计数排序的优化
上文中展示了有限数组的计数排序方法，那如果所给数组个数未知，且数组元素差值远远小于所给数组元素的个数（例如10000个元素的数组中，最大值为9999，最小值为9990），那我们所开辟的动态数组就可不必开辟10000个整型变量的大小，只需开辟（最大值 - 最小值 + 1 ）个整型变量大小即可，因为其中的元素不同的个数仅有10个。
4、优化后的计数排序完整代码展示
完整代码如下所示
c
#include <stdio.h>
#include <stdlib.h>
void CountSort(int* a, int n)
{
int max = a[0];
int min = a[0];
for (int i = 0; i < n; i++)
{
if (max < a[i])
max = a[i];
if (min > a[i])
min = a[i];
}
int range = max - min + 1;
int* tmp = (int*)calloc(range, sizeof(int));
if (tmp == NULL)
{
perror("CountSort: calloc fail");
return;
}
for (int i = 0; i < n; i++)
{
tmp[a[i] - min]++;
}
int j = 0;
for (int i = 0; i < range; i++)
{
while(tmp[i]--)
{
a[j++] = i + min;
}
}
free(tmp);
}
void test01()
{
int a[] = { 3,4,3,6,4,5,6,1,3,2,7,8,7,9,5 };
int n = sizeof(a) / sizeof(a[0]);
CountSort(a, n);
for (int i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
printf("\n");
}
int main()
{
test01();
return 0;
}5、结语
十分感谢您观看我的原创文章。
本文主要用于个人学习和知识分享，学习路漫漫，如有错误，感谢指正。
如需引用，注明地址。