规律一致性分析的实际作用
在实际建模过程中,规律一致性分析是非常重要但又经常容易被忽视的一个环节。通过规律一致性分析,我们可以得出非常多的可用于后续指导后续建模的关键性意见。通常我们可以根据规律一致性分析得出以下基本结论:
(1).如果分布非常一致,则说明所有特征均取自同一整体,训练集和测试集规律拥有较高一致性,模型效果上限较高,建模过程中应该更加依靠特征工程方法和模型建模技巧提高最终预测效果;
(2).如果分布不太一致,则说明训练集和测试集规律不太一致,此时模型预测效果上限会受此影响而被限制,并且模型大概率容易过拟合,在实际建模过程中可以多考虑使用交叉验证等方式防止过拟合,并且需要注重除了通用特征工程和建模方法外的trick的使用;
4.规律一致性分析
接下来,进行训练集和测试集的规律一致性分析。
所谓规律一致性,指的是需要对训练集和测试集特征数据的分布进行简单比对,以"确定"两组数据是否诞生于同一个总体,即两组数据是否都遵循着背后总体的规律,即两组数据是否存在着规律一致性。
我们知道,尽管机器学习并不强调样本-总体的概念,但在训练集上挖掘到的规律要在测试集上起到预测效果,就必须要求这两部分数据受到相同规律的影响。一般来说,对于标签未知的测试集,我们可以通过特征的分布规律来判断两组数据是否取自同一总体。
单变量分析
首先我们先进行简单的单变量分布规律的对比。由于数据集中四个变量都是离散型变量,因此其分布规律我们可以通过相对占比分布(某种意义上来说也就是概率分布)来进行比较。
例如首先我们查看首次激活月份的相对占比分布可以通过如下代码实现:
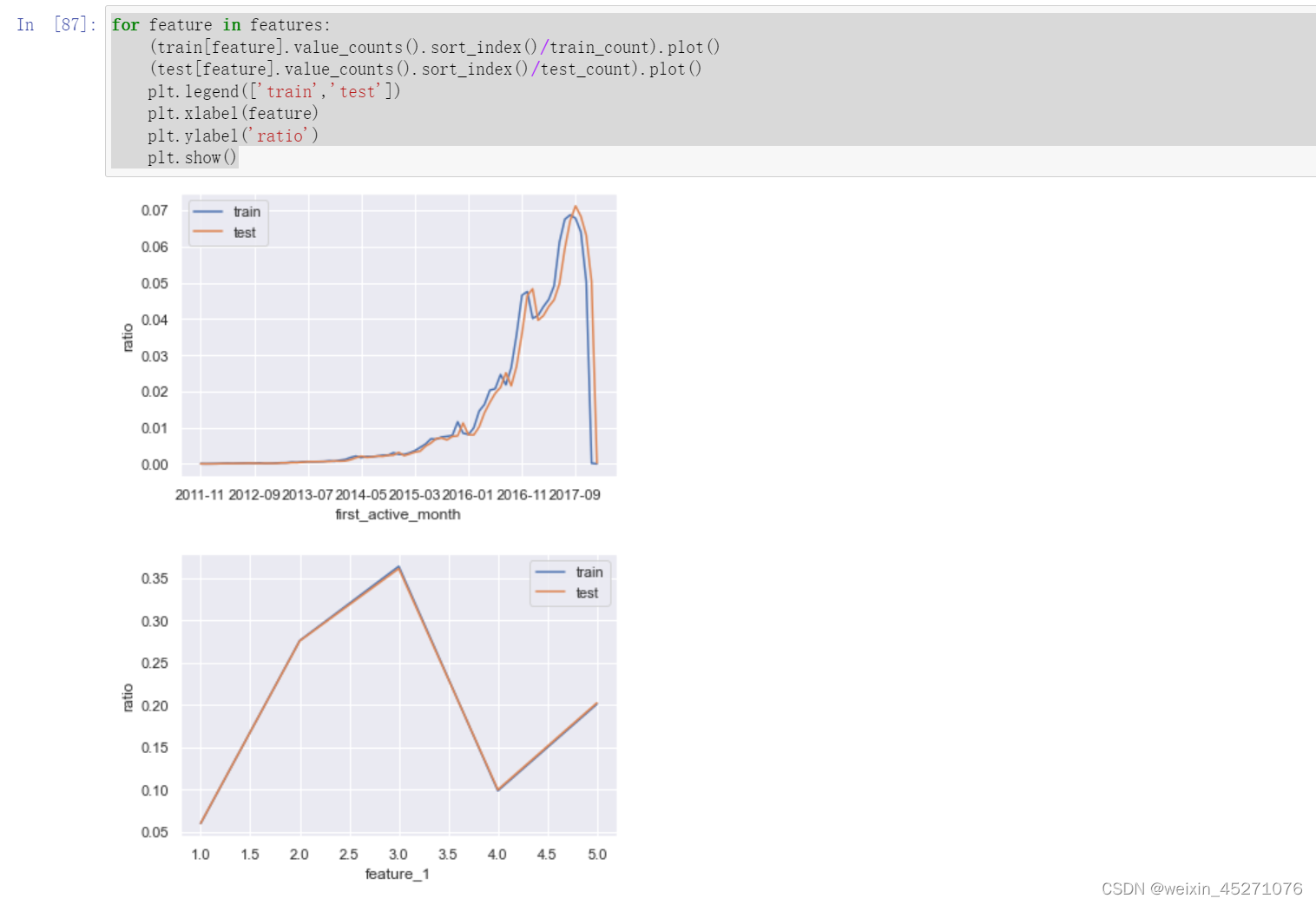
能够发现,两组数据的单变量分布基本一致。
多变量联合分布
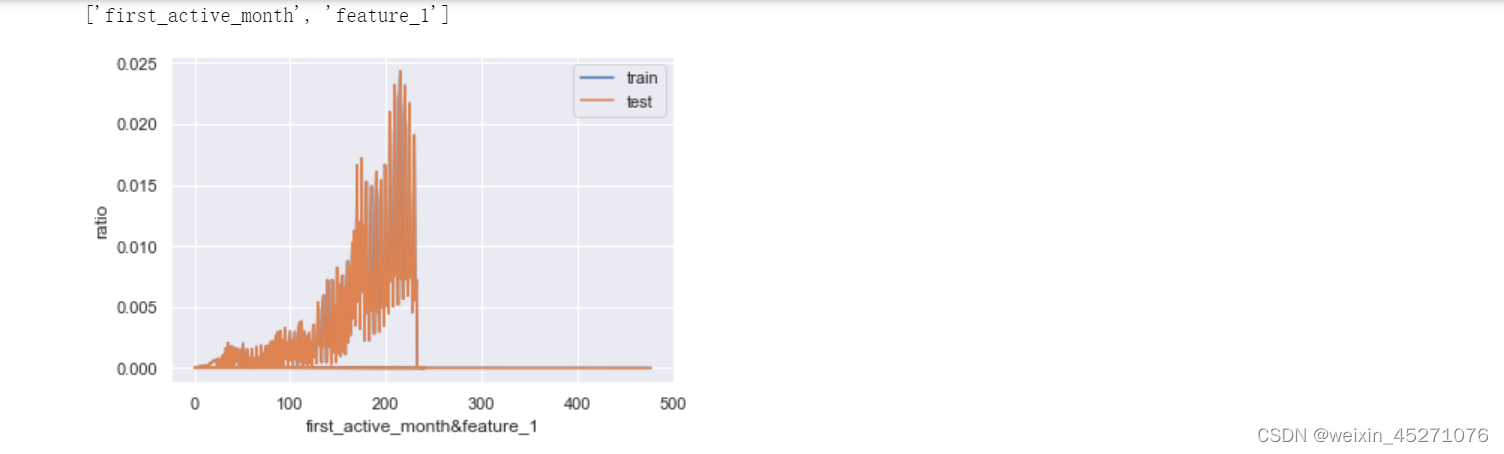
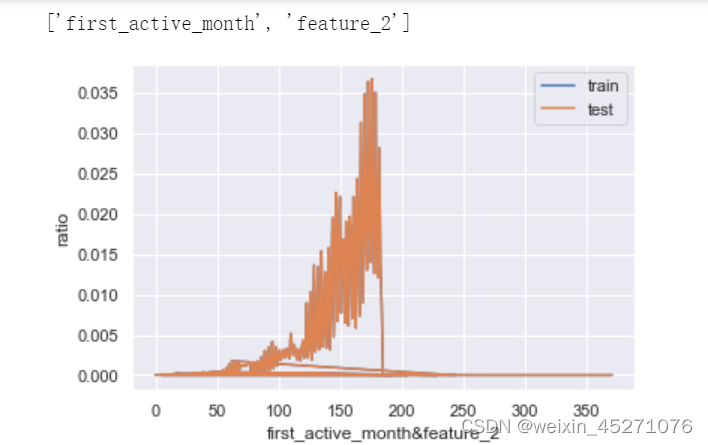
接下来,我们进一步查看联合变量分布。所谓联合概率分布,指的是将离散变量两两组合,然后查看这个新变量的相对占比分布。例如特征1有0/1两个取值水平,特征2有A/B两个取值水平,则联合分布中就将存在0A、0B、1A、1B四种不同取值水平,然后进一步查看这四种不同取值水平出现的分布情况。
首先我们可以创建如下函数以实现两个变量"联合"的目的:
c
n = len(features)
for i in range(n-1):
for j in range(i+1, n):
cols = [features[i], features[j]]
print(cols)
train_dis = combine_feature(train[cols]).value_counts().sort_index()/train_count
test_dis = combine_feature(test[cols]).value_counts().sort_index()/test_count
index_dis = pd.Series(train_dis.index.tolist() + test_dis.index.tolist()).drop_duplicates().sort_values()
(index_dis.map(train_dis).fillna(0)).plot()
(index_dis.map(train_dis).fillna(0)).plot()
plt.legend(['train','test'])
plt.xlabel('&'.join(cols))
plt.ylabel('ratio')
plt.show()在这里插入图片描述