力扣40. 组合总和 II

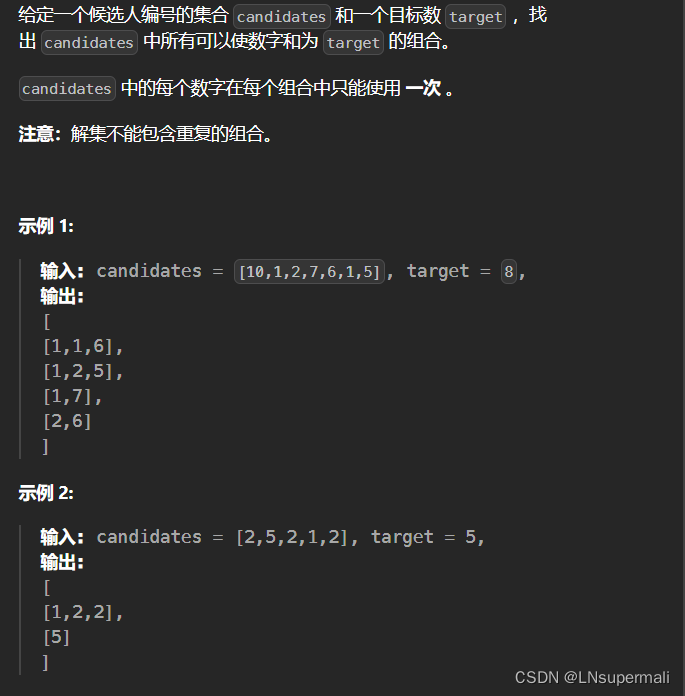
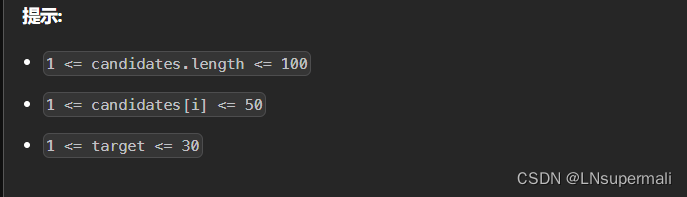
Problem: 40. 组合总和 II

文章目录

题目描述
思路及解法
复杂度
Code

题目描述

思路及解法

1.创建一个 res 变量存储所有满足条件的组合结果，使用 track 变量记录当前的组合路径，使用 trackSum 变量记录当前路径中元素的和。

2.排序: 对 candidates 数组进行排序，使得相同的元素聚集在一起，便于后续去重处理。
3.回溯方法 backtrack：

3.1.基本情况1：如果 trackSum 等于目标 target，则将当前路径 track 添加到结果 res 中，并返回。

3.2.基本情况2：如果 trackSum 大于目标 target，则直接返回。
4.循环与选择：
4.1.循环从 start 位置开始遍历 nums 数组。

4.2.如果当前元素与前一个元素相同，跳过本次循环，避免重复计算。

4.3.将当前元素添加到 track 中，并更新 trackSum。

4.4.递归调用 backtrack 方法，并将 start 位置更新为 i + 1，继续处理后续元素。

4.5.回溯：从 track 中移除最后一个元素，并更新 trackSum，以便尝试其他组合。

复杂度

时间复杂度:

O ( 2 n ) O(2^n) O(2n);其中 n n n为给定数组nums的大小

空间复杂度:

O ( 2 n × n ) O(2^n \times n) O(2n×n)

Code

java 复制代码

class Solution {
    List<List<Integer>> res = new LinkedList<>();
    // Record the backtracking path
    LinkedList<Integer> track = new LinkedList<>();
    // Record the sum of elements in the track
    int trackSum = 0;

    /**
     * Combination Sum II
     *
     * @param candidates Specific list
     * @param target     target
     * @return List<List < Integer>>
     */
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        if (candidates.length == 0) {
            return res;
        }
        // Sort first so that the same elements are close together
        Arrays.sort(candidates);
        backtrack(candidates, 0, target);
        return res;
    }

    /**
     * Solve for all subsets of specified values using backtracking
     *
     * @param nums   Given array
     * @param start  Decision stage
     * @param target target
     */
    private void backtrack(int[] nums, int start, int target) {
        // base case, reach the target and find the combination that
        // meets the conditions
        if (trackSum == target) {
            res.add(new LinkedList<>(track));
            return;
        }
        // base case, exceed target sum, end directly
        if (trackSum > target) {
            return;
        }
        for (int i = start; i < nums.length; ++i) {
            if (i > start && nums[i] == nums[i - 1]) {
                continue;
            }
            track.add(nums[i]);
             trackSum += nums[i];
            backtrack(nums, i + 1, target);
            track.removeLast();
            trackSum -= nums[i];
        }
    }
}