cpp
复制代码
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <assert.h>
#define MAX 100
#define NO 0xFFFFFF
typedef struct Graph
{
int arcnum;
int vexnum;
char vextex[MAX][20];
int matrix[MAX][MAX];
}Graph;
void print_graph(Graph* g)
{
for (int i = 0; i < g->vexnum; i++)
{
printf("\t%s", g->vextex[i]);
}
printf("\n");
for (int i = 0; i < g->vexnum; i++)
{
printf("%s\t", g->vextex[i]);
for (int j = 0; j < g->vexnum; j++)
{
if (g->matrix[i][j] == NO)
{
printf("NO\t");
}
else
{
printf("%d\t", g->matrix[i][j]);
}
}
printf("\n");
}
}
//狄克斯特拉算法
void graph_dijkstra(Graph* g, int in, int dist[])
//in为起始要求的到其他点最短路径的点,dist数组用于记录到该点的距离(如果有更短的则在上面更新)
{
int flag[MAX];//成功获取路径的标记
int path[MAX];//记录每个节点的前驱节点
for (int i = 0; i < g->vexnum; i++)
{
flag[i] = 0; //将所有顶点都置为未访问
dist[i] = g->matrix[in][i]; //获取起始顶点到其它所有顶点的权值
path[i] = in; //先将所有结点的前驱结点都设为初始的in顶点
}
flag[in] = 1; //起始节点置为已访问
dist[in] = 0; //起始顶点自己到自己的距离为0
int min;
int j;//用于控制循环
int k;//用于记录边权值最小终点的下标
for (int i = 1; i < g->vexnum; i++)
{
//找最小的
min = NO;
for (j = 1; j < g->vexnum; j++)//注意j要从1开始,因为起始点下标为0
{
//当该节点未被访问(或者说该边权值未被加入到最短路径中)且该点对应边权值已被加入到dist数组中去
if (flag[j] == 0 && dist[j] < min)
{
min = dist[j]; //先找到与邻接点最小的权值并记录,且记录该结点
k = j;
}
//最终找到最小的
}
//加上原路径 小于直接路径 更新
flag[k] = 1; //将找到的邻接边权值最小的终点置为已访问
for (j = 1; j < g->vexnum; j++)
{
if (flag[j] == 0 && min + g->matrix[k][j] < dist[j])
{
//如果该结点没被访问且加上原路径小于直接路径则更新,将边权值加入到数组dist中
//这个操作相当于开辟边,让下一次的循环是一个有边的状态,可用于比对然后加入将最短权值点置为已访问
dist[j] = min + g->matrix[k][j];
path[j] = k; //将其前驱节点置为k
}
}
}
//使用数据结构栈来打印最短路径
for (int i = 1; i < g->vexnum; i++)
{
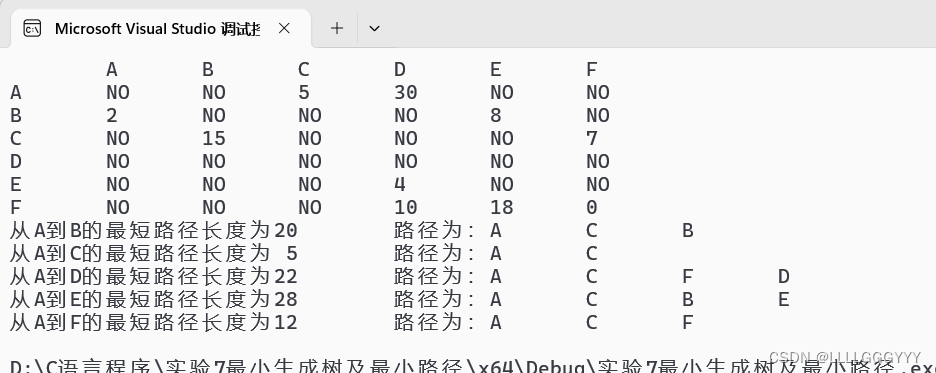
printf("从%s到%s的最短路径长度为%2d\t",g->vextex[in],g->vextex[i],dist[i]);
//输出路径
printf("路径为:%s\t",g->vextex[in]);
char stack[MAX][20];
int top = -1;
int prev = path[i];//prev是该终点的前驱节点
while (prev != in)
{
strcpy_s(stack[++top], 20, g->vextex[prev]);
prev = path[prev];
}
while (top != -1)
{
printf("%s\t",stack[top--]);
}
printf("%s\n",g->vextex[i]);//最后再将终点输出来
}
}
int main(int argc, char* argv[])
{
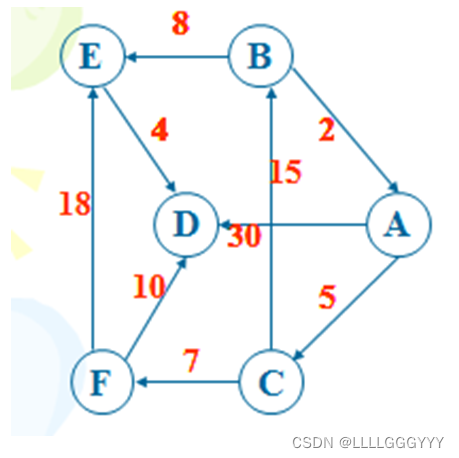
Graph g =
{ 9,6,{"A","B","C","D","E","F"},
{
{NO,NO,5,30,NO,NO},
{2,NO,NO,NO,8,NO},
{NO,15,NO,NO,NO,7},
{NO,NO,NO,NO,NO,NO},
{NO,NO,NO,4,NO,NO},
{NO,NO,NO,10,18}
}
};
print_graph(&g);
int in = 0;
int dist[MAX] = { 0 };
graph_dijkstra(&g, in, dist);
return 0;
}