文章目录
- [0. 概述](#0. 概述)
- [1. BAG](#1. BAG)
- [2. ADT](#2. ADT)
0. 概述
学习下优先级搜索
1. BAG

优先级搜索是非常广义的,概况来说,无论DFS 还是BFS从逻辑上来都属于这种搜索。
回忆下什么叫搜索或者遍历,对于像图这种数据结构里的元素逐一的没有重复的也没有遗漏的对它们进行访问,在不同的应用问题里,这种访问其实最最重要的是次序,怎么确定次序?
~以前在初级的数据结构,比如向量或者列表为代表,那种次序取决于结构本身的,它的结构是线性的,从头到尾从左到右一个一个访问过去就可以,线性在数学里是有很多含义在里面,既可以认为它有这种前驱后继,线性还有一些意思------是否显示的可以预测的。
~很多问题经常可以听到这是个非线性问题,什么叫非线性问题,说穿了就是在处理这个问题的时候,几乎只能用一种边走边看的策略,不可能一眼看穿,虽然心里知道在数学上肯定是确定的,但是它不会那么显示的更不会那么简明的给出这个次序,所以大概是一种摸着石头过河,慢慢地,走一步算一步。在这样一种非线性情况下,更重要的是通过一种策略来确定一种次序,比如可行的一种策略是:遍历到第k步,已经有k个元素被访问过了,那么第k+1个是谁?如果有一种策略,根据彼时彼刻地场景,能够确定下一个是谁,那不就可以了嘛。
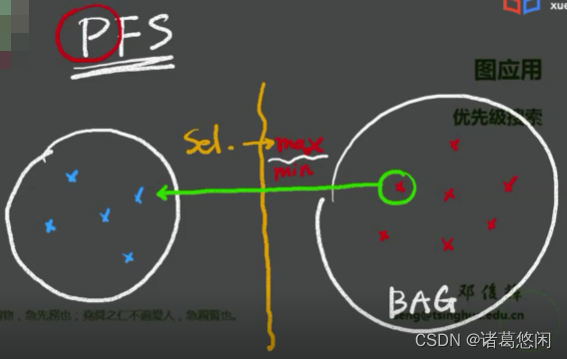
优先级搜索PFS中重要的当然是优先级,它大概来说是借用某一种数据结构来处理这种东西的,这种数据结构笼统叫做BAG。
就像书包一样,所有的元素(红色的)一开始都在包里面,接下来会有一个访问完了的容器,它们中间会有一根线,这个线很重要,表示是访问完了的还是没有访问的,假设已经有部分元素访问完了(蓝色的),那么现在最核心的问题就是接下来要挑谁?
~这个所谓的第k+1个到底是谁,如果能够确定,对它进行访问并把它挪过来。如果有这个简明的策略,可以持续的反复的不断的进行操作,这不就是一个遍历的算法嘛。
~实际上,所有的东西从这个方向来审视都可以化为一个复杂的那样过程,但是每次都是一个很简明的策略,它其实都是去解释BAG中所有的元素各自的优先级。这个策略变得这么简单了,于是这个问题就转化为最最重要的BAG是什么,其实不同的BAG就会导致不同的优先级分配,当然也包括选取。
概括下所谓的PFS就是用某种数据结构把这些元素组织起来并且每个元素分配一个优先级,接下来过程每次都是做一个selection,选出来并标记为visited,接下来repeat,知道BAG耗尽。
2. ADT

对一个图的pfs,方法也是从任何一个点开始,通过迭代或递归做下去,这个过程是非线性,非线性允许这些元素的priority会有所变化,所以必然有更新priority的过程,这里把更新优先级的过程使用函数对象写出来,首先初始化s状态值,while中每次都找出最高优先级元素,把它摘出来并作访问。
while怎么作?

前面两行就是update priority。
每个元素优先级如果有改变的话,只有一个机会,当有一个元素这里取s被选出并访问,有些节点会占它的光,有机会提升它的优先级,这些节点就是它的邻居。对它的每一个相邻元素这里取w取出来,更新器priUpdater策略------(this)依据当前这幅图,如果确认s刚刚被访问过,它的邻居w便有机会update,具体的update依据算法而异。
update后,接下来select 出最高优先级元素
for循环虽然看起来复杂但活做的简单,就是从一个预设的开始,对于所有UNDISCOVERED的点(BAG中的元素)进行比较并更新优先级并记下对象。
选出来后,将这个点加入到已选的BAG中
这里借助函数对象prioUpdater,使算法设计者得以根据不同的问题需求,简明地描述和实现对应的更新策略。具体地,只需重新定义prioUpdater对象即可,而不必重复实现公共部分。比如,此前的BFS搜索和DFS搜索都可按照此模式统一实现。
后面,以最小支撑树和最短路径这两个经典的图算法为例,深入介绍这一框架的具体应用。
- 复杂度
