最近在学习机器人的仿真,仿真平台基于simscape。
简介
simscape是matlab一个仿真利器,在simulink中点击库浏览器按键翻阅即可找到
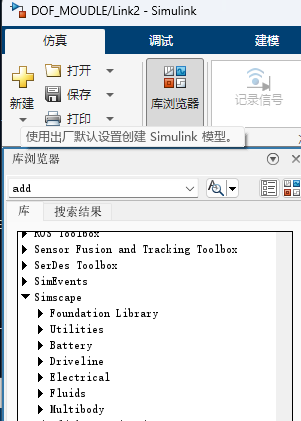
通过上图可以发现simscape的研究领域众多有电池 自动驾驶 电力 流体 刚体等领域,对于机器人领域(不排除特殊机器人)需要一般的是mutibody这一栏的基本元素。
模型建模
模型建模一共分为两部分:搭地基和盖楼
搭地基
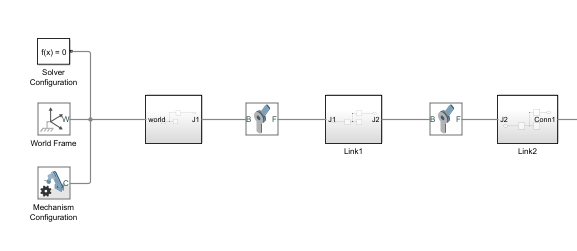
打搭建地基共需要三个元素:1.Solver configuration 2.world frame 3.mechanism configuration
首先 solver(求解器) configuration 确定世界的计算规则
其次 world Frame 确定世界坐标(学习机器人运动学可知)
最后是 Mechanism configuration 确定世界基本物理定律(重力等等)
盖楼
盖楼一共分为4部分:坐标变化 刚体 连接间 限制元素
坐标变化
坐标变化一般用的是rigid transform元素,其中主要有旋转和平移的选择
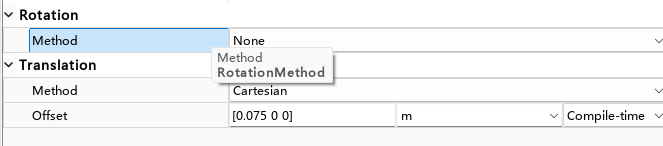
旋转和平移的众多参数如下:
旋转:
需要注意的是旋转的方向是逆时针为正
| 方法 | 核心思路 | 适用场景与输入方式 |
|---|---|---|
| None | 不进行旋转对齐。两个坐标系的坐标轴方向完全一致。 | 默认选项。当两个部件连接时,它们的局部坐标系轴向本来就已对齐,无需额外旋转。 |
| Aligned Axes | 轴对齐。通过指定"哪个轴(X/Y/Z)对齐到哪个目标轴"来定义旋转,相当于坐标轴映射。 | 最符合直觉的方法之一。例如,定义"将零件A的Z轴,对齐到零件B的X轴的方向"。 |
| Standard Axis | 标准轴旋转 。绕着一个指定坐标轴(X/Y/Z) 旋转一个角度。 | 最常用、最直观的方法。例如,让一个零件"绕其自身的Z轴旋转90度"。与位置偏移中的"Standard Axis"思路一致。 |
| Arbitrary Axis | 绕任意轴旋转 。定义一个三维空间中的向量轴 ,并绕此轴旋转一个角度。 | 当旋转轴不恰好是X、Y、Z坐标轴时使用。例如,绕一个斜着的轴(如[1, 1, 0]方向)旋转。 |
| Rotation Sequence | 旋转序列 (欧拉角)。通过按特定顺序绕不同轴连续旋转三次来定义最终姿态。 | 描述复杂姿态的标准方法。需选择顺序(如Z-Y-X)并输入三个角度。这是航空航天领域(俯仰、偏航、滚转)的数学基础。 |
| Rotation Matrix | 旋转矩阵。直接输入一个3x3的旋转矩阵。 | 底层数学表示。当您直接从其他计算或软件中得到了旋转矩阵时使用。最不直观,但数学上最完备。 |
| Quaternion | 四元数。输入一个四维向量 [w, x, y, z] 来描述旋转。 | 用于高级控制、插值或避免"万向节死锁"。在复杂连续旋转(如机器人、动画)中计算效率高且无奇点。 |
平移:
| 方法名称 | 核心思路 | 适用场景与输入方式 |
|---|---|---|
| **Cartesian (笛卡尔坐标)** | 最直观。通过直接指定在X、Y、Z三个坐标轴方向上的偏移量来定义平移。 | 通用场景 。绝大多数常规的位置摆放。例如,直接输入偏移量 [0.1, 0.05, 0.02]米,表示在X、Y、Z方向分别移动相应的距离。 |
| **Standard Axis (标准轴)** | 最智能 。沿着参考对象自身的某一个坐标轴移动指定的距离。 | 零件需要沿主轴线安装的情况。例如,将一个连杆的末端沿着它自身的长度方向(通常是其Z轴)移动一段距离。输入时,需选择一个轴(X/Y/Z)并指定一个距离值。 |
| **Cylindrical (柱面坐标)** | 最方便 。使用半径、角度、高度三个参数来描述点在空间中的位置,非常适合圆周或径向布局。 | 零件以圆周阵列、旋转对称或沿径向分布的情况。例如,在法兰盘上打一圈孔。输入参数为半径、角度和Z轴高度,避免了手动计算直角坐标的麻烦。 |
刚体
在刚体选择中有众多元素,但是我们常用 cylindrical 和 brick,其他元素如下面的表格列出
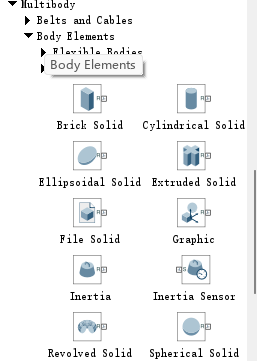
| 模块名称 | 核心功能 | 典型建模场景 |
|---|---|---|
| Brick Solid (长方体刚体) | 创建一个具有长方形六面体几何形状的刚体。 | 机座、平台、滑块、箱子等任何具有规则立方体形状的部件。 |
| Cylindrical Solid (圆柱体刚体) | 创建一个圆柱体形状的刚体。 | 轴、连杆、辊子、圆柱形支柱等旋转对称的零件。 |
| Ellipsoidal Solid (椭球体刚体) | 创建一个椭球体(橄榄球状)形状的刚体。 | 特殊形状的配重、流线型物体或某些具有椭球外观的部件。 |
| Extruded Solid (拉伸体刚体) | 通过沿法向拉伸一个自定义的二维横截面来创建复杂棱柱体刚体。 | 具有复杂但恒定截面的型材,如工字梁、C型槽钢、齿轮齿廓、自定义框架等。 |
| File Solid (文件导入刚体) | 从外部CAD软件生成的STL等三维模型文件导入几何形状,以创建高精度的刚体。 | 当部件形状复杂,无法用基本几何体描述时使用。这是将专业CAD设计导入Simscape进行仿真的主要方式。 |
| Graphic (图形刚体) | 创建一个仅具有可视化几何外形,但没有质量、惯性等物理属性的"壳"。用于辅助显示。 | 创建不参与动力学计算的视觉参考物、外壳、装饰性部件,或用于标识空间位置。 |
| Inertia (惯性刚体) | 定义一个仅有质量属性(质量、惯性矩),但没有可视化几何形状的抽象刚体。 | 当您需要为一个复杂装配体定义集中质量参数,或进行简化动力学分析而无需关注具体形状时使用。 |
| Inertia Sensor (惯性传感器) | 在指定位置添加一个可测量该点加速度、角速度等惯性数据的传感器。 | 用于测量模型上特定点的运动状态,是动力学分析与控制系统设计的关键测量工具。 |
| Revolved Solid (旋转体刚体) | 通过绕一个轴旋转一个自定义的二维横截面来创建复杂旋转体刚体。 | 创建花瓶、瓶子、车轮、飞轮、轴对称零件等任何旋转对称的复杂几何体。 |
| Spherical Solid (球体刚体) | 创建一个球体形状的刚体。 | 滚珠、球铰链的球头、球形外壳、球形配重等。 |
连接件
连接件是连接刚体和刚体之间的物体,是物体运动的核心部件,我们在普通的使用场景应用revolte joint 和 weld joint(终点)
| 运动副名称 | 核心功能(允许的自由度) | 典型建模场景 |
|---|---|---|
| 6-DOF Joint (六自由度关节) | 允许所有6个相对运动自由度:3个平移(X, Y, Z)和3个旋转(绕X, Y, Z轴)。 | 用于创建完全自由的连接,如模拟太空中的卫星、飞机,或作为复杂机构的初始通用连接。 |
| Bushing Joint (衬套/弹性关节) | 在6个自由度上均提供线性刚度和阻尼,是一种柔性的、可发生弹性变形的连接。 | 模拟减震器、橡胶衬套、柔性安装座等,用于分析振动传递和柔性连接的影响。 |
| Constant Velocity Joint (等速万向节) | 允许在两个轴之间以恒定的转速比传递旋转,无论夹角如何。 | 模拟汽车驱动轴中的等速万向节(CV Joint),用于前轮驱动或独立悬架系统。 |
| Gimbal Joint (万向支架/虎克铰) | 允许绕两个相互垂直的轴旋转(2个旋转自由度),但不允绕第三个轴旋转。 | 模拟经典的万向节(Cardan/U-Joint),可用于方向传动,但注意其输出转速并不恒定。 |
| Pin Slot Joint (销槽关节) | 允许1个平移自由度和1个旋转自由度,但平移轴必须与旋转轴共面且垂直。 | 模拟曲柄滑块机构中,曲柄上的销钉在滑块的槽中运动。 |
| Prismatic Joint (移动轴/滑动关节) | 仅允许沿一个轴的平移运动(1个平移自由度)。 | 模拟液压缸、气缸、直线导轨、抽屉滑轨等直线运动。 |
| Revolute Joint (转动副/旋转关节) | 仅允许绕一个轴的旋转运动(1个旋转自由度)。 | 最常用的关节,模拟门铰链、车轮轴承、机器人关节、连杆机构中的旋转部分。 |
| Telescoping Joint (伸缩副) | 允许沿一个轴 的平移和绕同一个轴的旋转(1平移+1旋转,共2自由度)。 | 模拟可伸缩的天线、带有转动手柄的千斤顶、钻孔钻头等既伸缩又旋转的运动。 |
| Weld Joint (焊接关节) | 不允许任何相对运动(0自由度)。将两个刚体刚性固定在一起。 | 模拟焊接、铆接、螺栓紧固等永久性或刚性连接,将多个零件组合成一个整体部件。 |
| Spherical Joint (球铰副) | 允许绕所有三个轴的旋转(3个旋转自由度),但不允许任何平移。 | 模拟球窝接头,如汽车悬架中的球头销 、人体骨骼的髋关节或肩关节。 |
| Universal Joint (万向节) | 这是 Gimbal Joint 的另一个名称,功能完全相同。 | 同上。 |
限制元素
限制元素是限制物体运动的部件能够约束物体在安全范围运动
| 约束名称 | 核心功能 | 典型建模场景 |
|---|---|---|
| Angle Constraint (角度约束) | 强制规定两个刚体上的两条直线(或两个坐标系的一个轴)之间的夹角保持为设定值。 | 1. 保持两个部件(如太阳能电池板与支架)之间的相对角度固定。 2. 模拟一个可调但能锁定的角度(如台灯臂)。 |
| Distance Constraint (距离约束) | 强制规定两个刚体上的两个特定点之间的距离保持为设定值。 | 1. 模拟一根不可伸缩的刚性杆 或绳索,连接两个物体。 2. 保持两个旋转中心之间的固定距离(如曲柄连杆机构中的关键尺寸)。 |
| Point on Curve Constraint (曲线上的点约束) | 强制规定一个刚体上的一个特定点,必须始终位于另一个刚体所定义的一条曲线或边线上。 | 1. 模拟火车轮在轨道上行驶。 2. 模拟一个销钉在固定形状的凹槽中滑动(如凸轮机构的从动件)。 |
| Point on Surface Constraint (表面上的点约束) | 强制规定一个刚体上的一个特定点,必须始终位于另一个刚体所定义的一个曲面或平面上。 | 1. 模拟一个物体在复杂的曲面(如滑梯、山坡)上滑动。 2. 模拟棋盘上的棋子,被约束在棋盘平面内移动。 |
举一个例子
总的:
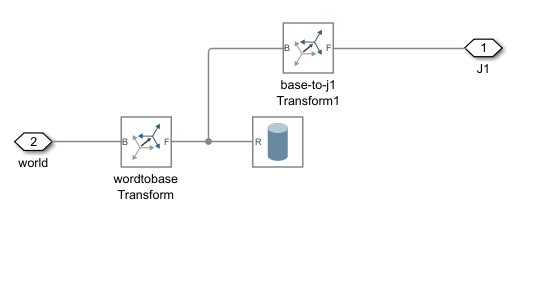
第一个子系统连接world和j1的
物体控制
实现对物体的控制在物理世界上,主要体现在关节的移动导致刚体的移动。在simulink中光说是关节的移动是不够的,我们还需要以下步骤:1 输入量的单位转化(sim to phy)2 连接件控制量和测量量等设置 3 输入信号设计 3.轨迹规划 4.机器人运动学动力学解算 5.控制器设计
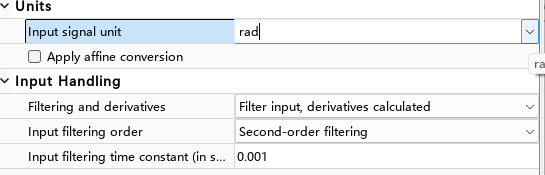
输入量的单位转化
需要注意以下单位:有角度 速度等等
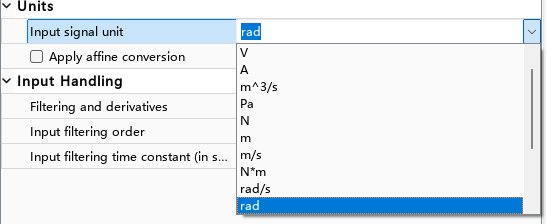
连接件控制量观测量等设置
连接件的配置主要位置运动限制 运动控制方式 和 观测量设置组成
具体配置如下
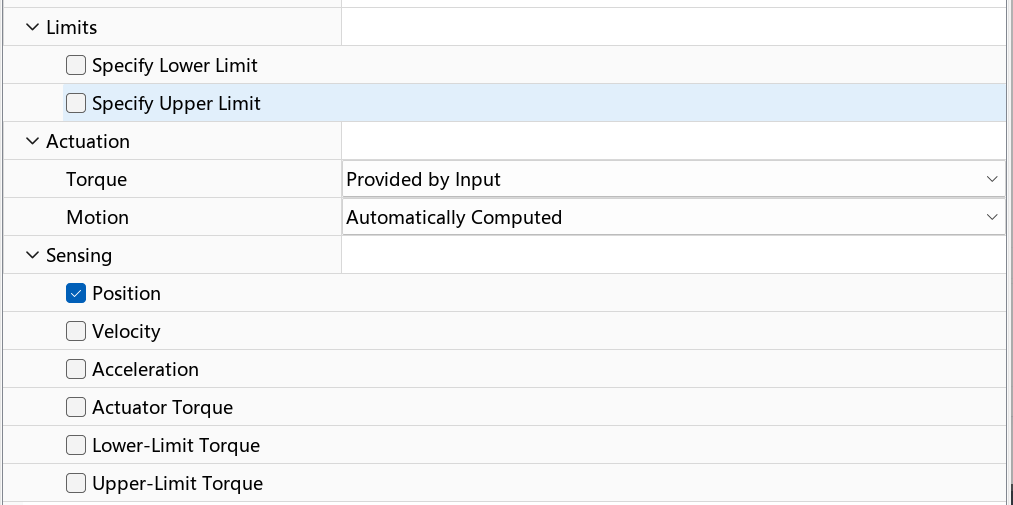
| 功能板块 | 参数名称 | 设置/选项 | 物理意义与作用 |
|---|---|---|---|
| **Limits (运动限制)** | Specify Lower Limit | 已勾选 | 启用下极限位置。 |
| - Bound (边界) | -90 deg |
关节旋转的下限位置为 -90 度。 | |
| - Spring Stiffness (弹簧刚度) | 1e4 N*m/deg |
当关节接近下限时,产生一个抵抗进一步运动的扭矩,刚度越大,反弹力越强。 | |
| - Damping Coefficient (阻尼系数) | 10 N*m/(deg/s) |
消耗接近下限时的能量,抑制振荡,使运动更平顺。 | |
| - Transition Region Width (过渡区宽度) | 0.1 deg |
在边界-90 deg的这0.1 deg范围内,弹簧和阻尼力从0平滑增加到全值,避免力的突变,保证仿真稳定。 |
|
| Specify Upper Limit | 已勾选 | 启用上极限位置。 | |
| - Bound (边界) | 90 deg |
关节旋转的上限位置为 90 度。 | |
| - 弹簧、阻尼、过渡区参数 | 同下限 | 作用同上限,方向相反。 | |
| **Actuation (驱动方式)** | **Torque (扭矩)** | Automatically Computed |
关节的扭矩由模型自动计算(例如,由重力、限制力、其他连接件相互作用得出),不额外施加驱动扭矩。 |
| **Motion (运动)** | Provided by Input |
关节的运动(位置、速度或加速度)将由外部输入信号指定。这是实现位置/速度/加速度控制的关键接口。 | |
| **Sensing (传感)** | **Position (位置)** | 已勾选 | 测量并输出 关节的**角度(或平移副的位移)** 物理信号。 |
输入信号与轨迹设计
通常使用signal editor
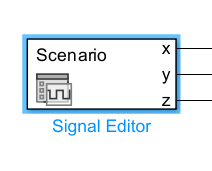
轨迹规划
对于机器人的轨迹规划有以下元素提供
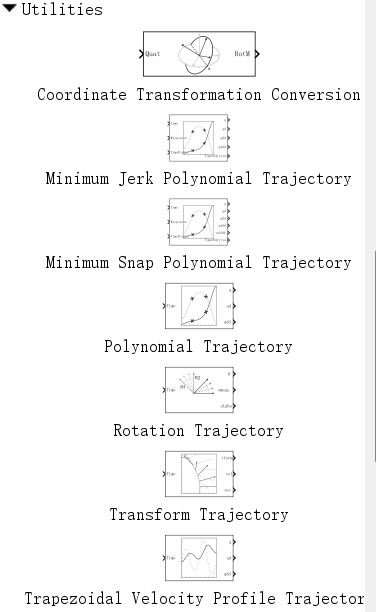
其中 Coordinate Transformation Conversion(坐标变换转换)极为重要,当我们想要指定机器人的末端坐标的位置变化时,能够使用它对信号编辑器输出的平移向量和旋转向量信号进行齐次变化矩阵(这个是描述机器运动的重要元素,不懂可以参考b站台湾老师的机械臂课程)再送入逆解算法。
| 轨迹类型 | 它是做什么的? | 核心目标与特点 | 典型应用场景 |
|---|---|---|---|
| Coordinate Transformation Conversion (坐标变换转换) | 基础工具。在不同坐标系(如世界坐标系、机器人基座标系、工具坐标系)之间进行位置和姿态的转换计算。 | 实现运动描述的转换,是所有高级轨迹规划的前提。它不直接规划路径,而是为路径规划提供数学基础。 | 计算机器人末端执行器相对于其底座的位置,或将一个在相机坐标系中识别到的目标点转换到机器人坐标系中去抓取。 |
| Polynomial Trajectory (多项式轨迹) | 通用平滑轨迹。使用多项式函数(如3次、5次)来描述位置随时间的变化。 | 在起点和终点满足指定的位置、速度等边界条件,实现基本的光滑运动,避免速度突变。 | 机械臂点到点移动、3D打印机喷头移动等需要运动连续、无冲击的场合。 |
| Minimum Jerk Polynomial Trajectory (最小冲击多项式轨迹) | 优化舒适度/平滑度。在多项式轨迹的基础上,优化其系数,使得运动过程中的"加加速度"(加速度的导数)最小。 | 追求运动的极致平滑,减少振动和冲击。这对乘坐舒适性(如机器人载人)或对运动平稳性要求高的任务至关重要。 | 机器人搬运易碎物品、手术机器人、无人机搭载相机进行拍摄、豪华轿车的自动驾驶调节。 |
| Minimum Snap Polynomial Trajectory (最小加速度变化率轨迹) | 优化能量效率/柔顺性。优化多项式系数,使得"加加加速度"(加速度的二次导数)最小。 | 在平滑的基础上,进一步降低加速度的变化率,通常能使执行器能耗更优,运动更柔顺。 | 多旋翼无人机、四足机器人的轨迹规划,以减少电机频繁调节带来的能耗和抖动。 |
| Trapezoidal Velocity Profile Trajectory (梯形速度曲线轨迹) | 追求时间最优 。将运动过程简单划分为匀加速、匀速、匀减速三个阶段,速度曲线呈梯形。 | 在电机/执行器的速度、加速度限制 下,以最短时间完成点到点移动。计算简单,但加速度不连续。 | 数控机床的快速定位、仓库AGV小车搬运、对运动时间敏感但平滑性要求不高的工业场景。 |
| Rotation Trajectory (旋转轨迹) | 专门规划旋转 。规划物体绕自身轴旋转的角度变化,例如从角度A平滑旋转到角度B。 | 专注于处理纯旋转运动的插值和规划,与位置规划分开。 | 机器人手腕的转动、相机云台的俯仰/偏航、螺丝拧紧作业。 |
| Transform Trajectory (变换轨迹) | 同时规划位移和旋转 。同时规划物体的位置(X,Y,Z)和姿态(旋转),使其从一个"位姿"平滑变化到另一个"位姿"。 | 处理完整的6自由度运动(3个平移+3个旋转),是机器人末端抓取、装配等复杂任务的完整运动描述。 | 机械臂从桌面抓起一个杯子并放入指定位置,需要同时移动和转动杯子。 |
机器人运动学动力学解算
机器人运动学动力学解算离不开运动学和动力学的支撑
常见的几个模块如下:
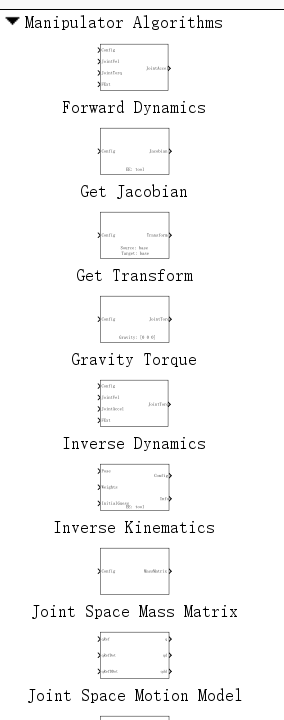
| 算法类别 | 代表性算法 | 核心功能描述 | 典型应用场景 |
|---|---|---|---|
| 运动学 (Kinematics) | Forward Kinematics (正向运动学) | **已知关节角度,计算机械臂末端的位置和姿态。** 这是从关节空间到任务空间的映射。 | 仿真中实时显示机械臂的形态;验证机构设计。 |
| Inverse Kinematics (逆运动学) | **已知末端目标位姿,反解出所需的关节角度。** 这是从任务空间到关节空间的映射,是控制机械臂到达目标的关键。 | 让机械臂末端移动到指定的位置抓取物体;轨迹规划的第一步。 | |
| Get Jacobian (获取雅可比矩阵) | 计算描述末端线速度/角速度 与各关节速度之间线性关系的矩阵。 | 速度控制、奇异性分析、实现笛卡尔空间(末端)的直接运动控制。 | |
| Get Geometric Jacobian (获取几何雅可比) | 基于几何关系(连杆参数)计算雅可比矩阵,是标准方法。 | 同"Get Jacobian",是更基础的实现方式。 | |
| 动力学 (Dynamics) | Forward Dynamics (正向动力学) | **已知关节扭矩/力,计算关节的加速度、速度与位置。** 即"给定力,求运动"。 | 机械臂的动力学仿真,预测在给定驱动力下机械臂的实际运动。 |
| Inverse Dynamics (逆动力学) | **已知期望的关节运动(位置、速度、加速度),计算所需的关节扭矩/力。** 即"给定运动,求所需的力"。 | 计算实现特定轨迹所需的电机扭矩;计算重力补偿、前馈控制。 | |
| 轨迹生成 (Trajectory Generation) | 图表中虽未具体列出,但通常包含多种插值算法。 | 根据给定的路径点(中间点),生成一条平滑、连续、可执行的关节角度或末端位姿随时间变化的曲线。 | 规划机械臂从A点到B点的运动过程,确保运动平稳、无冲击。 |
| 碰撞检测 (Collision Detection) | 图表中虽未具体列出,但这是关键模块。 | 检测机械臂连杆之间、或机械臂与环境中的物体之间是否发生干涉或碰撞。 | 保障仿真与实物运行的安全,实现避障规划。 |
| 控制与仿真 (Control & Simulation) | 包含状态估计、控制器(如PID)、传感器接口等。 | 实现闭环控制,使机械臂能精确跟踪期望的轨迹,并处理传感器反馈。 | 整个机械臂系统的实时控制与仿真循环。 |
| 系统与管理 (System & Management) | 包含模型加载、参数配置、日志记录、UI/ROS接口等。 | 负责算法模块的集成、调度、数据交换和人机交互。 | 支撑整个软件框架的运行,是算法的"粘合剂"和"调度中心"。 |
需要注意的点
在规划机器人的正逆解的时候,我们需要为模块提供需要的正逆解的模型,这需要我们自行生成。
生成步骤如下:1.新建一个脚本(.m文件) 2.接着输入以下代码
cpp
Ts = 0.001;
[模型名字,ArmInfo] = importrobot('模型所在文件');举一个例子
cpp
Ts = 0.001;
[DOF3_RRR,ArmInfo] = importrobot('DOF2_MODULE');最后,有时候我们重新打开模型会提示所选模型不存在的情况,重新运行.m又会报错,只是因为.m生成的模型中不包含原来最基本的元素了,这时,只需要删除除了模型以外的元素然后运行脚本,待脚本运行之后再撤销之前的删除。
控制器设计
这个自行实现
其他重要模块以及观察发现
connect port
想要观察一个物体的测量数值,可以通过一个connection port 引入子系统外部,在子系统的外部使用py-to-sim模块将测量量单位转化
spatial contact force
在绘制的斜坡和机器人之间常常会看见 spatial contact force的模块
-
功能 :用于模拟三维空间中任意形状刚体之间的接触。这是更通用、更强大的模块,可以处理真实的3D碰撞,比如一个球掉进一个碗里,或者机械臂的末端效应器抓取一个方块。
-
工作原理:它可以基于您定义的三维几何体(如球体、立方体、圆柱体、网格文件等)进行精确的碰撞检测,并计算三维空间中的接触力和力矩。
-
图标解读:图标与平面模块类似,但功能扩展到三维空间。背景高亮(浅蓝色)可能表示这是库中推荐或更常用的模块,或者是您当前选中的模块。
另外还有一个平面的,叫做planar contact force,这两个之间的关系如下:
核心区别与选择
| 特性 | 平面接触力 | 空间接触力 |
|---|---|---|
| 维度 | 二维平面 | 三维空间 |
| 应用场景 | 平面机构、二维仿真 | 通用三维多体系统 |
| 几何定义 | 二维轮廓(线、圆、多边形) | 三维几何体(球、圆柱、CAD网格等) |
| 计算效率 | 相对较高 | 相对较低(更复杂) |
| 输出力 | 平面内的法向力与摩擦力 | 三维空间中的力矢量与力矩矢量 |
模型显示窗口
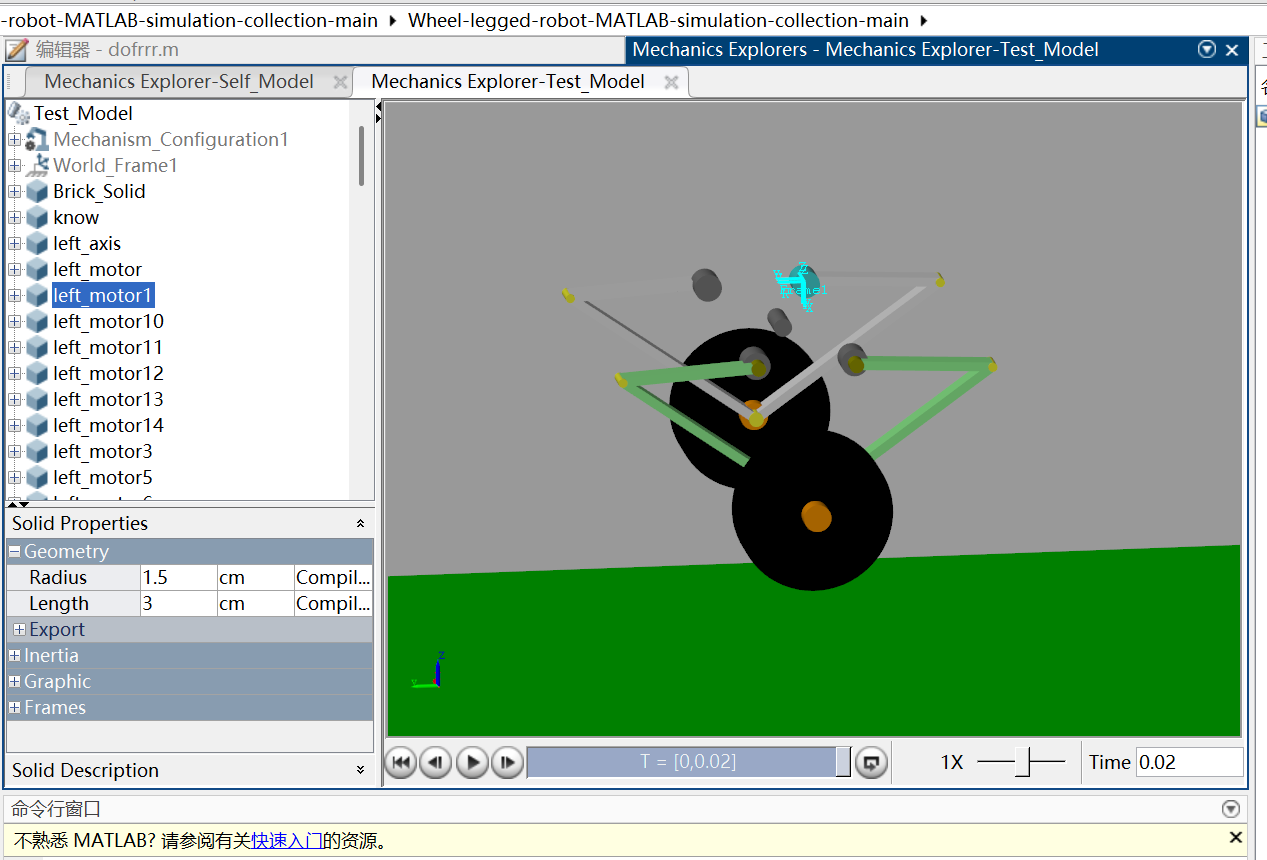
模型的显示串口可以在主窗口中显示,如果用户在模拟的过程中想去写脚本代码可以点击编辑器那一栏切换。
在模型左侧显示各个刚体和连接件,在观察开源模型的时候可以点击左侧的刚体和连接件(前提需要我们先命名),另外调试的时候可以通过注销某个模型来逐个排查。
学习资料分享
1.仿真建模
如何使用MATLAB 2021设计机器人|SimScape工具箱|机器人系统工具箱_哔哩哔哩_bilibili
2.机器人学
【机器人理论最好中文入门课程 没有之一】 机械臂 系统 结构 旋转矩阵 变换矩阵 DH模型 运动学正逆解 轨迹规划 动力学 控制 遥控操作 教程_哔哩哔哩_bilibili