
三、深度学习
4、激活函数
激活函数的主要作用是对神经元获得的输入进行非线性变换,以此反映神经元的非线性特性。常见的激活函数有线性激活函数、符号激活函数、Sigmod激活函数、双曲正切激活函数、高斯激活函数、ReLU激活函数。
(1)线性激活函数
F(x)=kx+c,其中k和c是常量、线性函数常用在线性神经网络中。
(2)符号激活函数
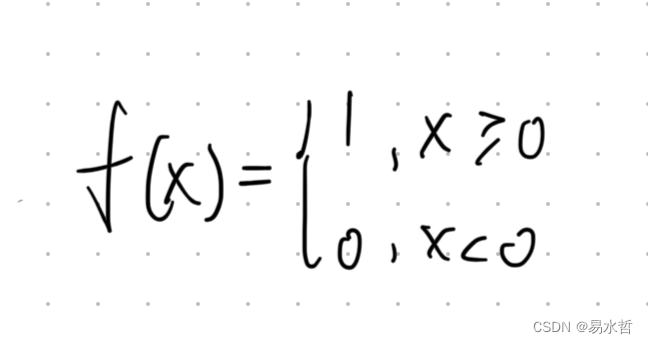
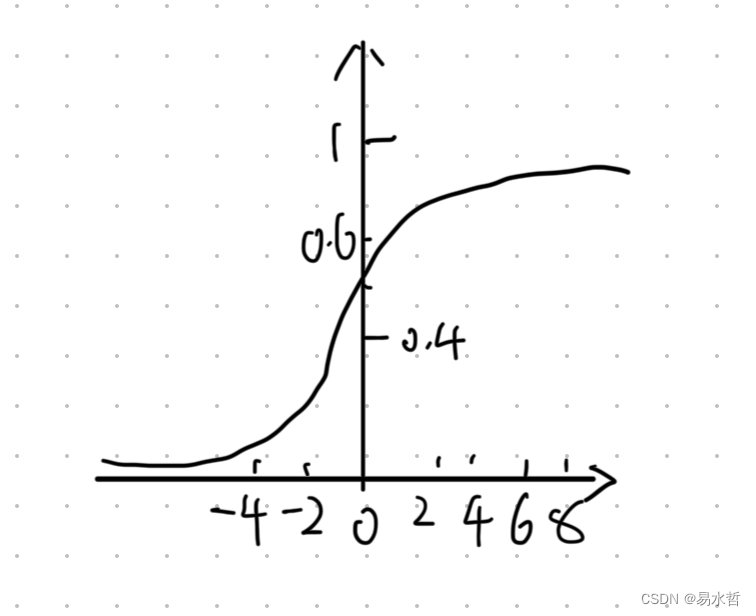
(3)Sigmod激活函数
Sigmod函数又称为S形函数,是最为常见的激活函数:
 其图像如下
其图像如下
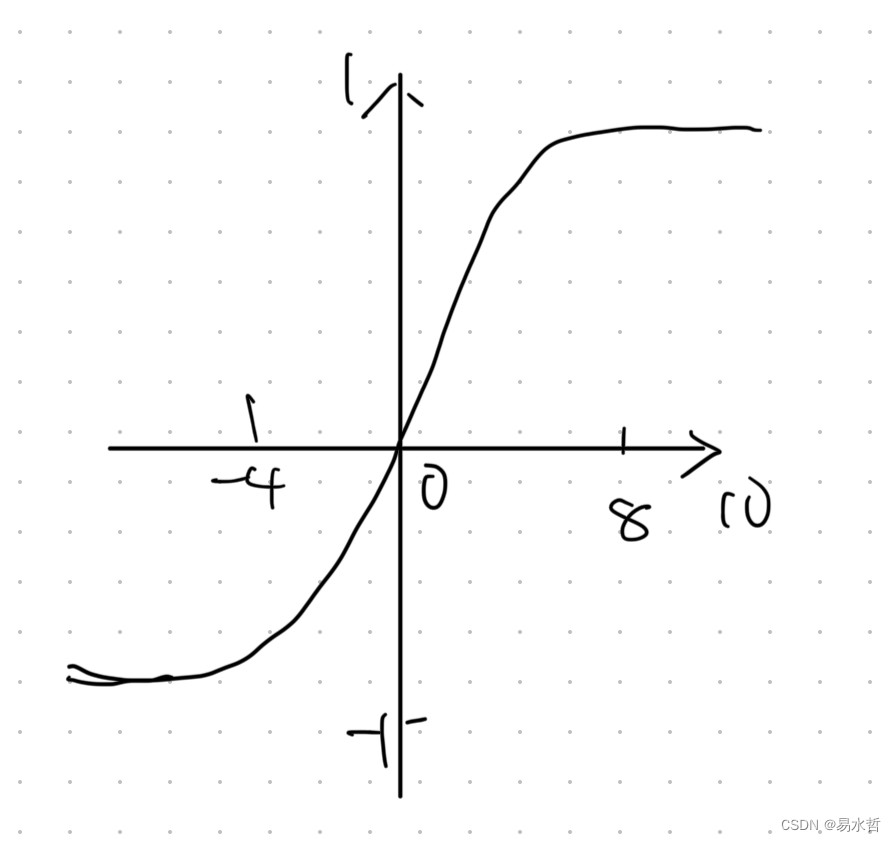
(4)双曲正切激活函数

图像如下所示:
(5)高斯激活函数
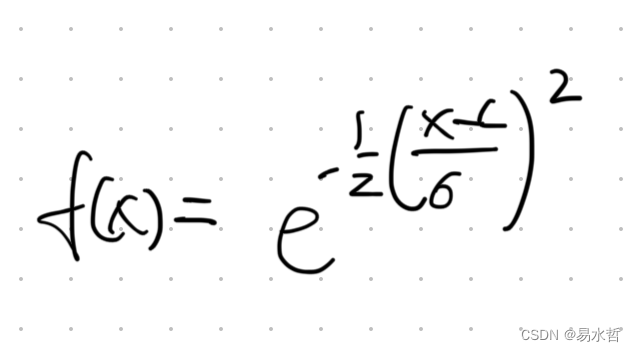
(6)ReLU激活函数
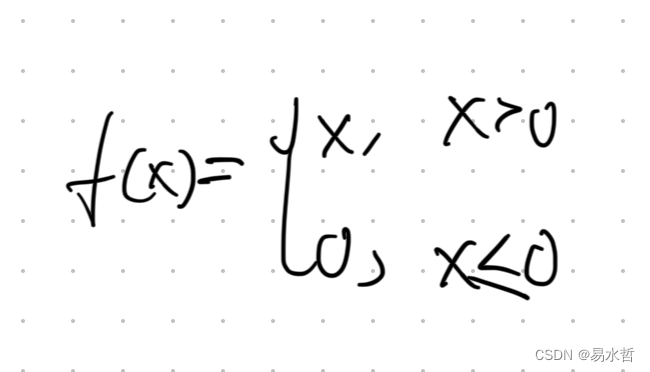
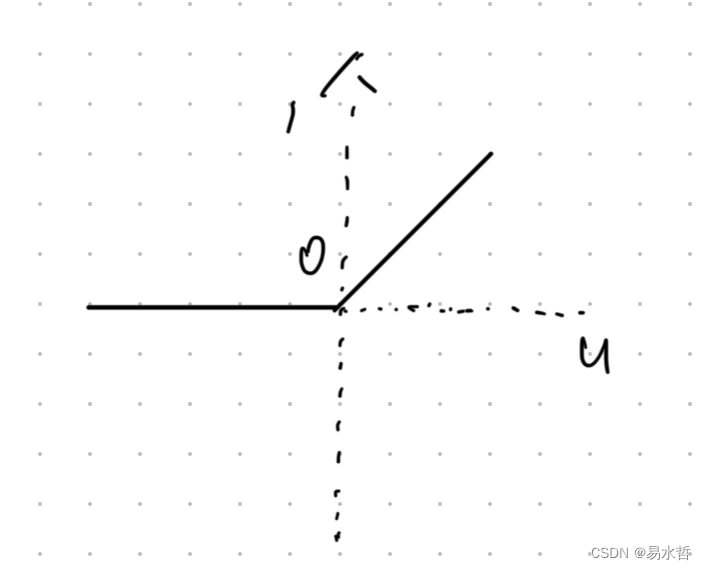
也可以表示为F(x)=max(0,x),图像如下图所示:
在神经网络中,ReLU激活函数得到广泛应用,尤其在卷积神经网络中,往往不选择Sigmod或Tanh而选择ReLU,原因主要有以下几点:
a、Sigmod函数求导涉及指数,计算复杂,ReLU代价小,计算速度快。
b、Sigmod函数导数最大值为1/4,链式求导会导致梯度越来越小,训练深度神经网络容易导致梯度消失,但是ReLU函数的导数为1,不会出现梯度消失。
c、有研究表明,人脑在工作时大概只有5%的神经元被激活,而Sigmod函数激活比例是50%,人工神经网络理想状态下激活率为15%-30%,ReLU函数在小于0时完全不激活,可以适应理想网络的激活率要求。
5、梯度下降法
梯度下降法是神经网络模型训练中最常用的优化算法之一,将其应用于寻找损失函数或代价函数的极值点。
常见的梯度下降法有批量下降法、随机梯度下降法和小批量梯度下降法,一般采用小批量梯度下降法。
(1)批量梯度下降法
此方法是最原始的形式,它是指在每一次迭代时使用所有样本来进行梯度的更新。
优点:
a、每次更新使用全部样本,能更准确的朝向极值所在的方向,如果目标函数是凸函数,一定能收敛到全局最小值。
b、它对梯度的无偏估计,样例越多,估计越准确。
c、以此迭代时对所有样本进行计算,可以利用向量化操作实现并行。
缺点:
a、遍历计算所有样本不仅耗时还消耗大量资源。
b、每次更新遍历所有样本,有一些样本对参数更新价值不大。
c、如果是非凸函数,可能会陷入局部最小值。
迭代曲线如下:
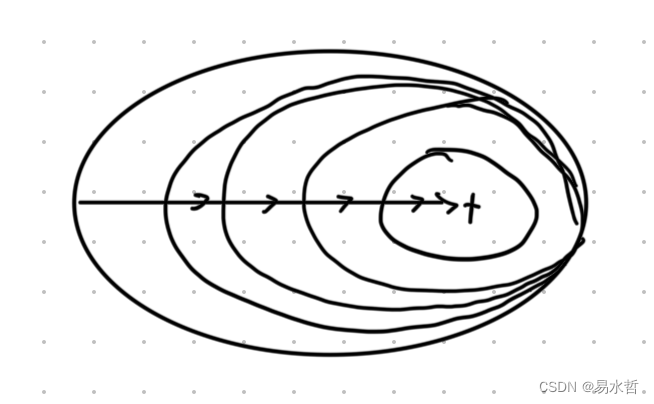
(2)随机梯度下降
每次迭代时只使用一个样本对参数进行更新。
优点:
a、每次只计算一个样本,更新速度大大加快。
b、在学习过程中加入了噪声和随机性,提高了泛化误差。
c、对于非凸函数,它的随机性有助于逃离某些不理想的局部最小值,获得全局最优解。
缺点:
a、更新所有样本需要大量时间。
b、学习过程波动较大。
迭代曲线如下:
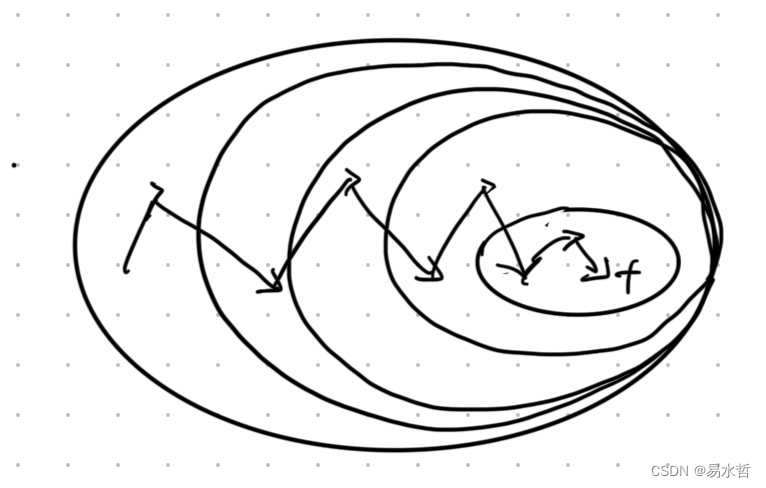
6、交叉熵损失函数
神经网络中分类问题较常使用交叉熵作为损失函数,二分类问题中公式如下,y*表示为真实标签,y表示预测标签:

多分类问题中公式可以写成下面形式:
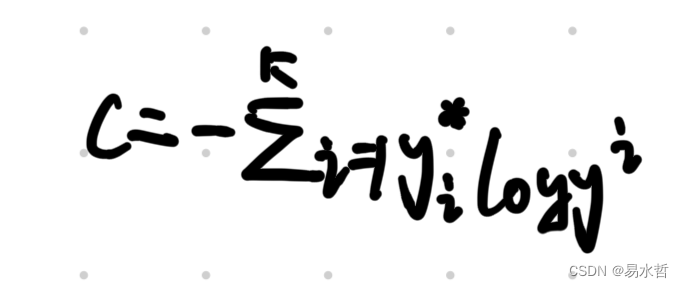
二分类的交叉熵python实现如下:
def binary_crossentropy(t,o):
#y_true是真实标签,y_pred是预测值
return -(y_true * np.log(y_pred)+(1-y_true)*np.log(1-y_pred))