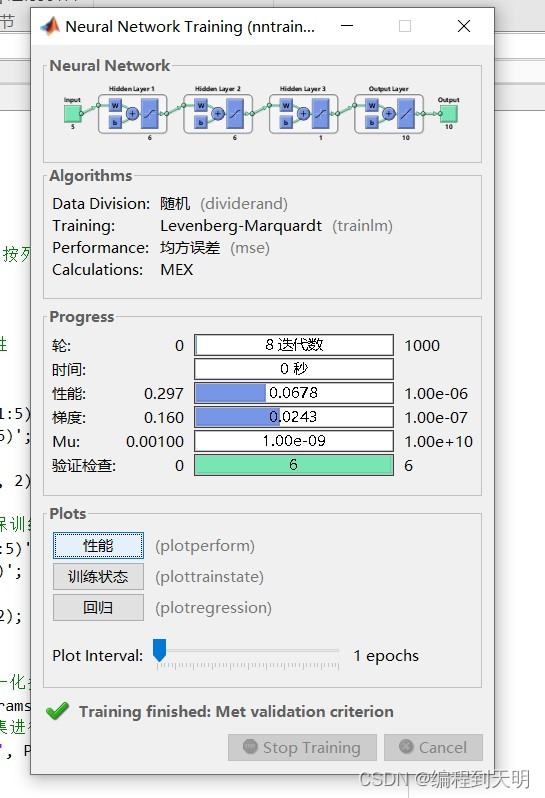
BP神经网络,即反向传播(Backpropagation)神经网络,是一种多层前馈神经网络,它通过反向传播算法来更新网络权重。这种网络结构特别适合于分类和回归任务。
MATLAB环境设置
在开始之前,请确保MATLAB环境已经设置好,并且安装了神经网络工具箱。
同时,写下基础代码:
Matlab
% 清空环境变量并关闭警告消息
warning off;
clear;
clc;数据导入与预处理
数据是机器学习的核心。在本例中,我们将从一个名为data.xlsx的Excel文件中导入数据。假设数据集中前5列是输入特征,第6列是输出标签。
Matlab
% 划分训练集和测试集
% 使用随机排列来确保数据的随机性
indices = randperm(10);
% 取前10个数据作为训练集
P_train = data(indices(1:10), 1:5)';
T_train = data(indices(1:10), 6)';
% 计算训练集的大小
numTrainSamples = size(P_train, 2);
% 测试集使用相同的随机排列,确保训练集和测试集的一致性
P_test = data(indices(1:10), 1:5)';
T_test = data(indices(1:10), 6)';
% 计算测试集的大小
numTestSamples = size(P_test, 2);接下来,我们需要划分数据为训练集和测试集,并对数据进行归一化处理以提高训练效率。
Matlab
% 数据归一化处理
% 对训练集进行归一化,并保存归一化参数
[P_train_norm, normalizationParams] = mapminmax(P_train, 0, 1);
% 使用训练集的归一化参数对测试集进行归一化
P_test_norm = mapminmax('apply', P_test, normalizationParams);
% 将输出数据进行独热编码
T_train_encoded = ind2vec(T_train);
T_test_encoded = ind2vec(T_test);建立BP神经网络模型
在MATLAB中,我们可以使用newff函数来快速建立一个BP神经网络模型。这个函数允许我们指定输入、输出和隐藏层的大小。
Matlab
% 建立神经网络模型
% 使用新的前馈网络函数newff,输入为归一化后的训练集特征,输出为编码后的输出数据
net = newff(P_train_norm, T_train_encoded, [6 6 1]);设置训练参数
在训练神经网络之前,我们需要设置一些训练参数,如迭代次数、目标训练误差和学习率。
Matlab
% 设置训练参数
% 包括训练的迭代次数、训练误差目标和学习率
net.trainParam.epochs = 1000; % 迭代次数
net.trainParam.goal = 1e-6; % 目标训练误差
net.trainParam.lr = 0.01; % 学习率训练神经网络
使用train函数对网络进行训练。这个过程可能需要一些时间,具体取决于数据集的大小和网络的复杂性。
Matlab
% 开始训练
% 使用train函数对网络进行训练
net = train(net, P_train_norm, T_train_encoded);测试与性能评价
训练完成后,我们使用测试集来评估模型的性能。我们还将计算训练集和测试集的准确率。
Matlab
% 进行测试
% 使用sim函数对训练集和测试集进行模拟
T_train_sim = sim(net, P_train_norm);
T_test_sim = sim(net, P_test_norm);
% 反归一化处理
% 将模拟结果从独热编码转换回原始类别
T_train_decoded = vec2ind(T_train_sim);
T_test_decoded = vec2ind(T_test_sim);
% 性能评价
% 计算训练集和测试集的准确率
trainAccuracy = sum(T_train_decoded == T_train) / numTrainSamples * 100;
testAccuracy = sum(T_test_decoded == T_test) / numTestSamples * 100;
% 打印性能评价结果
fprintf('训练集准确率: %.2f%%\n', trainAccuracy);
fprintf('测试集准确率: %.2f%%\n', testAccuracy);效果展示