目录
- [第三门课 结构化机器学习项目(Structuring Machine Learning Projects)](#第三门课 结构化机器学习项目(Structuring Machine Learning Projects))
-
- [第一周 机器学习(ML)策略(1)(ML strategy(1))](#第一周 机器学习(ML)策略(1)(ML strategy(1)))
-
- [1.9 可避免偏差(Avoidable bias)](#1.9 可避免偏差(Avoidable bias))
- [1.10 理解人的表现(Understanding human-level performance)](#1.10 理解人的表现(Understanding human-level performance))
第三门课 结构化机器学习项目(Structuring Machine Learning Projects)
第一周 机器学习(ML)策略(1)(ML strategy(1))
1.9 可避免偏差(Avoidable bias)
我们讨论过,你希望你的学习算法能在训练集上表现良好,但有时你实际上并不想做得太好。你得知道人类水平的表现是怎样的,可以确切告诉你算法在训练集上的表现到底应该有多好,或者有多不好,让我告诉你是什么意思吧。
我们经常使用猫分类器来做例子,比如人类具有近乎完美的准确度,所以人类水平的错误是 1%。在这种情况下,如果您的学习算法达到 8%的训练错误率和 10%的开发错误率,那么你也许想在训练集上得到更好的结果。所以事实上,你的算法在训练集上的表现和人类水平的表现有很大差距的话,说明你的算法对训练集的拟合并不好。所以从减少偏差和方差的工具这个角度看,在这种情况下,我会把重点放在减少偏差上。你需要做的是,比如说训练更大的神经网络,或者跑久一点梯度下降,就试试能不能在训练集上做得更好。

但现在我们看看同样的训练错误率和开发错误率,假设人类的表现不是 1%,我们就把它抄写过来。但你知道,在不同的应用或者说用在不同的数据集上,假设人类水平错误实际上是 7.5%,也许你的数据集中的图像非常模糊,即使人类都无法判断这张照片中有没有猫。这个例子可能稍微更复杂一些,因为人类其实很擅长看照片,分辨出照片里有没有猫。但就为了举这个例子,比如说你的数据集中的图像非常模糊,分辨率很低,即使人类错误率也达到 7.5%。在这种情况下,即使你的训练错误率和开发错误率和其他例子里一样,你就知道,也许你的系统在训练集上的表现还好,它只是比人类的表现差一点点。在第二个例子中,你可能希望专注减少这个分量,减少学习算法的方差,也许你可以试试正则化,让你的开发错误率更接近你的训练错误率。
所以在之前的课程关于偏差和方差的讨论中,我们主要假设有一些任务的贝叶斯错误率几乎为 0。所以要解释这里发生的事情,看看这个猫分类器,用人类水平的错误率估计或代替贝叶斯错误率或贝叶斯最优错误率,对于计算机视觉任务而言,这样替代相当合理,因为人类实际上是非常擅长计算机视觉任务的,所以人类能做到的水平和贝叶斯错误率相差不远。根据定义,人类水平错误率比贝叶斯错误率高一点,因为贝叶斯错误率是理论上限,但人类水平错误率离贝叶斯错误率不会太远。所以这里比较意外的是取决于人类水平错误率有多少,或者这真的就很接近贝叶斯错误率,所以我们假设它就是,但取决于我们认为什么样的水平是可以实现的。

在这两种情况下,具有同样的训练错误率和开发错误率,我们决定专注于减少偏差的策略或者减少方差的策略。那么左边的例子发生了什么? 8%的训练错误率真的很高,你认为你可以把它降到 1%,那么减少偏差的手段可能有效。而在右边的例子中,如果你认为贝叶斯错误率是 7.5%,这里我们使用人类水平错误率来替代贝叶斯错误率,但是你认为贝叶斯错误率接近 7.5%,你就知道没有太多改善的空间了,不能继续减少你的训练错误率了,你也不会希望它比 7.5%好得多,因为这种目标只能通过可能需要提供更进一步的训练。而这边,就还(训练误差和开发误差之间)有更多的改进空间,可以将这个 2%的差距缩小一点,使用减少方差的手段应该可行,比如正则化,或者收集更多的训练数据。
所以要给这些概念命名一下,这不是广泛使用的术语,但我觉得这么说思考起来比较流畅。就是把这个差值,贝叶斯错误率或者对贝叶斯错误率的估计和训练错误率之间的差值称为可避免偏差,你可能希望一直提高训练集表现,直到你接近贝叶斯错误率,但实际上你也不希望做到比贝叶斯错误率更好,这理论上是不可能超过贝叶斯错误率的,除非过拟合。而这个训练错误率和开发错误率之前的差值,就大概说明你的算法在方差问题上还有多少改善空间。

可避免偏差这个词说明了有一些别的偏差,或者错误率有个无法超越的最低水平,那就是说如果贝叶斯错误率是 7.5%。你实际上并不想得到低于该级别的错误率,所以你不会说你的训练错误率是 8%,然后 8%就衡量了例子中的偏差大小。你应该说,可避免偏差可能在0.5%左右,或者 0.5%是可避免偏差的指标。而这个 2%是方差的指标,所以要减少这个 2%比减少这个 0.5%空间要大得多。而在左边的例子中,这 7%衡量了可避免偏差大小,而 2%衡量了方差大小。所以在左边这个例子里,专注减少可避免偏差可能潜力更大。
所以在这个例子中,当你理解人类水平错误率,理解你对贝叶斯错误率的估计,你就可以在不同的场景中专注于不同的策略,使用避免偏差策略还是避免方差策略。在训练时如何考虑人类水平表现来决定工作着力点,具体怎么做还有更多微妙的细节,所以在下一个视频中,我们会深入了解人类水平表现的真正意义。
1.10 理解人的表现(Understanding human-level performance)
人类水平表现这个词在论文里经常随意使用,但我现在告诉你这个词更准确的定义,特别是使用人类水平表现这个词的定义,可以帮助你们推动机器学习项目的进展。还记得上个视频中,我们用过这个词"人类水平错误率"用来估计贝叶斯误差,那就是理论最低的错误率,任何函数不管是现在还是将来,能够到达的最低值。我们先记住这点,然后看看医学图像分类例子。

假设你要观察这样的放射科图像,然后作出分类诊断,假设一个普通的人类,未经训练的人类,在此任务上达到 3%的错误率。普通的医生,也许是普通的放射科医生,能达到 1%的错误率。经验丰富的医生做得更好,错误率为 0.7%。还有一队经验丰富的医生,就是说如
果你有一个经验丰富的医生团队,让他们都看看这个图像,然后讨论并辩论,他们达成共识的意见达到 0.5%的错误率。所以我想问你的问题是,你应该如何界定人类水平错误率?人类水平错误率 3%,1%, 0.7%还是 0.5%?
你也可以暂停视频思考一下,要回答这个问题,我想请你记住,思考人类水平错误率最有用的方式之一是,把它作为贝叶斯错误率的替代或估计。如果你愿意,也可以暂停视频,思考一下这个问题。
但这里我就直接给出人类水平错误率的定义,就是如果你想要替代或估计贝叶斯错误率,那么一队经验丰富的医生讨论和辩论之后,可以达到 0.5%的错误率。我们知道贝叶斯错误率小于等于 0.5%,因为有些系统,这些医生团队可以达到 0.5%的错误率。所以根据定义,最优错误率必须在 0.5%以下。我们不知道多少更好,也许有一个更大的团队,更有经验的医生能做得更好,所以也许比 0.5%好一点。但是我们知道最优错误率不能高于 0.5%,那么在这个背景下,我就可以用 0.5%估计贝叶斯错误率。所以我将人类水平定义为 0.5%,至少如果你希望使用人类水平错误来分析偏差和方差的时候,就像上个视频那样。
现在,为了发表研究论文或者部署系统,也许人类水平错误率的定义可以不一样,你可以使用 1%,只要你超越了一个普通医生的表现,如果能达到这种水平,那系统已经达到实用了。也许超过一名放射科医生,一名医生的表现,意味着系统在一些情况下可以有部署价值了。
本视频的要点是,在定义人类水平错误率时,要弄清楚你的目标所在,如果要表明你可以超越单个人类,那么就有理由在某些场合部署你的系统,也许这个定义是合适的。但是如果您的目标是替代贝叶斯错误率,那么这个定义(经验丰富的医生团队------0.5%)才合适。

要了解为什么这个很重要,我们来看一个错误率分析的例子。比方说,在医学图像诊断例子中,你的训练错误率是 5%,你的开发错误率是 6%。而在上一张幻灯片的例子中,我们的人类水平表现,我将它看成是贝叶斯错误率的替代品,取决于你是否将它定义成普通单个医生的表现,还是有经验的医生或医生团队的表现,你可能会用 1%或 0.7%或 0.5%。同时也回想一下,前面视频中的定义,贝叶斯错误率或者说贝叶斯错误率的估计和训练错误率直接的差值就衡量了所谓的可避免偏差,这(训练误差与开发误差之间的差值)可以衡量或者估计你的学习算法的方差问题有多严重。
所以在这个第一个例子中,无论你做出哪些选择,可避免偏差大概是 4%,这个值我想介于......,如果你取 1%就是 4%,如果你取 0.5%就是 4.5%,而这个差距(训练误差与开发误差之间的差值)是 1%。所以在这个例子中,我得说,不管你怎么定义人类水平错误率,使用单个普通医生的错误率定义,还是单个经验丰富医生的错误率定义或经验丰富的医生团队的错误率定义,这是 4%还是 4.5%,这明显比都比方差问题更大。所以在这种情况下,你应该专注于减少偏差的技术,例如培训更大的网络。

现在来看看第二个例子,比如说你的训练错误率是 1%,开发错误率是 5%,这其实也不怎么重要,这种问题更像学术界讨论的,人类水平表现是 1%或 0.7%还是 0.5%。因为不管你使用哪一个定义,你测量可避免偏差的方法是,如果用那个值,就是 0%到 0.5%之前,对吧?
那就是人类水平和训练错误率之前的差距,而这个差距是 4%,所以这个 4%差距比任何一种定义的可避免偏差都大。所以他们就建议,你应该主要使用减少方差的工具,比如正则化或者去获取更大的训练集。
什么时候真正有效呢?
就是比如你的训练错误率是 0.7%,所以你现在已经做得很好了,你的开发错误率是 0.8%。在这种情况下,你用 0.5%来估计贝叶斯错误率关系就很大。因为在这种情况下,你测量到的可避免偏差是 0.2%,这是你测量到的方差问题 0.1%的两倍,这表明也许偏差和方差都存
在问题。但是,可避免偏差问题更严重。在这个例子中,我们在上一张幻灯片中讨论的是 0.5%,就是对贝叶斯错误率的最佳估计,因为一群人类医生可以实现这一目标。如果你用 0.7 代替贝叶斯错误率,你测得的可避免偏差基本上是 0%,那你就可能忽略可避免偏差了。实际上你应该试试能不能在训练集上做得更好。
我希望讲这个能让你们有点概念,知道为什么机器学习问题上取得进展会越来越难,当你接近人类水平时进展会越来越难。
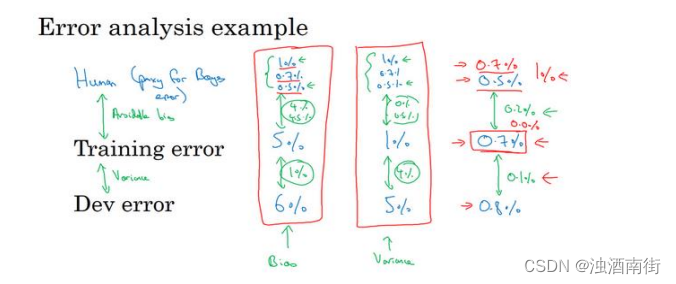
在这个例子中,一旦你接近 0.7%错误率,除非你非常小心估计贝叶斯错误率,你可能无法知道离贝叶斯错误率有多远,所以你应该尽量减少可避免偏差。事实上,如果你只知道单个普通医生能达到 1%错误率,这可能很难知道是不是应该继续去拟合训练集,这种问题只会出现在你的算法已经做得很好的时候,只有你已经做到 0.7%, 0.8%, 接近人类水平时会出现。
而在左边的两个例子中,当你远离人类水平时,将优化目标放在偏差或方差上可能更容易一点。这就说明了,为什么当你们接近人类水平时,更难分辨出问题是偏差还是方差。所以机器学习项目的进展在你已经做得很好的时候,很难更进一步。

总结一下我们讲到的,如果你想理解偏差和方差,那么在人类可以做得很好的任务中,你可以估计人类水平的错误率,你可以使用人类水平错误率来估计贝叶斯错误率。所以你到贝叶斯错误率估计值的差距,告诉你可避免偏差问题有多大,可避免偏差问题有多严重,而训练错误率和开发错误率之间的差值告诉你方差上的问题有多大,你的算法是否能够从训练集泛化推广到开发集。
今天讲的和之前课程中见到的重大区别是,以前你们比较的是训练错误率和 0%,直接用这个值估计偏差。相比之下,在这个视频中,我们有一个更微妙的分析,其中并没有假设你应该得到 0%错误率,因为有时贝叶斯错误率是非零的,有时基本不可能做到比某个错误率阈值更低。所以在之前的课程中,我们测量的是训练错误率,然后观察的是训练错误率比0%高多少,就用这个差值来估计偏差有多大。而事实证明,对于贝叶斯错误率几乎是 0%的问题这样就行了,例如识别猫,人类表现接近完美,所以贝叶斯错误率也接近完美。所以当贝叶斯错误率几乎为零时,可以那么做。但数据噪点很多时,比如背景声音很嘈杂的语言识别,有时几乎不可能听清楚说的是什么,并正确记录下来。对于这样的问题,更好的估计贝叶斯错误率很有必要,可以帮助你更好地估计可避免偏差和方差,这样你就能更好的做出决策,选择减少偏差的策略,还是减少方差的策略。
回顾一下,对人类水平有大概的估计可以让你做出对贝叶斯错误率的估计,这样可以让你更快地作出决定是否应该专注于减少算法的偏差,或者减少算法的方差。这个决策技巧通常很有效,直到你的系统性能开始超越人类,那么你对贝叶斯错误率的估计就不再准确了,但这些技巧还是可以帮你做出明确的决定。
现在,深度学习的令人兴奋的发展之一就是对于越来越多的任务,我们的系统实际上可以超越人类了。在下一个视频中,让我们继续谈谈超越人类水平的过程。