目录
一、介绍
PCA(principal components analysis)即主成分分析技术,又称主分量分析,旨在利用降维的思想,把多指标转化为少数几个综合指标。
本使用采用的是鸢尾花数据集,需要把鸢尾花的四个数据特征转化为两个数据特征使得他可以在坐标轴上面显示出来。
二、算法流程
(1)数据中心化
对原始数据进行中心化处理,即将每个特征的值减去该特征的均值,以保证数据的均值为零。
pj = np.mean(X, axis=0)
X_pj = X - pj也就是说将每个数据减去他的平均值得到新的数据。代码先计算他的平均值,再对每个数据减去他的平均值。
(2)计算协方差矩阵
找到一个轴,使得样本空间的所有点映射到这个轴的协方差最大。
公式:
n = X.shape[0]
cov = np.dot(X_pj.T,X_pj) / (n - 1)因为事先已经对他进行了数据中心化,所以得到的协方差就可以不用求解平均值,而直接np.dot(X_pj.T,X_pj)就得到第i个特征和第j个特征的协方差。除以(n-1)是为了得到无偏估计,这样求解准确度会更高。
(3)特征值分解
对矩阵A进行特征值分解就是将方阵分解为其特征值和特征向量的过程。
公式:
其中V就是特征值,lambda就是特征向量。
学习了代码后使用QR分解法来求解特征值和特征向量。
原理:
上三角形是对角线下方的值全部为零,上三角形的对角线就是他的特征值。我们通过不断把A进行相似矩阵转化,他的特征值是不会变的,通过迭代多次最后吧矩阵A转化为上三角形,就可以直接得到他的特征值了,特征向量就是变换过程中Q的累乘。
def qr_algorithm(A, num=1000, tol=1e-6):
n = A.shape[0]
tzxl = np.eye(n)
for i in range(num):
Q, R = np.linalg.qr(A)
A = np.dot(R, Q)
tzxl = np.dot(tzxl, Q)
t = np.sqrt(np.sum(np.square(A) - np.sum(np.square(np.diag(A)))))
if t < tol:
break
tzz = np.diag(A)
return tzz, tzxl- 初始化特征向量为单位矩阵
- 迭代num次使得
- 对矩阵A进行 QR 分解,得到正交矩阵Q和上三角矩阵R,不断对特征向量进行更新A成为他的相似矩阵。
- 非对角线元素的范数,如果小到一定值,就说明更新差不多完成了,就退出循环。
- 最后特征值就是A对角线上的值,特征向量就是累乘。
(4)选择特征
我们已经得到了特征向量,先对他进行排序,选择最大的几个成分当作主成分,然后与中心化的X_pj相乘得到新的、降维后的数据集,然后就可以对降维后的数据集进行操作了。
t1 = np.argsort(-tzz)
tzxl = tzxl[:, t1]
cnt = 2
zcf = tzxl[:, :cnt]
X1 = np.dot(X_pj, zcf)三、运行结果展示
先将降维后的数据打印出来,可以看到已经变为样本二维的了。
打印出散点图
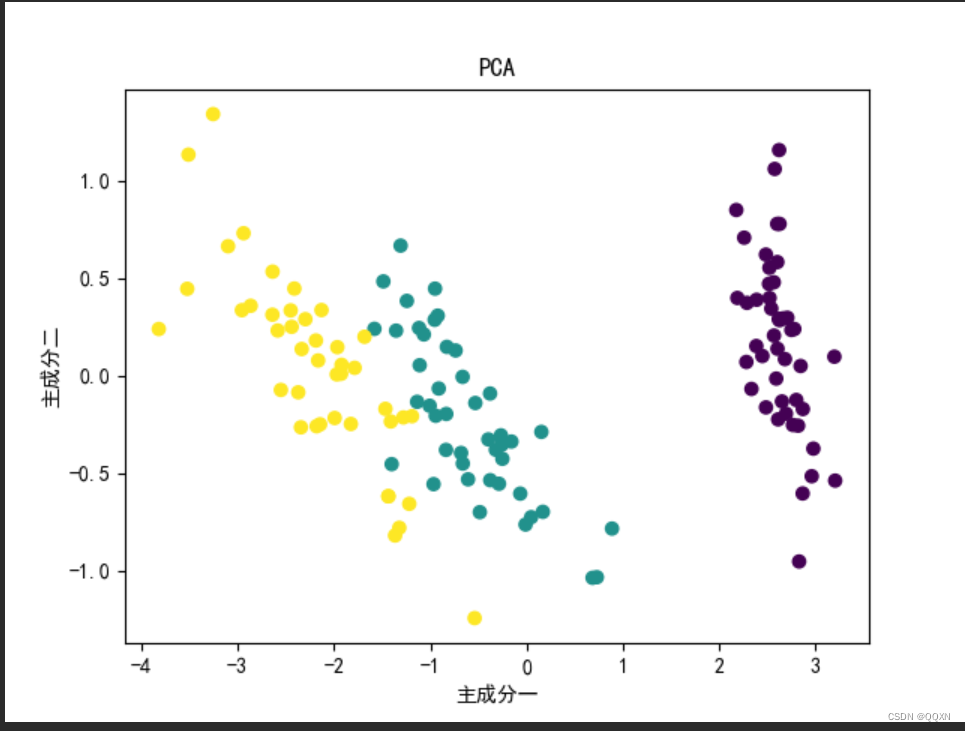
label_encoder = LabelEncoder()
y_encoded = label_encoder.fit_transform(y)
print(X1)
plt.rcParams['font.sans-serif'] = ['SimHei']
rcParams['axes.unicode_minus'] = False
plt.scatter(X1[:, 0], X1[:, 1], c=y_encoded, cmap='viridis')
plt.xlabel('主成分一')
plt.ylabel('主成分二')
plt.title('PCA')
plt.show()将y的标签映射为数值。并且需要加上plt.rcParams['font.sans-serif'] = ['SimHei']和rcParams['axes.unicode_minus'] = False来保证中文和负号在图像中正常显示
四、实验中遇到的问题
因为这个实验的流程相对比较简短,主要的问题就是在特征值分解的理解上,刚开始因为直接计算特征值和特征向量的难度太大,没想到用相似矩阵来求解。后来使用QR分解法迭代求解特征值和特征向量就比较简便。
五、PCA的优缺点
优点:
- PCA可以将高维数据转化为低维,从而减少数据维度。可以降低计算复杂性和存储需求。
- PCA可以保留数据中最重要的特征,并且去除噪声和冗余信息。
缺点:
-
PCA假设数据之间的关系是线性的,因此它可能无法有效处理非线性关系的数据。
-
对于非常大的数据集,计算协方差矩阵和进行特征分解可能会非常耗时且计算复杂度较高。
-
在降维的过程中保留的主成分不可能包含所有信息,不可避免的的导致信息模糊,丢失。
六、总代码
import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
from matplotlib import rcParams
import matplotlib.pyplot as plt
from sklearn.preprocessing import LabelEncoder
train_data = pd.read_csv("C:\\Users\\李烨\\Desktop\\新建文件夹\\6\\iris.txt", sep='\s+')
# 假设数据集的最后一列是目标标签
X = train_data.iloc[:, :-1].values # 特征
y = train_data.iloc[:, -1].values # 标签
pj = np.mean(X, axis=0)
X_pj = X - pj
n = X.shape[0]
cov = np.dot(X_pj.T, X_pj) / (n - 1)
def QR(A, num=1000, tol=1e-6):
n = A.shape[0]
tzxl = np.eye(n)
for i in range(num):
Q, R = np.linalg.qr(A)
A = np.dot(R, Q)
tzxl = np.dot(tzxl, Q)
t = np.sqrt(np.sum(np.square(A) - np.sum(np.square(np.diag(A)))))
if t < tol:
break
tzz = np.diag(A)
return tzz, tzxl
tzz, tzxl = QR(cov)
t1 = np.argsort(-tzz)
tzxl = tzxl[:, t1]
cnt = 2
zcf = tzxl[:, :cnt]
X1 = np.dot(X_pj, zcf)
label_encoder = LabelEncoder()
y_encoded = label_encoder.fit_transform(y)
print(X1)
plt.rcParams['font.sans-serif'] = ['SimHei']
rcParams['axes.unicode_minus'] = False
plt.scatter(X1[:, 0], X1[:, 1], c=y_encoded, cmap='viridis')
plt.xlabel('主成分一')
plt.ylabel('主成分二')
plt.title('PCA')
plt.show()