我们之前讨论的多层感知机十分适合处理表格数据,其中行对应样本,列对应特征。
对于表格数据,我们寻找的模式可能涉及特征之间的交互,但是我们不能预先假设任何与特征交互相关的先验结构。 此时,多层感知机可能是最好的选择,然而对于高维感知数据,这种缺少结构的网络可能会变得不实用。
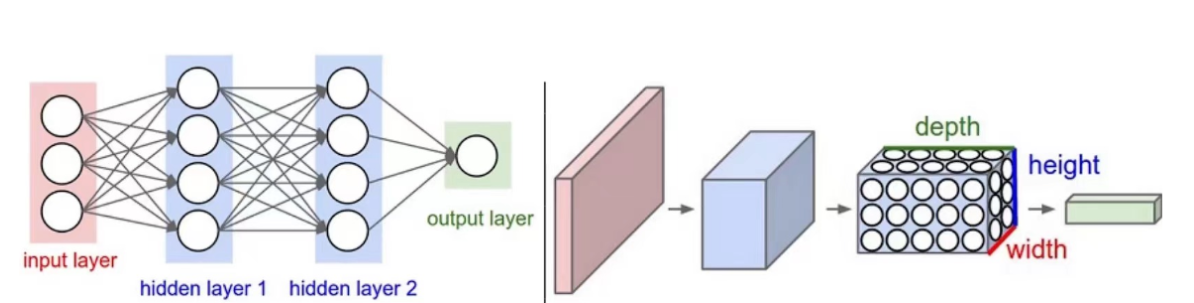
下图所示,左图是传统的神经网络(NN),右图就是卷积神经网络(Convolutional Neural Network)(CNN)。
我们在这张图中可以明显地看出,左图看上去像二维的,右图好像是一个三维的图。
举个例子,比如在传统神经网络输入的一张图有784个像素点,所以输入层就有784个 神经元 ,但在我们的 CNN 中输入的就是原始的图像28*28*1(是三维的),它是一个三维的矩阵。我们可以看到右图中又定义三维名称'height*width*depth'简称'h*w*d',接下来我们就围绕着卷积层和深度到底怎么变换展开。
例如,在猫狗分类的例子中:
假设我们有一个足够充分的照片数据集,数据集中是拥有标注的照片,每张照片具有百万级像素,这意味着网络的每次输入都有一百万个维度。 即使将隐藏层维度降低到1000,这个全连接层也将有10^9 个参数。 想要训练这个模型将不可实现,因为需要有大量的GPU、分布式优化训练的经验和超乎常人的耐心。

1. 卷积神经网络概述
计算机视觉 的 神经网络 架构:
-
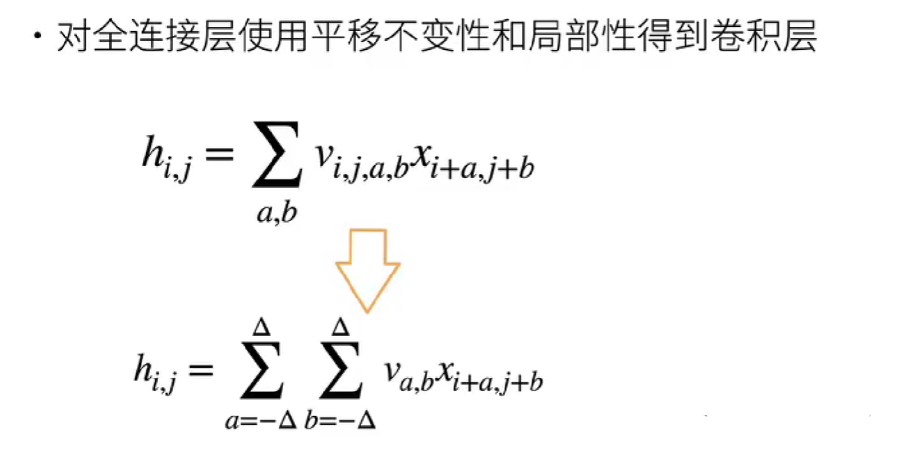
平移不变性(translation invariance):不管检测对象出现在图像中的哪个位置,神经网络的前面几层应该对相同的图像区域具有相似的反应,即为"平移不变性"。
-
局部性(locality):神经网络的前面几层应该只探索输入图像中的局部区域,而不过度在意图像中相隔较远区域的关系,这就是"局部性"原则。最终,可以聚合这些局部特征,以在整个图像级别进行预测。
-
图像的平移不变性使我们以相同的方式处理局部图像,而不在乎它的位置。
-
局部性意味着计算相应的隐藏表示只需一小部分局部图像 像素。
-
在图像处理中,卷积层通常比全连接层需要更少的参数,但依旧获得高效用的模型。
-
卷积神经网络(CNN)是一类特殊的神经网络,它可以包含多个卷积层。
-
多个输入和输出通道使模型在每个空间位置可以获取图像的多方面特征。
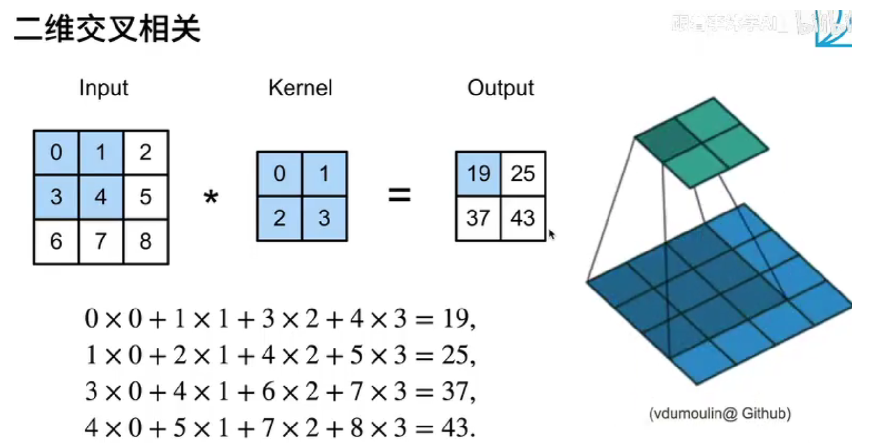
卷积层对输入和卷积核权重进行互相关运算,并在添加标量偏置之后产生输出。
所以,卷积层中的两个被训练的参数是卷积核权重W 和标量偏置b。就像我们之前随机初始化全连接层一样,在训练基于卷积层的模型时,我们也随机初始化卷积核权重。
|--------|--------------------------|-----------------|--------------|
| 维度 | 输入形状 (N,C,*spatial) | 典型库接口 | 例子 |
| 1D | (N, C, L) | nn.Conv1d | 文本、心电图、股票序列 |
| 2D | (N, C, H, W) | nn.Conv2d | 图像、特征图 |
| 3D | (N, C, D, H, W) | nn.Conv3d | 视频、CT/MRI 体素 |
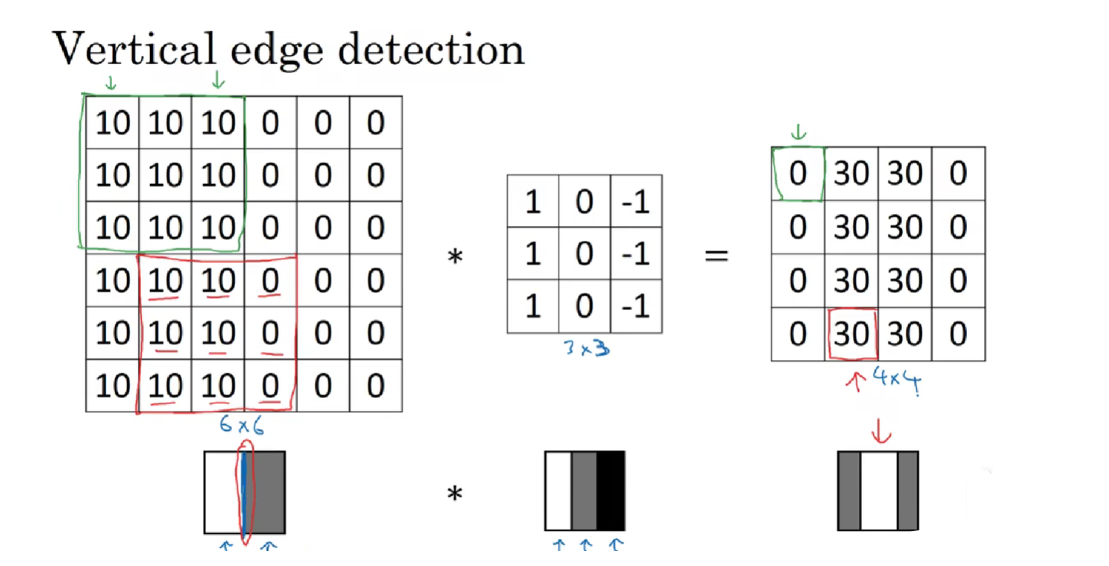
下图卷积后的结果中,中间的高亮区域表示边缘。
2. 自主实现卷积
2.1 自主实现卷积计算
import torch
from torch import nn
from d2l import torch as d2l
def corr2d(X, K): #@save
"""计算二维互相关运算"""
h, w = K.shape
Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
for i in range(Y.shape[0]):
for j in range(Y.shape[1]):
Y[i, j] = (X[i:i + h, j:j + w] * K).sum()
return Y
X = torch.tensor([[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]])
K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
corr2d(X, K)
结果为:
tensor([[19., 25.],
[37., 43.]])2.2 自主实现卷积层
class Conv2D(nn.Module):
def __init__(self, kernel_size):
super().__init__()
self.weight = nn.Parameter(torch.rand(kernel_size))
self.bias = nn.Parameter(torch.zeros(1))
def forward(self, x):
return corr2d(x, self.weight) + self.bias下面这个卷积核 K 只可以检测垂直边缘,无法检测水平边缘。
构建黑白图像X:
X = torch.ones((6, 8))
X[:, 2:6] = 0
构造一个高度为1、宽度为2的卷积核K:
K = torch.tensor([[1.0, -1.0]])
计算结果Y:【由X的(6,8)变为Y的(6,7)】
Y = corr2d(X, K)
Y
tensor([[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.]])怎么改进?
我们可以构造------可以学习的卷积核K!
3. 调库实现卷积操作
下面使用的是 nn 库的Conv2d函数,不是自主实现的,我们只是自主实现了训练过程:
# 构造一个二维卷积层,它具有1个输出通道和形状为(1,2)的卷积核
conv2d = nn.Conv2d(1,1, kernel_size=(1, 2), bias=False)
# 这个二维卷积层使用四维输入和输出格式(批量大小、通道、高度、宽度),
# 其中批量大小和通道数都为1
X = X.reshape((1, 1, 6, 8))
Y = Y.reshape((1, 1, 6, 7))
lr = 3e-2 # 学习率
for i in range(10):
Y_hat = conv2d(X)
l = (Y_hat - Y) ** 2 # 使用均方误差
conv2d.zero_grad()
l.sum().backward()
# 迭代卷积核
conv2d.weight.data[:] -= lr * conv2d.weight.grad
if (i + 1) % 2 == 0:
print(f'epoch {i+1}, loss {l.sum():.3f}')训练结果如下:
epoch 2, loss 6.422
epoch 4, loss 1.225
epoch 6, loss 0.266
epoch 8, loss 0.070
epoch 10, loss 0.022
查看参数:
conv2d.weight.data.reshape((1, 2))
参数结果如下,学习到的卷积核权重非常接近我们之前定义的卷积核K:
tensor([[ 1.0010, -0.9739]])下篇带来卷积神经网络操作中的填充和步幅。