题目：
利用矩阵求逆引理，证明（10.32）和（10.33）。提示：首先证明（10.33）然后利用它来证明（10.32）
解答：
由（10.28）和（10.29）得到了贝叶斯一般线性模型的均值和方差：
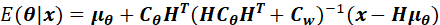
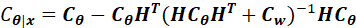
其中，线性关系满足：
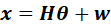
估计参数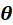
先验具有PDF~
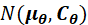，噪声
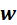与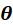
无关且PDF
.
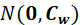上述两个均值和方差，存在另外一种形式，即（10.32）和（10.33）：
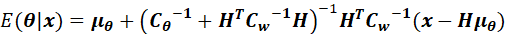
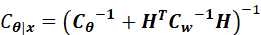
这两个公式转换，在（12.26）（12.27）也存在，因此证明非常有意义。
另外，对于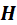
是列向量的情况，（10.33）计算也更加方便。
介绍矩阵求逆引理，即：
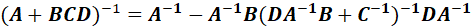
证明参考：
https://blog.csdn.net/yihaizhiyan/article/details/6084383
因此，套用上述公式，得到：
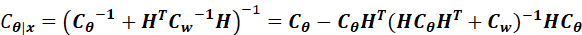
因此，（10.33）与（10.29）一致
接下来观察（10.32）中的：
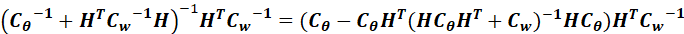
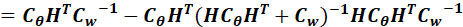
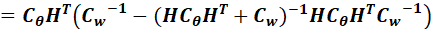
如果定义：
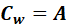
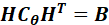
那么：
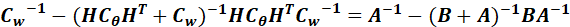
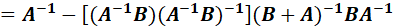
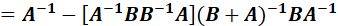
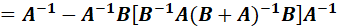
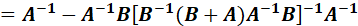
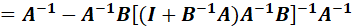
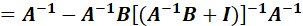
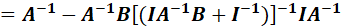
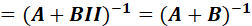
上面证明的最后第二步，又用了矩阵求逆引理，因此：
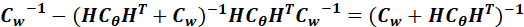
最终带入后，得到：
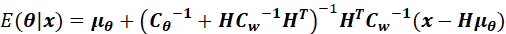
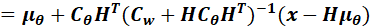
也就是10.32与10.28一致。