1.1 目标与范围
我们从简单的正弦函数开始,然后逐步过渡到更复杂的函数,以适应需要。
本章主要解释系统参数的物理意义,表明将水表面近似为正弦波的总和并不像人们通常认为的那样是随意的。我们特别关注将基本模型转换为实际实现所需的数学方法,因为这些数学方法是扩展实现的关键。
该系统适用于从小池塘到海洋的各种水体,从海湾或岛屿的角度进行观察。尽管这不是一个严格的物理模拟,但它确实能够提供令人信服、灵活且动态的水体渲染效果。由于该模拟完全在GPU上运行,因此不会与AI或物理争夺CPU资源。
由于系统参数具有一定的物理基础,因此它们比通过反复试验得出的参数更容易进行脚本编写。
将整个系统设置为动态的------除了其组件波浪之外------为系统增添了额外的生命力。
1.2 "正弦和"近似法
我们运行了两个表面模拟:一个是表面网格的几何起伏模拟,另一个是该网格上法线贴图中的涟漪模拟。这两个模拟本质上是相同的。水面的高度由简单周期波的总和来表示。我们从叠加正弦函数开始,随着进程发展,逐渐过渡到更有趣的波形。
正弦之和提供了一个连续函数,用于描述所有点上水面的高度和表面方向。在处理顶点时,我们根据每个顶点的水平位置对该函数进行采样,使网格符合其细分到连续水面的限制。在几何分辨率以下,我们将这种技术继续应用到纹理空间中。我们通过在渲染到渲染目标纹理的过程中,通过简单的像素着色器操作对正弦之和的近似法线进行采样,生成表面的法线贴图。每一帧渲染我们的法线贴图,让我们有限的正弦波集可以独立移动,极大地增强了渲染的真实感。
实际上,我们水体纹理中的细微波纹在很大程度上决定了我们模拟的真实感。我们波浪表面的几何波动为我们提供了一个更微妙的框架,用于呈现这种纹理。因此,我们对选择几何波浪还是纹理波浪有不同的标准。
1.2.1选择波形
我们需要一组参数来定义每个波形。如图1-2所示,这些参数包括:
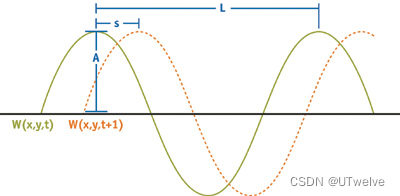
图1-2 单个波函数的参数
Wavelength 波长( L L L)
- 世界空间中波峰到波峰之间的距离。
- L L L 与频率 w w w 之间的关系为 w = 2 L w = \frac{2}{L} w=L2。
Amplitude 振幅( A A A)
- 从水平面到波峰的高度。
Speed 速度(S)
- 波峰每秒前进的距离。
- 将速度表示为相位常数 φ \varphi φ 更为方便。
- φ = S × 2 L \varphi = S \times \frac{2}{L} φ=S×L2
Direction 方向(D)
- 波前垂直方向上的水平向量,该向量指向波峰的运动方向。
然后,每个波的状态可以定义为水平位置 (x, y) 和时间 (t) 的函数:
Equation 1 公式1
W i ( x , y , t ) = A i × sin ( D i ⋅ ( x , y ) × w i + t × φ i ) W_{i}\left(x,y,t\right)= A_{i}\times\sin\left(\mathbf{D}{i} \cdot\left(x,y\right)\times w{i} + t\times\varphi_{i}\right) Wi(x,y,t)=Ai×sin(Di⋅(x,y)×wi+t×φi)
而整个表面是:
Equation 2 公式2
H ( x , y , t ) = ∑ ( A i × sin ( D i ⋅ ( x , y ) × w i + t × φ i ) ) H\left(x,y,t\right)=\sum\left(A_{i}\times\sin\left(\mathbf{D}{i} \cdot\left(x,y\right)\times w{i} + t\times\varphi_{i}\right)\right) H(x,y,t)=∑(Ai×sin(Di⋅(x,y)×wi+t×φi))
总和所有波的 i i i 。
为了在场景的动态中提供变化,我们将在一定的约束条件下随机生成这些波浪参数。随着时间的推移,我们将持续地将一个波浪渐隐,然后再以一组不同的参数将其渐显。事实证明,这些参数是相互依赖的。必须小心地为每个波浪生成一整套参数,这些参数需要以一种令人信服的方式组合在一起。
1.2.2 法线和切线
因为我们有一个关于表面的显式函数,我们可以直接计算任何给定点的表面方向,而不需要依赖有限差分技术。我们的副法线向量 B 和切线向量 T 是分别沿 x 和 y 方向的偏导数。对于二维水平面中的任何点 (x, y),表面上的三维位置 P 是:
Equation 3 公式3
P ( x , y , t ) = ( x , y , H ( x , y , t ) ) \mathbf{P}\begin{pmatrix}x,y,t\end{pmatrix}=\begin{pmatrix}x,y,H\begin{pmatrix}x,y,t\end{pmatrix}\end{pmatrix} P(x,y,t)=(x,y,H(x,y,t))
那么,x方向的偏导数是:
Equation 4a 公式4a
B ( x , y ) = ( ∂ x ∂ x , ∂ y ∂ x , ∂ ∂ x ( H ( x , y , t ) ) ) \mathbf{B}\left(x,y\right)=\left({\frac{\partial x}{\partial x}},{\frac{\partial y}{\partial x}},{\frac{\partial}{\partial x}}\left(H\left(x,y,t\right)\right)\right) B(x,y)=(∂x∂x,∂x∂y,∂x∂(H(x,y,t)))
Equation 4b 公式4b
B ( x , y ) = ( 1 , 0 , ∂ ∂ x ( H ( x , y , t ) ) ) \mathbf{B}\left(x,y\right)=\bigg(1,0,\frac{\partial}{\partial x}\big(H\left(x,y,t\right)\big)\bigg) B(x,y)=(1,0,∂x∂(H(x,y,t)))
同样地,切线向量为:
Equation 5a 公式5a
T ( x , y ) = ( ∂ x ∂ y , ∂ y ∂ y , ∂ ∂ y ( H ( x , y , t ) ) ) \mathbf{T}\left(x,y\right)=\left({\frac{\partial x}{\partial y}},{\frac{\partial y}{\partial y}},{\frac{\partial}{\partial y}}\left(H\left(x,y,t\right)\right)\right) T(x,y)=(∂y∂x,∂y∂y,∂y∂(H(x,y,t)))
Equation 5b 公式5b
T ( x , y ) = ( 0 , 1 , ∂ ∂ y ( H ( x , y , t ) ) ) \mathbf{T}\left(x,y\right)=\left(0,1,{\frac{\partial}{\partial y}}\left(H\left(x,y,t\right)\right)\right) T(x,y)=(0,1,∂y∂(H(x,y,t)))
法线由副法线和切线的叉积给出,表示为:
Equation 6a 公式6a
N ( x , y ) = B ( x , y ) × T ( x , y ) \mathbf{N}(x,y)=\mathbf{B}(x,y)\times\mathbf{T}(x,y) N(x,y)=B(x,y)×T(x,y)
Equation 6b 公式6b
N ( x , y ) = ( − ∂ ∂ x ( H ( x , y , t ) ) , − ∂ ∂ y ( H ( x , y , t ) ) , 1 ) \mathbf{N}\left(x,y\right)=\left(-\frac{\partial}{\partial x}\Big(H\left(x,y,t\right)\Big),-\frac{\partial}{\partial y}\Big(H\left(x,y,t\right)\Big),1\right) N(x,y)=(−∂x∂(H(x,y,t)),−∂y∂(H(x,y,t)),1)
在我们将函数 H H H 的偏导数代入之前,请注意方程 3-6 中的公式是多么方便。两个偏导数的计算为我们提供了切空间基的九个分量。这是我们使用高度场来近似我们表面的直接后果。
即 P ( x , y ) . x = x P(x, y).x = x P(x,y).x=x 和 P ( x , y ) . y = y P(x, y).y = y P(x,y).y=y ,在偏导数中变成了0和1。这仅适用于这样的高度场,但对我们选择的任何函数 H ( x , y , t ) H(x, y, t) H(x,y,t) 都是通用的。
对于 选择波形 章节中描述的高度函数,其偏导数特别容易计算。因为函数的导数是各部分导数之和:
Equation 7 公式7
∂ ∂ x ( H ( x , y , t ) ) = ∑ ( ∂ ∂ x ( W i ( x , y , t ) ) ) = ∑ ( w i × D i . x × A i × cos ( D i ⋅ ( x , y ) × w i + t × φ i ) ) \begin{aligned} {\frac{\partial}{\partial x}}\big(H(x,y,t)\big)& =\sum\biggl(\frac{\partial}{\partial x}\bigl(W_{i}\bigl(x,y,t\bigr)\bigr)\biggr) \\ &=\sum\left(w_{i}\times\mathbf{D}{i}.x\times A{i}\times\cos\left(\mathbf{D}{i}\cdot(x,y)\times w{i}+t\times\varphi_{i}\right)\right) \end{aligned} ∂x∂(H(x,y,t))=∑(∂x∂(Wi(x,y,t)))=∑(wi×Di.x×Ai×cos(Di⋅(x,y)×wi+t×φi))
覆盖所有波浪 i i i 。
关于通过直接叠加正弦波生成的波浪的一个常见抱怨是它们有太多的"滚动",而真实的波浪拥有更尖锐的峰和更宽的谷。事实证明,有一个简单的正弦函数变体可以非常可控地产生这种效果。我们将我们的正弦函数偏移使其非负,并将其提高到指数 k。该函数及其相对于 x 的偏导数是:
Equation 8a 公式8a
W i ( x , y , t ) = 2 A i × ( sin ( D i ⋅ ( x , y ) × w i + t × φ i ) + 1 2 ) k W_{i}\left(x,y,t\right)=2A_{i}\times\left(\frac{\sin\left(\mathbf{D}{i}\cdot\left(x,y\right)\times w{i}+t\times\varphi_{i}\right)+1}{2}\right)^{k} Wi(x,y,t)=2Ai×(2sin(Di⋅(x,y)×wi+t×φi)+1)k
Equation 8b 公式8b
∂ ∂ x ( W i ( x , y , t ) ) = k × D i . x × w i × A i × ( sin ( D i ⋅ ( x , y ) × w i + t × φ i ) + 1 2 ) k − 1 × cos ( D i ⋅ ( x , y ) × w i + t × φ i ) . \begin{aligned}\frac{\partial}{\partial x}\big(W_{i}\left(x,y,t\right)\big)&=k\times\mathbf{D}{i}.x\times w{i}\times A_{i}\times\left(\frac{\sin\left(\mathbf{D}{i}\cdot\left(x,y\right)\times w{i}+t\times\varphi_{i}\right)+1}{2}\right)^{k-1}\\&\quad\times\cos\left(\mathbf{D}{i}\cdot\left(x,y\right)\times w{i}+t\times\varphi_{i}\right).\end{aligned} ∂x∂(Wi(x,y,t))=k×Di.x×wi×Ai×(2sin(Di⋅(x,y)×wi+t×φi)+1)k−1×cos(Di⋅(x,y)×wi+t×φi).
图 1-3 展示了作为功率常数 k 的函数生成的波形。这是我们实际用于纹理波的函数,但为了简化,我们继续用我们简单的正弦和来表达波浪,并且我们注意到我们必须在何处考虑我们在基础波形中的变化。
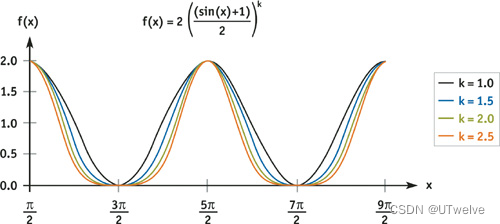
图1-3 不同波形的示例
1.2.3 几何波形GeometricWaves
我们将自己限制在四种几何波形中。增加更多的波形并不涉及新概念,只是增加了更多相同的顶点着色器指令和常数。
方向性或圆形DirectionalOrCircular
我们可以选择圆形或方向性波形,如图1-4所示。方向性波形需要的顶点着色器指令稍微少一些,但具体选择取决于正在模拟的场景。
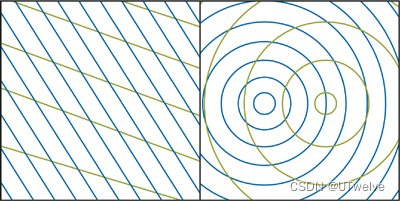
图1-4 方向波与环形波
对于方向性波浪,方程1中的每一个 D i D_i Di 在波浪的整个生命周期内都是常数。
对于圆形波浪,方向必须在每个顶点处计算,简单来说就是从波浪中心 C i C_i Ci 到顶点的规范化向量:
D i ( x , y ) = ( ( x , y ) − C i ∣ ( x , y ) − C i ∣ ) \mathbf{D}{i}\left(x,y\right)=\left({\frac{\left(x,y\right)-\mathbf{C}{i}}{\left|\left(x,y\right)-\mathbf{C}_{i}\right|}}\right) Di(x,y)=(∣(x,y)−Ci∣(x,y)−Ci)
对于大面积的水体,方向性波浪通常更受青睐,因为它们更好地模拟了风驱动的波浪。对于波浪来源不是风的小型水池(如瀑布底部),圆形波浪更为合适。圆形波浪还有一个好处是它们的干涉图案永不重复。
这两种类型的波浪的实现非常相似。
对于方向性波浪,波浪方向是从关于风向的某个范围内随机抽取的。
对于圆形波浪,波浪中心是从某个有限范围内随机抽取的(例如瀑布击中水面的线)。
接下来的讨论将重点放在方向性波浪上。
格斯特纳波GerstnerWaves
为了有效的模拟,我们需要控制波浪的陡峭程度。如前所述,正弦波呈现出圆润的外观------这可能正是我们想要的平静、田园诗般的池塘效果。但对于粗糙的海面,我们需要形成更尖锐的波峰和更宽阔的波谷。我们可以使用公式8a和8b来实现所需的形状,但我们选择了相关的格斯特纳波。格斯特纳波函数最初是在计算机图形学出现很久之前就被开发出来,用于在物理基础上模拟海水。因此,格斯特纳波提供了一些表面运动的微妙变化,这些变化非常令人信服而不显突兀。(详细描述参见Tessendorf 2001)。
我们选择格斯特纳波,因为它们有一个常被忽视的特性:通过将顶点向每个波峰移动,它们形成了更尖锐的波峰。由于波峰是表面上最尖锐(即最高频)的特征,这正是我们希望顶点集中的地方,如图1-5所示。
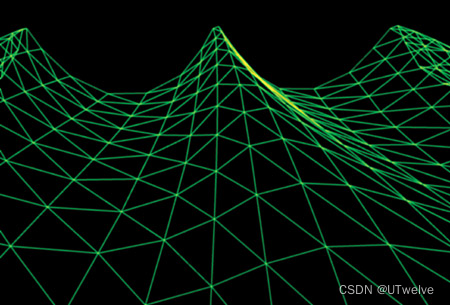
图1-5 GerstnerWaves
这是GerstnerWaves函数:
Equation 9 公式9
P ( x , y , t ) = ( x + ∑ ( Q i A i × D i . x × cos ( w i D i ⋅ ( x , y ) + φ i t ) ) , y + ∑ ( Q i A i × D i . y × cos ( w i D i ⋅ ( x , y ) + φ i t ) ) , ∑ ( A i sin ( w i D i ⋅ ( x , y ) + φ i t ) ) , ) \mathbf{P}\left(x,y,t\right)=\left(\begin{array}{l}{{x+\sum\left(Q_{i}A_{i}\times\mathbf{D}{i}.x\times\cos\left(w{i}\mathbf{D}{i} \cdot\left(x,y\right)+\varphi{i}t\right)\right),}}\\{{y+\sum\left(Q_{i}A_{i}\times\mathbf{D}{i}.y\times\cos\left(w{i}\mathbf{D}{i} \cdot\left(x,y\right)+\varphi{i}t\right)\right),}}\\{{\sum\left(A_{i}\sin\left(w_{i}\mathbf{D}{i} \cdot\left(x,y\right)+\varphi{i}t\right)\right),}}\end{array}\right) P(x,y,t)= x+∑(QiAi×Di.x×cos(wiDi⋅(x,y)+φit)),y+∑(QiAi×Di.y×cos(wiDi⋅(x,y)+φit)),∑(Aisin(wiDi⋅(x,y)+φit)),
这里 Q i Q_i Qi 是一个控制波浪陡峭程度的参数。
对于单个波浪 i i i, Q i = 0 Q_i=0 Qi=0 产生常见的滚动正弦波,而 Q i = 1 w i A i Q_i = \frac{1}{w_i A_i} Qi=wiAi1 产生尖锐的波峰。应避免使用较大的 Q i Q_i Qi 值,因为它们会在波峰上方形成环。
实际上,我们可以将 Q Q Q 作为"陡峭程度"参数留给制作艺术家来指定,允许范围是 0 0 0 到 1 1 1,并使用 Q i = Q w i A i × numWaves Q_i = \frac{Q}{w_i A_i \times \text{numWaves}} Qi=wiAi×numWavesQ 来变化,从完全平滑的波浪到我们能产生的最尖锐的波浪。
值得注意的是,公式3和公式9之间唯一的区别是顶点的侧向移动。高度是相同的。这意味着我们不再有一个严格的高度函数。即, P ( x , y , t ) . x ≠ x \mathbf{P}(x,y,t).x \neq x P(x,y,t).x=x 然而,该函数仍然容易微分,并且有一些方便的项消去。为了省去推导过程,作为读者的练习,我们看到切向空间基向量是:
Equation 10 公式10
B = ( 1 − ∑ ( Q i × D i . x 2 × W A × S ( ) ) , − ∑ ( Q i × D i . x × D i . y × W A × S ( ) ) , ∑ ( D i . x × W A × C ( ) ) ) \mathbf{B}= \begin{pmatrix} 1-\sum\bigl(Q_{i}\times\mathbf{D}{i}.x^{2}\times WA\times S()\bigr),\\ -\sum\bigl(Q{i}\times\mathbf{D}{i}.x\times\mathbf{D}{i}.y\times WA\times S()\bigr),\\ \sum\bigl(\mathbf{D}_{i}.x\times WA\times C()\bigr) \end{pmatrix} B= 1−∑(Qi×Di.x2×WA×S()),−∑(Qi×Di.x×Di.y×WA×S()),∑(Di.x×WA×C())
Equation 11 公式11
T = ( − ∑ ( Q i × D i . x × D i . y × W A × S ( ) ) , 1 − ∑ ( Q i × D i . y 2 × W A × S ( ) ) , ∑ ( D i . y × W A × C ( ) ) ) \mathbf{T}= \begin{pmatrix} -\sum\bigl(Q_{i}\times\mathbf{D}{i}.x\times\mathbf{D}{i}.y\times WA\times S()\bigr),\\ 1-\sum\bigl(Q_{i}\times\mathbf{D}{i}.y^{2}\times WA\times S()\bigr),\\ \sum\bigl(\mathbf{D}{i}.y\times WA\times C()\bigr) \end{pmatrix} T= −∑(Qi×Di.x×Di.y×WA×S()),1−∑(Qi×Di.y2×WA×S()),∑(Di.y×WA×C())
Equation 12 公式12
N = ( − ∑ ( D i . x × W A × C ( ) ) , − ∑ ( D i . y × W A × C ( ) ) , ∑ ( Q i × W A × S ( ) ) ) \mathbf{N}= \begin{pmatrix} -\sum\bigl(\mathbf{D}{i}.x\times WA\times C()\bigr),\\ -\sum\bigl(\mathbf{D}{i}.y\times WA\times C()\bigr),\\ \sum\bigl(Q_{i}\times WA\times S()\bigr) \end{pmatrix} N= −∑(Di.x×WA×C()),−∑(Di.y×WA×C()),∑(Qi×WA×S())
说明:
W A = w i × A i , WA=w_{i}\times A_{i}, WA=wi×Ai,
S ( ) = sin ( w i × D i ⋅ P + φ i t ) S()=\sin\left(w_{i}\times\mathbf{D}{i}\cdot\mathbf{P}+\varphi{i}t\right) S()=sin(wi×Di⋅P+φit)
C ( ) = cos ( w i × D i ⋅ P + φ i t ) C()=\cos\bigl(w_{i}\times\mathbf{D}{i}\cdot\mathbf{P}+\varphi{i}t\bigr) C()=cos(wi×Di⋅P+φit)
这些公式不像4b、5b和6b方程那样简洁明了,但它们计算起来非常高效。
在形成波峰环的背景下,仔细观察法线的 z z z 分量证明了这一点非常有趣。虽然 Tessendorf (2001) 从流体动力学的纳维-斯托克斯[1](#1)描述和"李变换技术[2](#2)"中推导出他的"切碎效应[3](#3)",最终结果是在频率域中表达的格斯特纳波的一个变体。
在频率域中,可以避免并检测到波顶的环形,但在空间域中,我们可以清楚地看到正在发生的事情。
当 Q i × w i × A i Q_i \times w_i \times A_i Qi×wi×Ai 的和大于 1 1 1 时,我们法线的 z z z 分量在峰值处可能变为负值,因为我们的波浪会在自身上方形成环。
只要我们选择的 Q i Q_i Qi 使得这个和始终小于或等于 1 1 1,我们将形成尖锐的峰值但永远不会形成环。
1.2.4参数解释
波长和速度 Wavelength Speed
我们首先选择合适的波长。与其追求现实世界的分布,不如最大化我们能承担的少数波浪的效果。
相似长度的波浪的叠加突出了水面的动态性。
因此,我们选择一个中值波长,并在该长度的一半到两倍之间生成随机波长。中值波长在创作过程中被编写,它可以随时间变化。
例如,在暴风雨期间,波浪可能比晴朗平静时显著更大。
注意,我们不能改变活跃波浪的波长。即便是逐渐改变,波浪的波峰也会向原点扩展或收缩,这看起来非常不自然。因此,我们改变当前的平均波长,随着时间的推移,当波浪逐渐消退,它们将基于新的长度重新生成。方向也是如此。
根据波长,我们可以轻松计算它在表面上的传播速度。水的色散关系(参见 Tessendorf 2001),忽略高阶项,给出:
Equation 13 公式13
w = g × 2 π L w=\sqrt{g\times{\frac{2\pi}{L}}} w=g×L2π
其中 w w w 是频率, g g g 是我们使用的单位(例如 9.8 m/s²)下的重力常数, L L L 是波峰到波峰的长度。
振幅 Amplitude
如何处理振幅是一个见仁见智的问题。
虽然可能存在关于波浪振幅作为波长和当前天气条件的函数的推导,但我们使用在创作时指定的常数(或脚本化的)比率。
更准确地说,与中值波长一起,艺术家指定了一个中值振幅。
对于任何大小的波浪,其振幅与波长的比率将匹配中值振幅与中值波长的比率。
方向 Direction
波浪行进的方向与其他参数完全独立,因此我们可以根据自己选择的任何标准为每个波浪选择一个方向。
如前所述,我们从大致是风向的恒定向量开始。然后我们从风向的恒定角度内随机选择方向。
这个恒定角度在内容创建时被指定,或者可能被脚本化。
- 参考来自Gerstner Waves圣经------ Mark Finch - Cyan Worlds GPU Gems