【模板】树状数组 1
题目描述
如题,已知一个数列,你需要进行下面两种操作:
-
将某一个数加上 x x x
-
求出某区间每一个数的和
输入格式
第一行包含两个正整数 n , m n,m n,m,分别表示该数列数字的个数和操作的总个数。
第二行包含 n n n 个用空格分隔的整数,其中第 i i i 个数字表示数列第 i i i 项的初始值。
接下来 m m m 行每行包含 3 3 3 个整数,表示一个操作,具体如下:
-
1 x k含义:将第 x x x 个数加上 k k k -
2 x y含义:输出区间 [ x , y ] [x,y] [x,y] 内每个数的和
输出格式
输出包含若干行整数,即为所有操作 2 2 2 的结果。
样例 #1
样例输入 #1
5 5
1 5 4 2 3
1 1 3
2 2 5
1 3 -1
1 4 2
2 1 4样例输出 #1
14
16提示
【数据范围】
对于 30 % 30\% 30% 的数据, 1 ≤ n ≤ 8 1 \le n \le 8 1≤n≤8, 1 ≤ m ≤ 10 1\le m \le 10 1≤m≤10;
对于 70 % 70\% 70% 的数据, 1 ≤ n , m ≤ 1 0 4 1\le n,m \le 10^4 1≤n,m≤104;
对于 100 % 100\% 100% 的数据, 1 ≤ n , m ≤ 5 × 1 0 5 1\le n,m \le 5\times 10^5 1≤n,m≤5×105。
数据保证对于任意时刻, a a a 的任意子区间(包括长度为 1 1 1 和 n n n 的子区间)和均在 [ − 2 31 , 2 31 ) [-2^{31}, 2^{31}) [−231,231) 范围内。
样例说明:
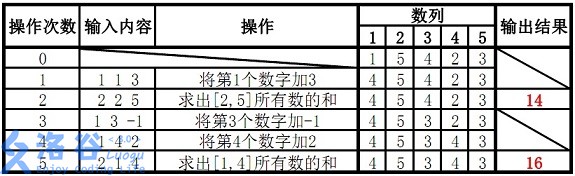
故输出结果14、16
树状数组
树状数组(Binary Indexed Tree,简称 BIT)是一种用于高效处理频繁更新和前缀和查询的数据结构。它能够在 O(logn) 时间复杂度内完成更新和查询操作,因此在处理需要频繁动态更新的数据时非常有用。
经典树状数组主要用于解决以下两类问题:
单点更新问题:对数组中的某个元素进行更新(加一个值或改为一个新值)。
前缀和问题:求数组中从第一个元素到某个位置的前缀和。
树状数组的原理
树状数组存储的信息
假设arr数组有九个元素,tree数组同样有九个元素,这九个元素的下标从1开始计算.

tree数组下标1存储arr数组中下标1累加和.
tree数组下标2存储arr数组中下标1,2累加和.
tree数组下标3存储arr数组中下标3累加和.
tree数组下标4存储arr数组中下标1,2,3,4累加和.
tree数组下标5存储arr数组中下标5累加和.
tree数组下标6存储arr数组中下标5,6累加和.
tree数组下标7存储arr数组中下标7累加和.
tree数组下标8存储arr数组中下标1,2,3,4,5,6,7,8累加和.
tree数组下标9存储arr数组中下标9累加和.
树状数组存储信息的理解

在右边画出1,2,3,4,5,6,7,8,9.
tree数组下标1存储arr数组下标1的累加和.在右边1下面画一条长度为1的线.
tree数组下标2存储arr数组中下标1,2累加和.在右边2下面画一条长度为1的线,前面线长度为1和自己的长度相同,那么两者合并成长度为2的线.表示1,2累加和.
tree数组下标3存储arr数组中下标3累加和.在右边3下面画一条长度为1的线,前面线的长度为2,和自己的长度不相同,不能合并.
tree数组下标4存储arr数组中下标1,2,3,4累加和.在右边4下面画一条长度为1的线,前面线的长度为1,和自己的长度相同,合并在一起得到长度为2的线,对应34位置,前面线的长度为2,和自己的长度相同,合并在一起得到长度为4的线,表示1,2,3,4累加和.
tree数组下标5存储arr数组中下标5累加和.在右边5下面画一条长度为1的线,前面线的长度是4,和自己不相同,不能合并.
tree数组下标6存储arr数组中下标5,6累加和.在右边6下面画一条长度为1的线,前面线的长度是1,和自己相同,合并成长度为2的线,前面线的长度为4,和自己不相同,不能合并.
tree数组下标7存储arr数组中下标7累加和.在右边7下面画上一条长度为1的线,前面线的长度为2,和自己不相同不能合并.
tree数组下标8存储arr数组中下标1,2,3,4,5,6,7,8累加和.,在右边8下面画一条长度为1的线,前面线的长度为1,和自己相同,合并在一起长度为2,前面线的长度为2,和自己相同,合并在一起长度为4,前面线的长度为4,和自己相同,合并在一起长度为8,表示1,2,3,4,5,6,7,8累加和.
tree数组下标9存储arr数组中下标9累加和.在右边9下面画一条长度为1的线,前面线的长度为8,和自己不相同,不能合并.
lowbit(int i)函数
cpp
lowbit(int i){
return i&(-i);
}lowbit 函数在树状数组(Binary Indexed Tree, BIT)中扮演着关键角色,主要用于确定如何在更新和查询操作中跳转节点。lowbit 函数的作用是获取一个数的最低位的1所表示的值。
具体来说,lowbit(x) 返回的是 x 的二进制表示中最低位的1所在的位置所表示的值。在二进制中,最低位的1表示的值是 x & -x。
在二进制中-x是通过对x的二进制按位取反,末尾加一得到.

对于任意的x,x&(-x)的结果是只保留x在二进制中最低位的1,其余的数全是0.
add(int i,int v) 函数
cpp
void add(int i, int v) {
while (i <= n) {
tree[i] += v;
i += lowbit(i);
}
}该函数的意思是将arr数组中i位置的值加上v.

我们只处理tree数组中的数据,假设我们调用add(5,3),将arr[5]+=3.
那么我们需要将tree数组中下标为5,6,8位置的元素全部加上3.表示这些位置中含有的下标5的值增加3.
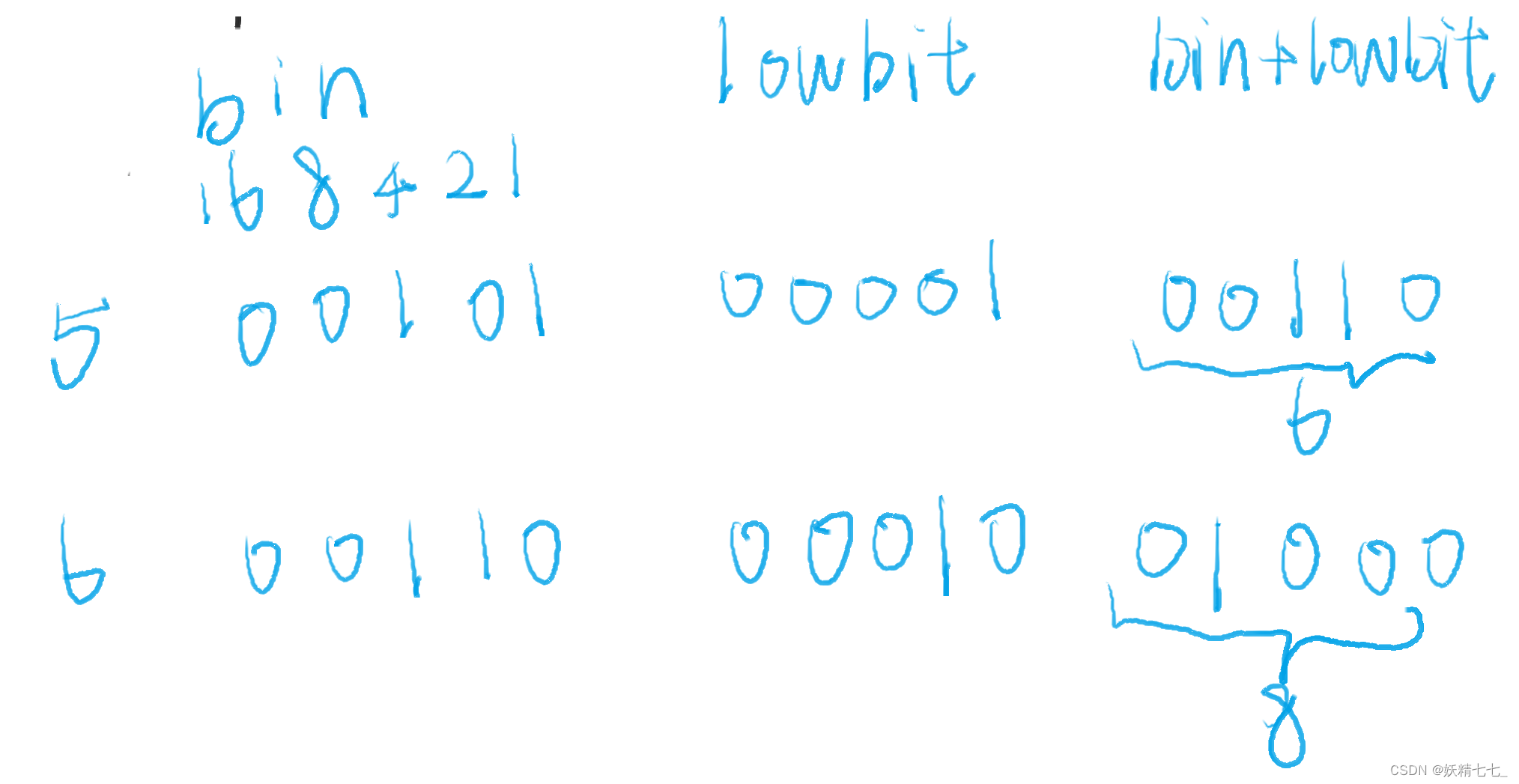
我们研究其二进制数可以发现,数字5的二进制数加上lowbit(5)得到的数是6,数字6的二进制数加上lowbit(6)得到的数是8.

假设我们再调用add(4,3),将arr[4]+=3.
那么我们需要将tree数组中4,8下标位置的元素全部加上3,表示这些位置中含有的下标4的值增加3.
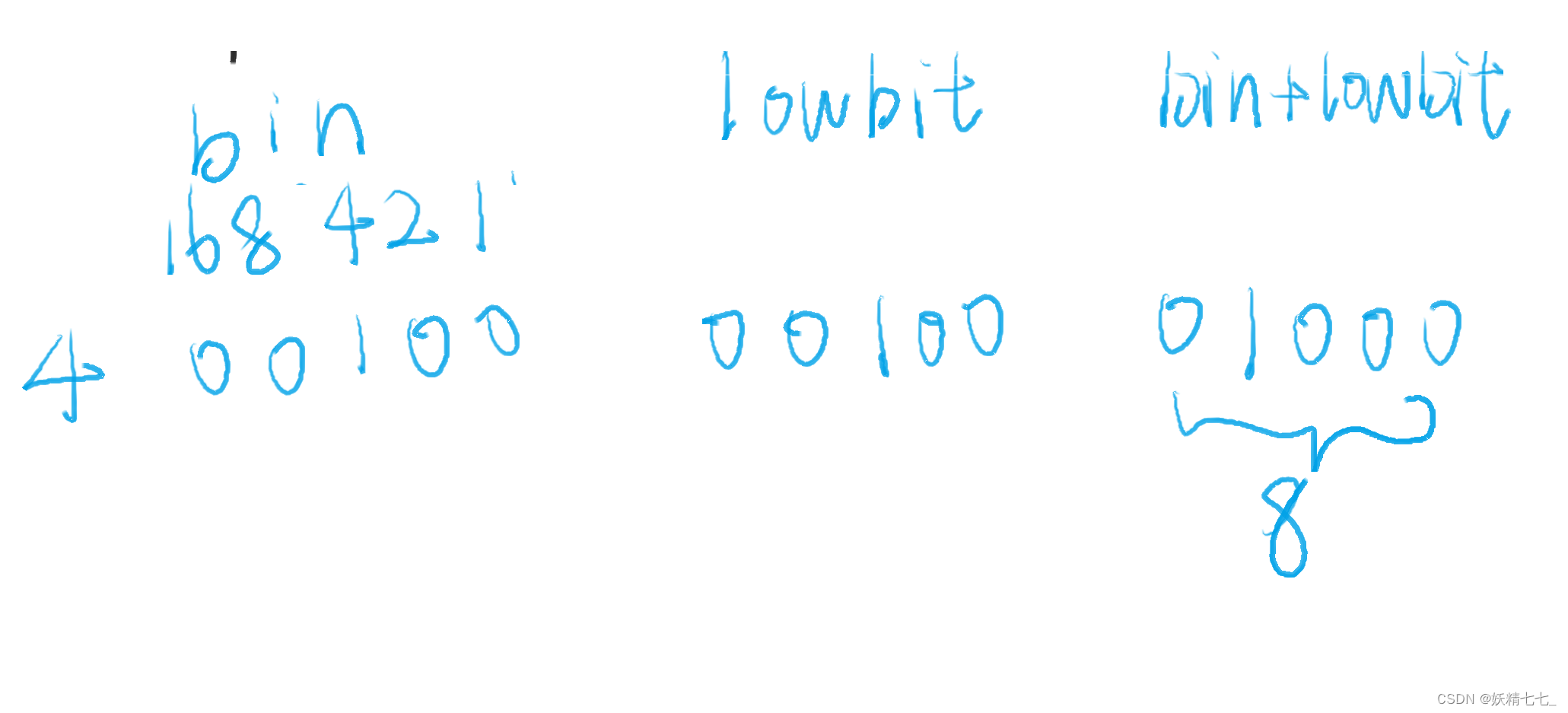
我们研究其二进制数可以发现,数字4的二进制数加上lowbit(4)得到的数是8.
实际上对于arr数组中任意的i位置我们增加v,对应tree数组中需要修改的位置是i,i+lowbit(i)=newi,newi+lowbit(newi)...直到越界为止.
sum(int i)函数
cpp
int sum(int i) {
int ret = 0;
while (i > 0) {
ret += tree[i];
i -= lowbit(i);
}
return ret;
}sum 函数在树状数组(Binary Indexed Tree, BIT)中通常用于计算数组的前缀和,即从数组开头到某个位置的元素总和。这个操作在 BIT 中能够以对数时间复杂度 O(logn) 来完成。
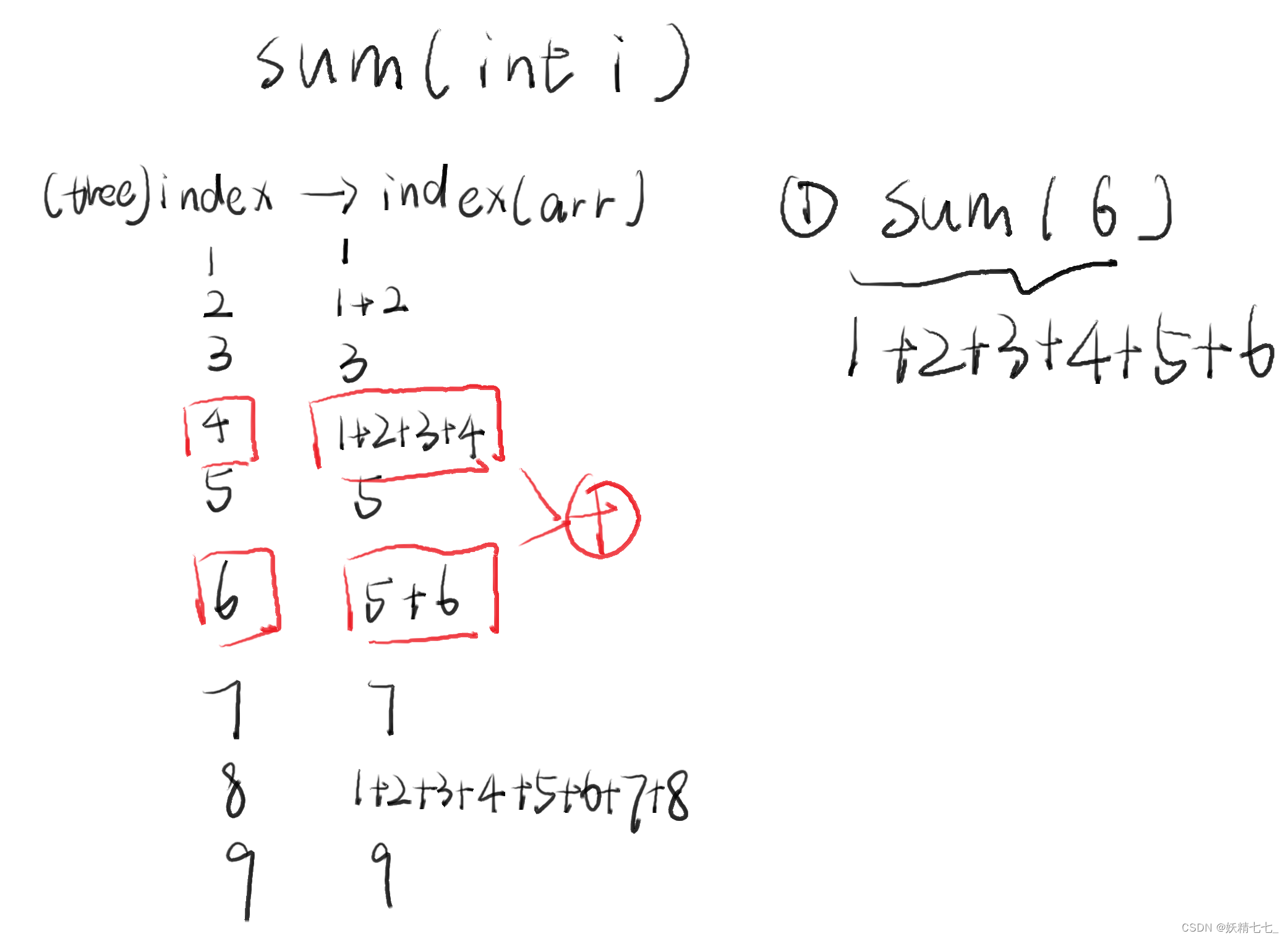
假设我们需要求arr数组中1~6前缀和,对应tree数组中需要得到下标4,6的累加和.
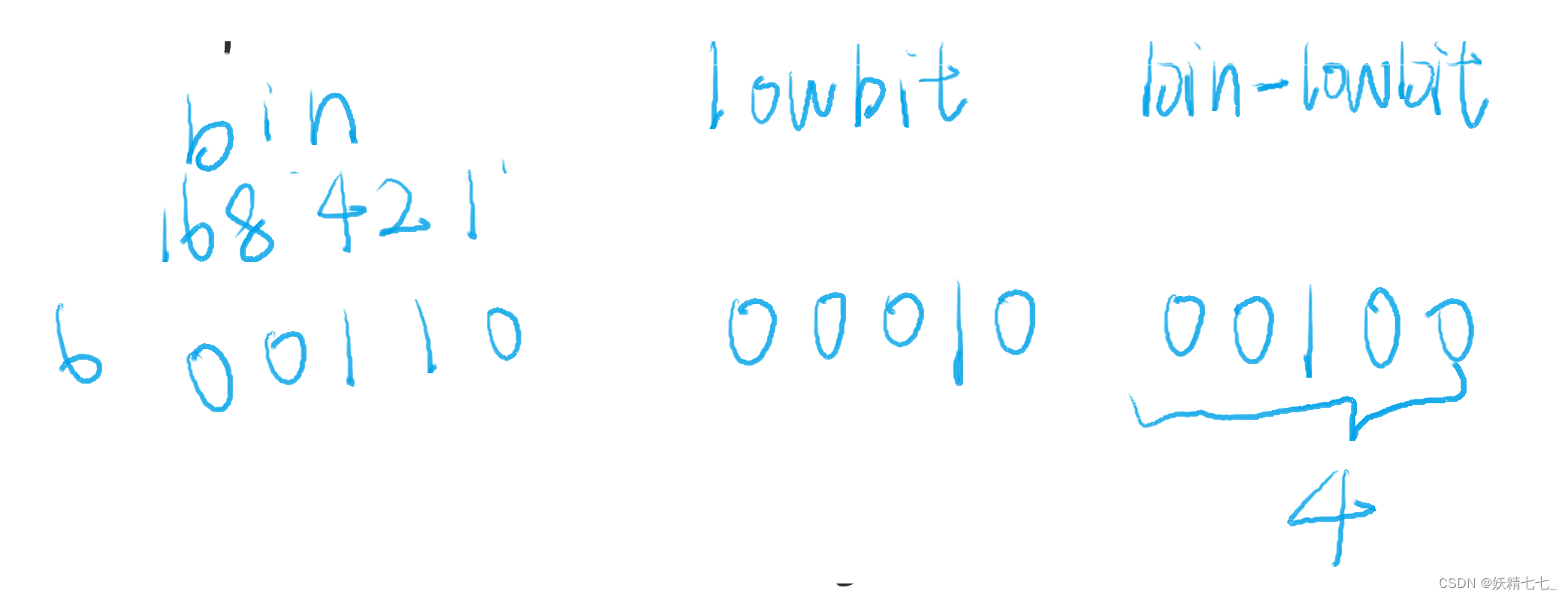
研究其二进制关系,发现6的二进制数减去lowbit(6)得到的数是4.

假设我们需要求arr数组中1~7前缀和,对应tree数组中需要得到下标4,6,7累加和.
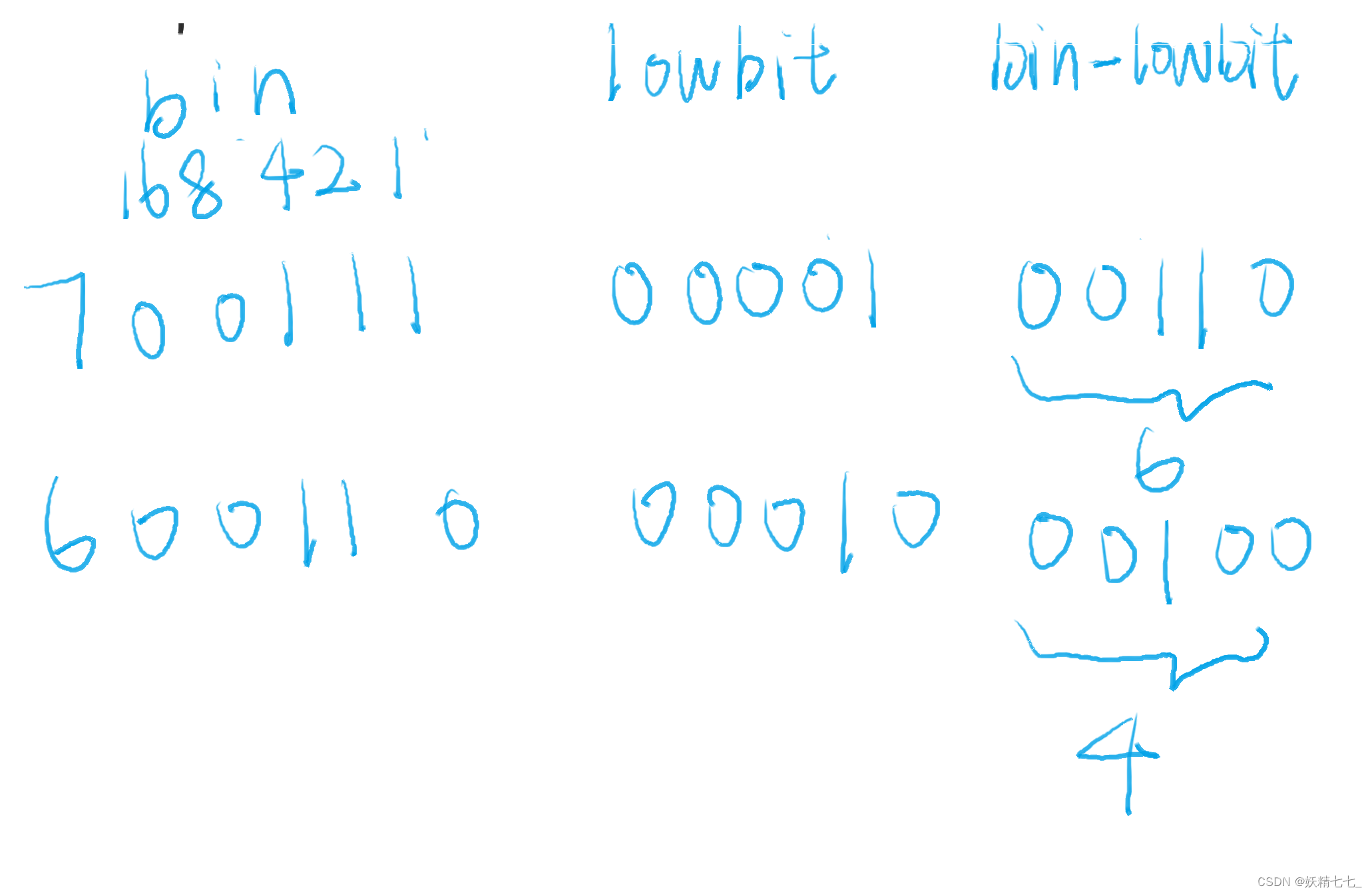
研究其二进制数关系发现,7的二进制数减去lowbit(7)得到的数是6.
6的二进制数减去lowbit(6)得到的数是4.
实际上我们需要求arr数组中1~x的前缀和,对应tree数组中需要累加的下标位置分别是,x,x-lowbit(x)=newx,newx-lowbit(newx)...直到遇到下标0为止.
range(int l,int r)
cpp
int range(int l, int r) {
return sum(r) - sum(l - 1);
}range函数计算arr数组中区间和,区间和用前缀和加工得到.
完整代码
cpp
#include<bits/stdc++.h> // 引入标准库
using namespace std;
#define int long long // 定义长整型为int
#define endl '\n' // 定义换行符
int n, m; // n表示数列长度,m表示操作的总个数
vector<int> arr; // 存储数列的数组
vector<int> diff; // 存储差分数组
struct node {
int op, x, y, k; // op表示操作类型,x和y表示操作的参数,k表示增加的值
};
vector<node> readd; // 存储所有操作的数组
class Tree { // 树状数组类
public:
vector<int> tree; // 树状数组
// 计算lowbit
int lowbit(int i) {
return i & -i;
}
// 在树状数组中增加值
void add(int i, int k) {
while (i <= n) {
tree[i] += k;
i += lowbit(i);
}
}
// 计算前缀和
int sum(int i) {
int ret = 0;
while (i > 0) {
ret += tree[i];
i -= lowbit(i);
}
return ret;
}
// 计算区间和
int range(int l, int r) {
return sum(r) - sum(l - 1);
}
// 构造函数,用于初始化树状数组
Tree(vector<int> arr) {
tree.assign(arr.size(), 0); // 初始化树状数组
for (int i = 1; i < arr.size(); i++) {
add(i, arr[i]); // 初始化时将数组中的值加入树状数组
}
}
Tree() {} // 默认构造函数
};
Tree t1; // 定义树状数组对象
void init() { // 初始化函数
cin >> n >> m; // 读取数列长度和操作个数
arr.assign(n + 5, 0); // 初始化数组,大小为n+5
readd.clear(); // 清空操作数组
for (int i = 1; i <= n; i++) {
cin >> arr[i]; // 读取数列初始值
}
for (int i = 1; i <= m; i++) {
int op = 0, x = 0, y = 0, k = 0;
cin >> op; // 读取操作类型
if (op == 1) {
cin >> x >> y >> k; // 读取区间增加操作的参数
} else {
cin >> x; // 读取查询操作的参数
}
readd.push_back({ op, x, y, k }); // 将操作存储到操作数组中
}
}
void solve() {
diff.assign(arr.size(), 0); // 初始化差分数组
for (int i = 1; i < arr.size(); i++) {
diff[i] = arr[i] - arr[i - 1]; // 计算差分数组
}
t1 = Tree(diff); // 初始化树状数组
for (auto& xx : readd) { // 遍历所有操作
int op = xx.op, x = xx.x, y = xx.y, k = xx.k;
if (op == 1) { // 如果是增加操作
t1.add(x, k); // 在x位置增加k
t1.add(y + 1, -k); // 在y+1位置减少k
} else { // 如果是查询操作
cout << t1.sum(x) << endl; // 输出第x个数的值
}
}
}
signed main() {
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); // 提高输入输出效率
init(); // 初始化
solve(); // 处理所有操作
}并查集
描述
给定一个没有重复值的整形数组arr,初始时认为arr中每一个数各自都是一个单独的集合。请设计一种叫UnionFind的结构,并提供以下两个操作。
boolean isSameSet(int a, int b): 查询a和b这两个数是否属于一个集合
void union(int a,int b): 把a所在的集合与b所在的集合合并在一起,原本两个集合各自的元素以后都算作同一个集合
要求
如果调用isSameSet和union的总次数逼近或超过O(N),请做到单次调用isSameSet或union方法的平均时间复杂度为O(1)
输入描述: 第一行两个整数N, M。分别表示数组大小、操作次数 接下来M行,每行有一个整数opt
若opt = 1,后面有两个数x,y,表示查询(x, y)这两个数是否属于同一个集合
若opt = 2,后面有两个数x, y,表示把x, y所在的集合合并在一起 输出描述:
对于每个opt = 1的操作,若为真则输出"Yes",否则输出"No"
示例1 输入: 4 5 1 1 2 2 2 3 2 1 3 1 1
1 1 2 3 复制
输出: No Yes Yes 复制
说明: 每次2操作后的集合为 ({1}, {2}, {3}, {4}) ({1}, {2, 3}, {4}) ({1, 2, 3}, {4})
备注: 1 \leqslant N, M \leqslant
10^61⩽N,M⩽10 6 保证1 \leqslant x, y \leqslant N保证1⩽x,y⩽N
并查集(Disjoint Set Union, DSU)是一种用于处理不相交集合的数据结构,支持高效的合并(union)和查找(find)操作。find 函数在并查集中用于查找元素所属的集合代表(即根节点)。为了提高查找效率,find 函数通常结合路径压缩(path compression)技术使用。
并查集原理
father数组存储的信息

一开始元素1,2,3,4都是自己和自己一个集合.
index下标表示的是每一个元素,father元素值表示的元素的父亲节点元素.
一开始所有的元素的父亲节点都是自己.
代表节点
如果一个元素的父亲节点是自己,那么这个节点就是代表节点,也叫做代表元素,此时这个元素表示的就是一个集合.
find(int i)函数
cpp
int findd(int i) { // 查找操作,带路径压缩
if (father[i] != i) father[i] = findd(father[i]); // 如果 i 不是自己的父节点,递归查找父节点
return father[i]; // 返回父节点
}find 函数用于找到某个元素所属集合的根节点.

find(4),判断4是不是代表元素,4指向的不是自己,不是代表元素,那么就往上面走,4指向3,判断3是不是代表元素,3指向的不是自己,不是代表元素,继续往上走,3指向2,判断2是不是代表元素,2指向的不是自己,不是代表元素,继续往上走,2指向1,判断1是不是代表元素,1是代表元素,所以4所在的集合是1所在集合的集合.
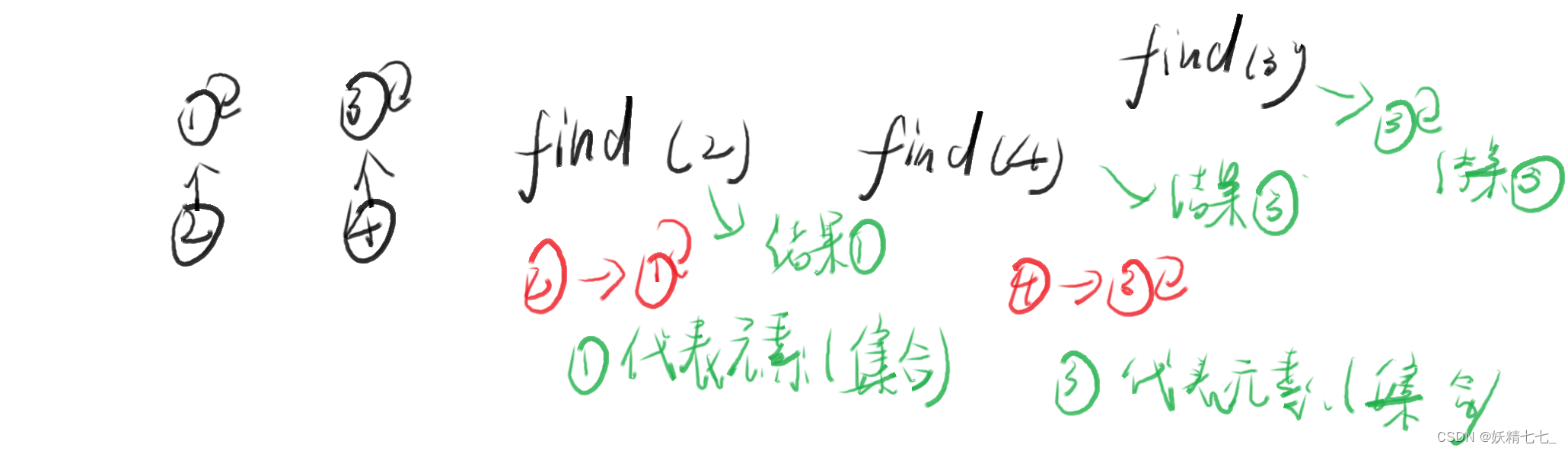
find(2),判断2是不是代表元素,2指向的不是自己,不是代表元素,往上走,2指向的是1,判断1是不是代表元素,1指向的是自己,1是代表元素.所以2元素所在的集合是1元素所在集合的集合.
以此类推,find(4)=3,find(3)=3.
find函数的扁平化处理
在并查集(Disjoint Set Union, DSU)中,find 函数的路径压缩(或称扁平化处理)是一种优化技术,旨在加速后续的查找操作。路径压缩通过在查找过程中将访问路径上的所有节点直接连接到根节点,减少树的高度,从而提高了查找和合并操作的效率。

当我们find(1)操作之后,得到的信息是1的代表元素是4,并且在这次寻找中走过的路径是1,2,3,那么将1,2,3全部直接指向代表元素4.
union(int a,int b)函数
cpp
void unionn(int x, int y) { // 合并操作
int fx = findd(x), fy = findd(y); // 查找 x 和 y 的根节点
father[fx] = father[fy]; // 将 x 的根节点指向 y 的根节点
}在并查集(Disjoint Set Union, DSU)中,union 函数用于将两个不同的集合合并为一个集合。union 函数通常结合 find 函数使用,以确保两个集合的代表(即根节点)被正确地连接在一起。

合并a,b元素,将两者归为同一集合,先查找a元素所在集合(代表元素)A,再查找b元素所在集合(代表元素)B,然后修改A指向B或者B指向A.
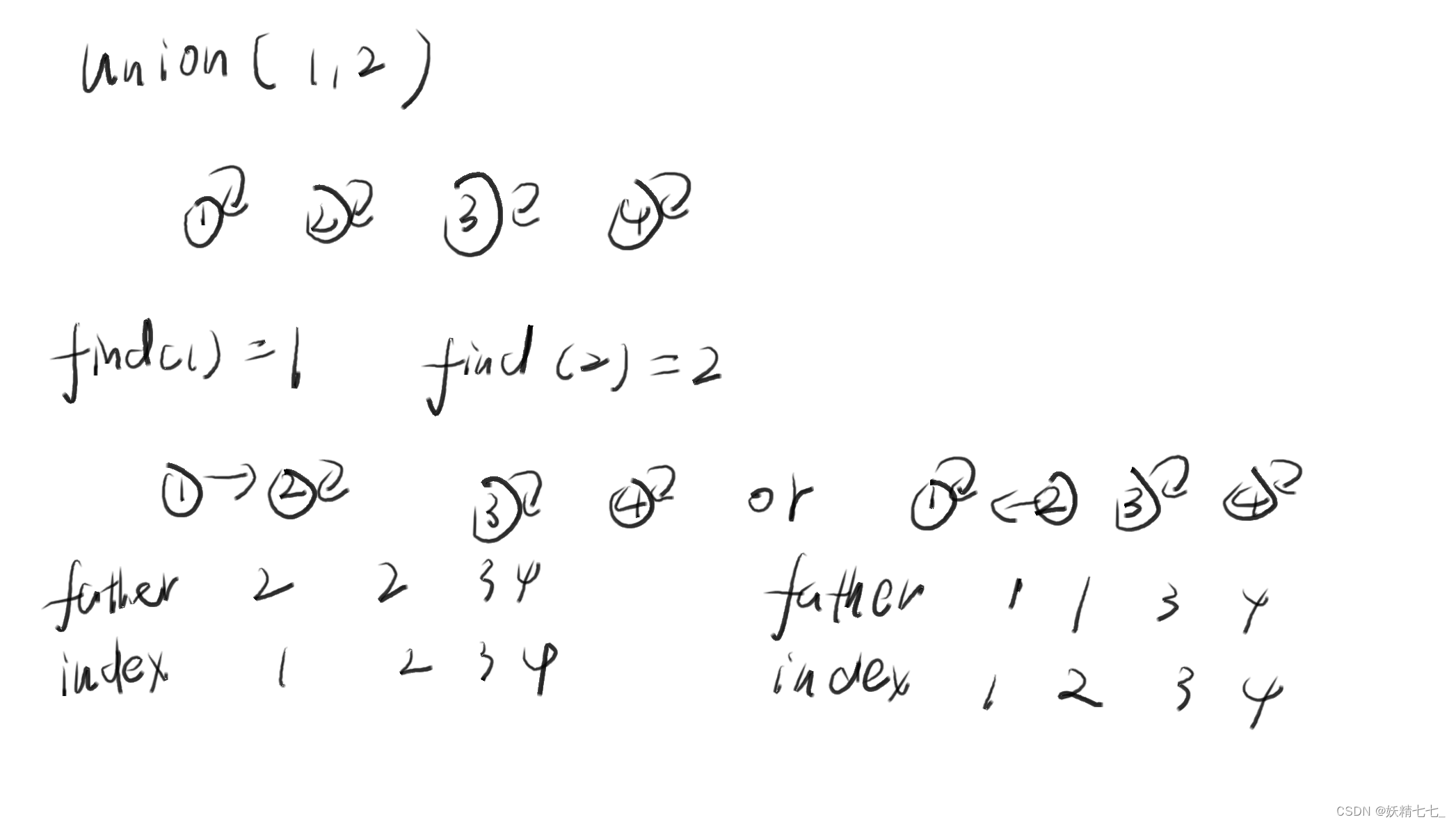
合并1,2元素.
1元素所在集合为1,2元素所在集合为2,1指向2或者2指向1.
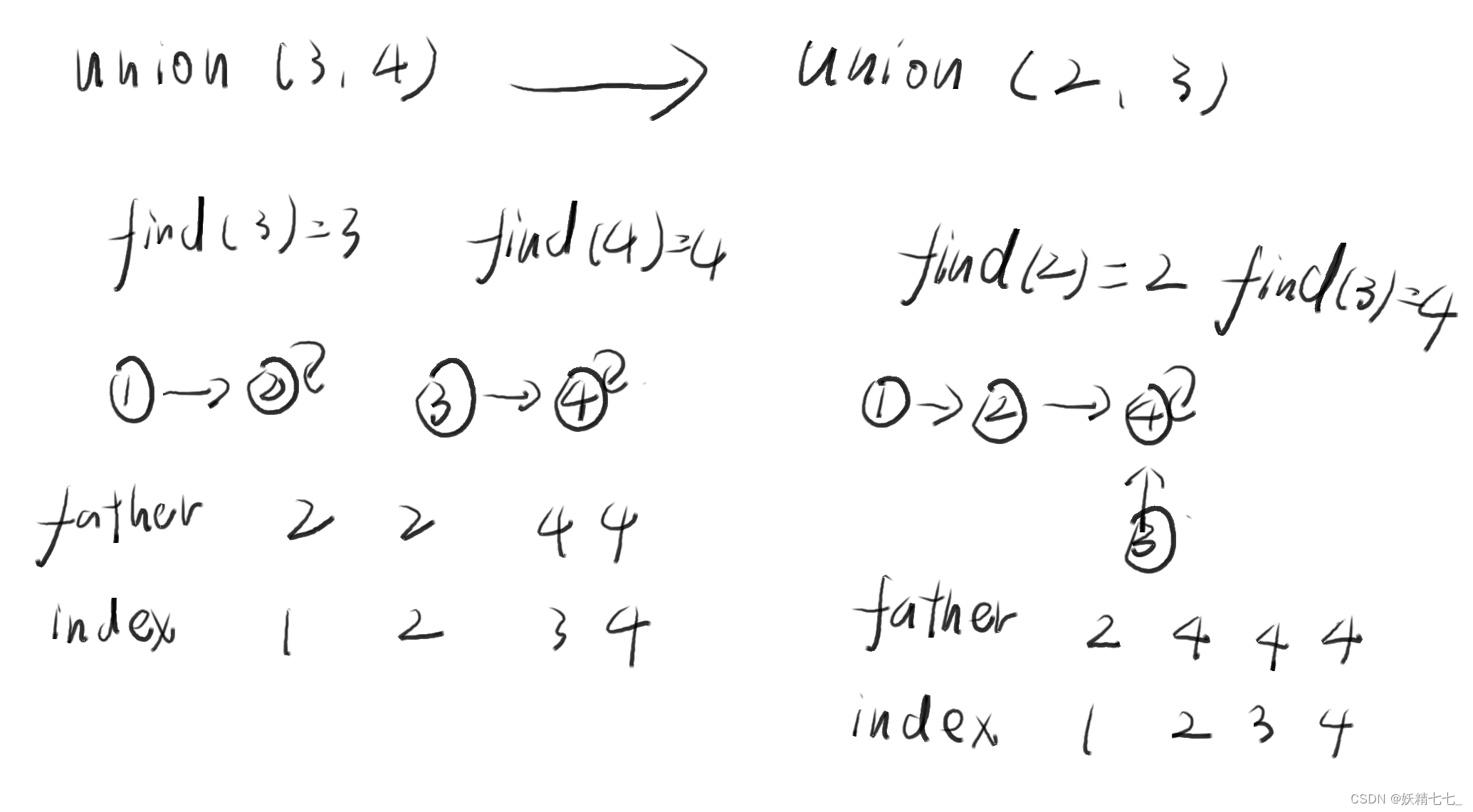
合并3,4元素.
查找3元素的代表元素,代表元素是3,查找4元素的代表元素,代表元素是4,3指向4.或者4指向3.
合并2,3元素.
查找2元素的代表元素,代表元素是2,查找3元素的代表元素,代表元素是4,2指向4.或者4指向2.
完整代码
cpp
#define debug // 定义调试宏
#ifdef debug // 如果定义了调试宏
#define o(x) #x<<"="<<(x)<<" " // 定义调试输出宏,输出变量名和值
#define bug(code) do{cout<<"L"<<__LINE__<<":";code;<<endl;}while(0) // 定义调试宏,在行号前输出调试信息
#else
#define bug(code) do{}while(0) // 如果未定义调试宏,则定义空宏
#endif
#include<bits/stdc++.h> // 引入所有标准库
using namespace std;
#define int long long // 定义 int 为 long long
#define endl '\n' // 定义 endl 为换行符
#define _(i,a,b) for(int i=a;i<=b;i++) // 定义正向循环宏
#define _9(i,a,b) for(int i=a;i>=b;i--) // 定义反向循环宏
int n, m; // 定义全局变量 n 和 m
struct node { // 定义结构体 node
int op, x, y; // 包含三个整数成员 op, x 和 y
};
vector<node> readd; // 定义存储 node 的向量 readd
vector<int> father; // 定义存储父节点的向量 father
vector<int> sizee; // 定义存储集合大小的向量 sizee
/*
find递归函数,含义是返回i元素所在集合的代表元素下标.
内部逻辑保证father[i]的维护.
如果father[i]=i是代表元素不需要维护直接返回father[i].
如果father[i]!=i说明不是代表元素,需要维护father[i]
走一步,当前节点的代表元素下标=findd(father[i]).
*/
int findd(int i) { // 查找操作,带路径压缩
if(father[i] != i) father[i] = findd(father[i]); // 如果 i 不是自己的父节点,递归查找父节点
return father[i]; // 返回父节点
}
/*
合并操作,维护sizee和father
father[fx]=father[fy]
代表元素是fy,fx再也用不到了.所以需要维护fy代表元素的信息,即sizee信息.
*/
void unionn(int x, int y) { // 合并操作
int fx = findd(x), fy = findd(y); // 查找 x 和 y 的根节点
if(fx != fy) sizee[fy] += sizee[fx]; // 如果根节点不同,合并集合,更新大小
father[fx] = father[fy]; // 将 x 的根节点指向 y 的根节点
}
void solve() {
father.assign(n + 5, 0); // 初始化 father 向量,大小为 n+5,值为 0
sizee.assign(n + 5, 1); // 初始化 sizee 向量,大小为 n+5,值为 1
_(i, 1, n) father[i] = i; // 初始化每个节点的父节点为自己
for(auto& xx : readd) { // 遍历所有操作
int op = xx.op, x = xx.x, y = xx.y, fx = findd(x), fy = findd(y); // 获取操作类型和操作数,并查找根节点
if(op == 1) { // 如果操作类型为 1
if(fx == fy) cout << "Yes" << endl; // 如果 x 和 y 在同一个集合,输出 "Yes"
else cout << "No" << endl; // 否则输出 "No"
} else { // 如果操作类型为 0
unionn(x, y); // 合并 x 和 y 所在的集合
}
}
}
signed main() {
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); // 快速输入输出
cin >> n >> m; // 输入 n 和 m
_(i, 1, m) { // 循环 m 次
node tt; // 定义临时变量 tt
cin >> tt.op >> tt.x >> tt.y; // 输入操作类型和操作数
readd.push_back(tt); // 将操作存入 readd 向量
}
solve(); // 调用 solve 函数处理操作
}结尾
最后,感谢您阅读我的文章,希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点,请随时在评论区留言。
同时,不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中,我将继续探讨这个话题的不同方面,为您呈现更多深度和见解。
谢谢您的支持,期待与您在下一篇文章中再次相遇!