APMCM亚太数学建模大赛的含金量在数学建模比赛中虽然不是最高水平,但是也属于比较高的水平了,值得参加试一试。
比如本次C题,
问题一:研究分析影响中国新能源汽车发展的主要因素,建立数学模型,描述这些因素对中国新能源汽车发展的影响。一般在建立模型前需要进行数据搜集与处理。
一般在数据分析或者建模前均需要进行数据预处理,比如对数据进行清洗,转换等等,数据预处理一般是减少数据分析和建模过程中的错误和偏差,所以进行数据预处理是十分有必要的,常见的数据预处理方式有异常值处理、缺失值处理、量纲化处理以及数据标签和数据编码。
异常值处理:
异常值也称离群值,也就是一组数据中,具有显著不同的特征或者数值的数据点,比如身高的数据中有一人身高为10m等等。常见的鉴别异常值标准由数字超过某个标准值,或者超过3倍标准差之外等。检验异常值的方法常见的有描述分析法、聚类、KNN以及图示法等,其中描述分析法和图示法比较简便,,如果数据中有异常值一般会设置null值(不参与分析)或者使用平均值、中位数、众数、随机数等进行填补。

缺失值处理
缺失值即在搜集数据或者进行实验等等,缺失的数据,对于缺失值处理常见的方法有将记录删除、直接分析(不进行处理)、线性插值以及该点线性趋势插值。
线性插值:在插值节点上的插值误差为0,只能用于一维数据。
线性趋势插值:在线性插值的基础上,对每个节点进行一次线性回归,得到该点的线性趋势,可以用于多维数据。
量纲化处理:
除了对异常值和缺失值处理外,一般数据还需要处理量纲问题,常见的量纲处理有标准化、归一化、中心化、正向化、逆向化、适度化、区间化等等。
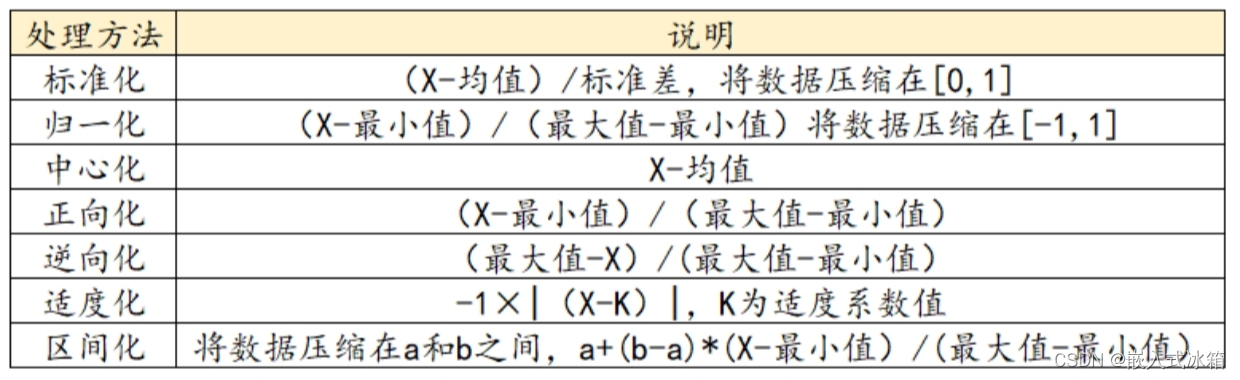
标准化:适用于数据分布不平衡情况,可以使得不同特征之间的数值范围不同的情况下,进行特征之间的比较,一般应用于聚类分析、主成分分析、探索性因子分析等较多。
归一化:适用于数据分布平衡的情况,使得不同特征之间的数值范围相同的情况下,进行特征之间的比较,但是如果数据中有异常值对归一化后的数据影响较大。
中心化:使不同特征之间的数据范围相同,中心化处理一般适用于数据分布不平衡且不需要进行特征之间的比较的情况。
正向化:一般多应用于评价模型中,正向的指标正向化,这种方法适用于指标值越大越好的情况,比如在分析中产品合格率等。
逆向化:一般多应用于评价模型中,逆向的指标逆向化,这种方法适用于指标值越小越好的情况,比如工厂的污染情况等。
适度化:这种方法适用于指标值差异较大的情况,比如消费者对某产品的满意度等。
区间化:这种方法适用于将数据固定压缩到某个范围内,区间化应该比较广,比如产品的质量控制等等。
数据编码及标签:
有的数据比如涉及赋值,1代表高中,2代表大专,3代表本科等等需要数据编码处理,其它如果数据组合形式或者反向题处理,也需要使用数据编码进行处理。数据标签一般用于标识数字的意义,比如某组数据中1代表不满足,2代表一般等等。
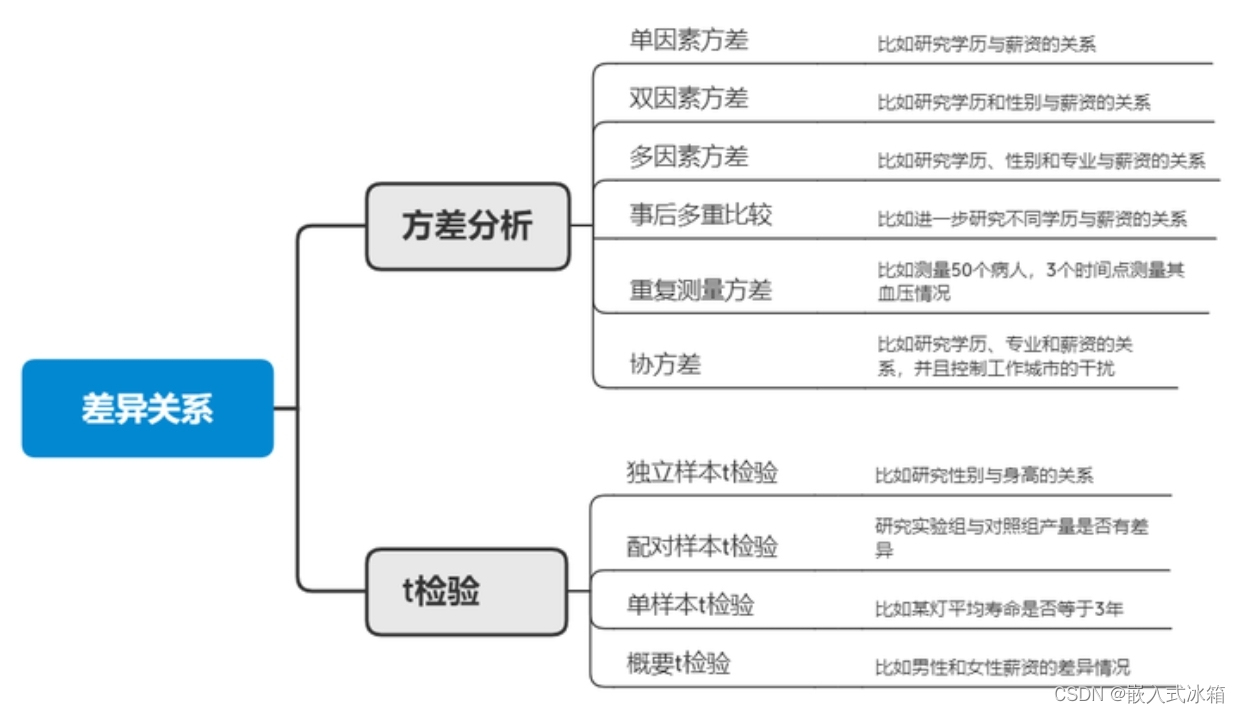
关系模型常见包括相关分析、差异分析、回归分析,在数学建模中关系模型可以解决很多问题。
相关分析
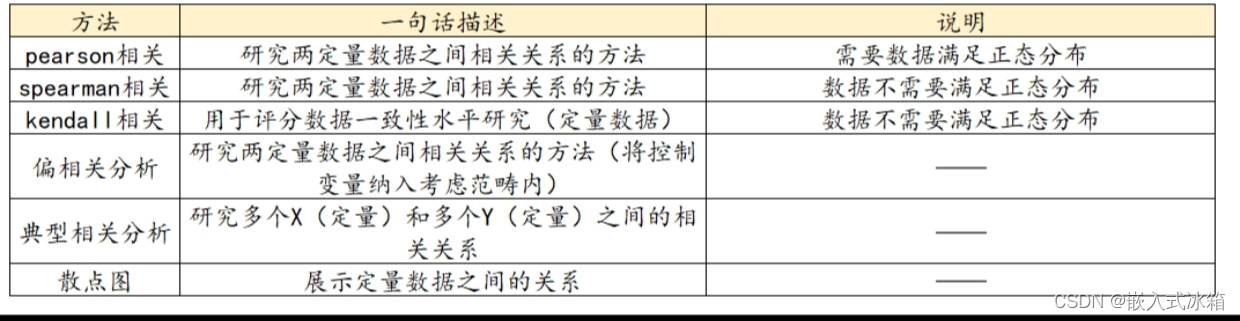
相关分析是解决数据之间相关性的一大类问题,不仅有常用的pearson相关,还有Spearman相关、kendall相关、偏相关分析。典型相关分析以及散点图等。
差异分析
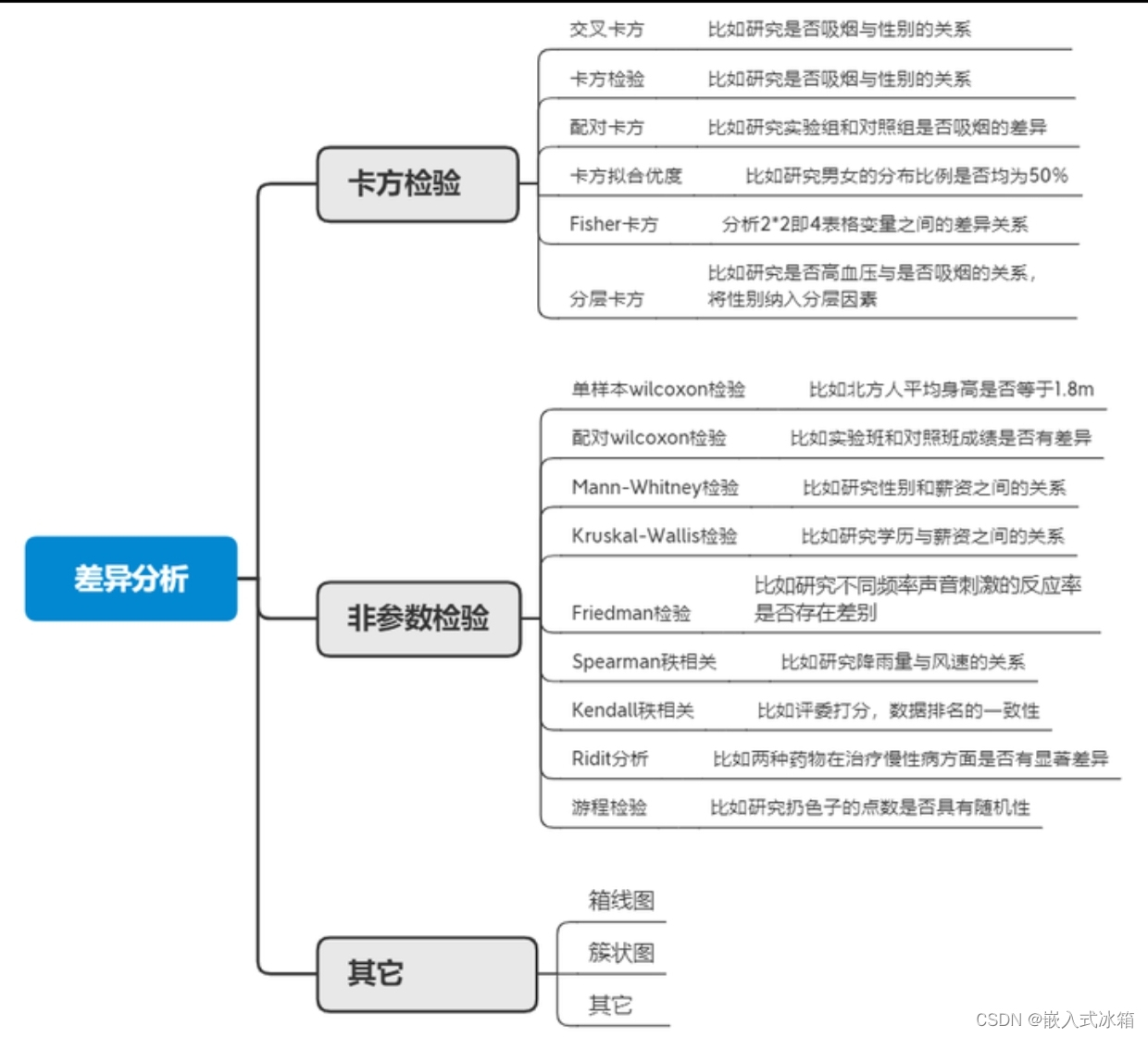
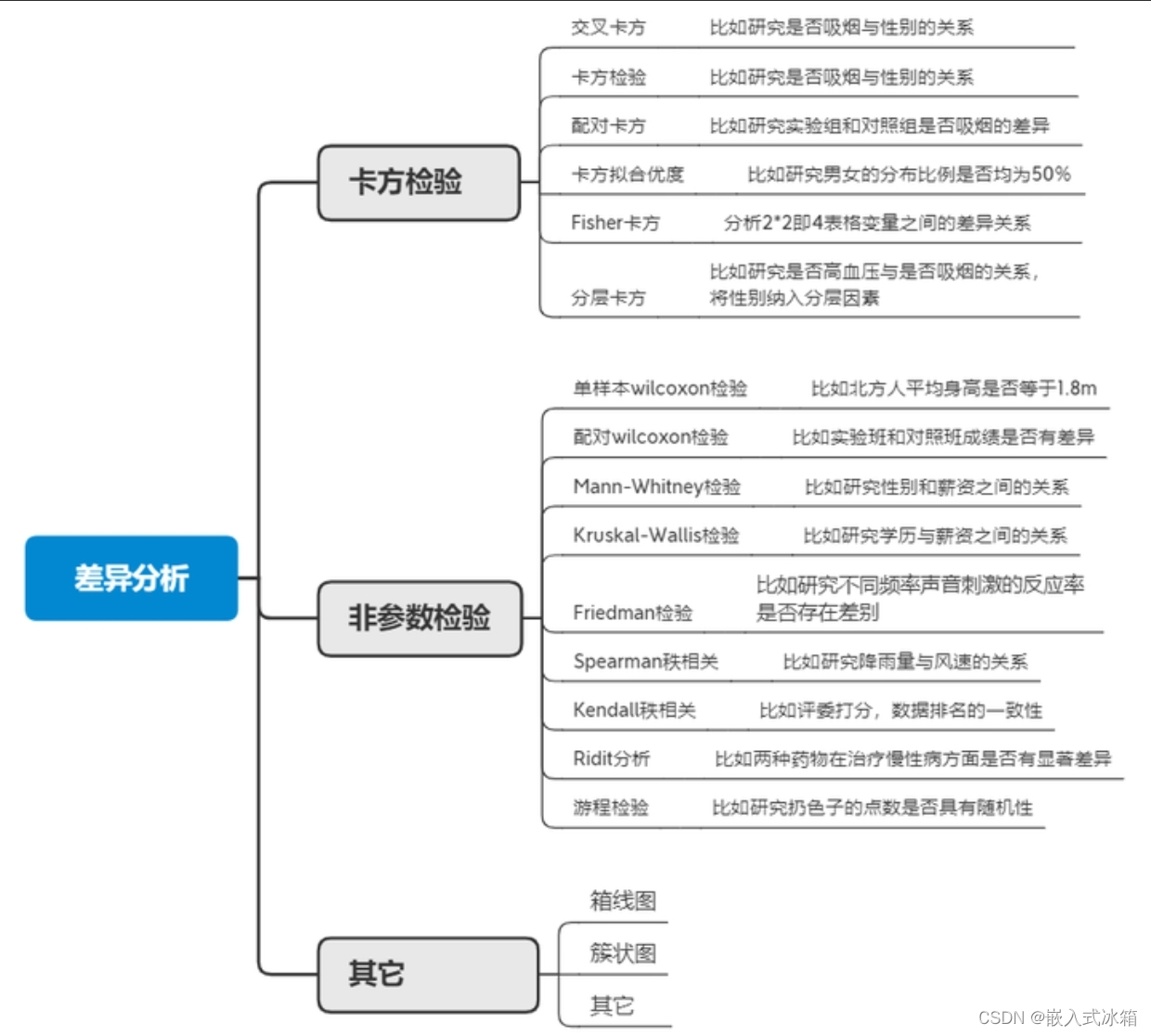
差异分析一般用于检测数据之间是否有差异以及差异是否显著,常见的差异分析有方差分析、t检验、卡方检验以及非参数检验,一般方差分析和t检验需要数据服从正态分布,如果不服从正态分布可以考虑使用非参数检验。
回归分析
回归分析一般研究变量间的影响关系,自变量对因变量的影响,常见的回归模型有线性回、logistic回归、生存分析等。如果因变量为定量数据则使用线性回归更合适,如果因变量为定类变量则使用logistic回归更合适。
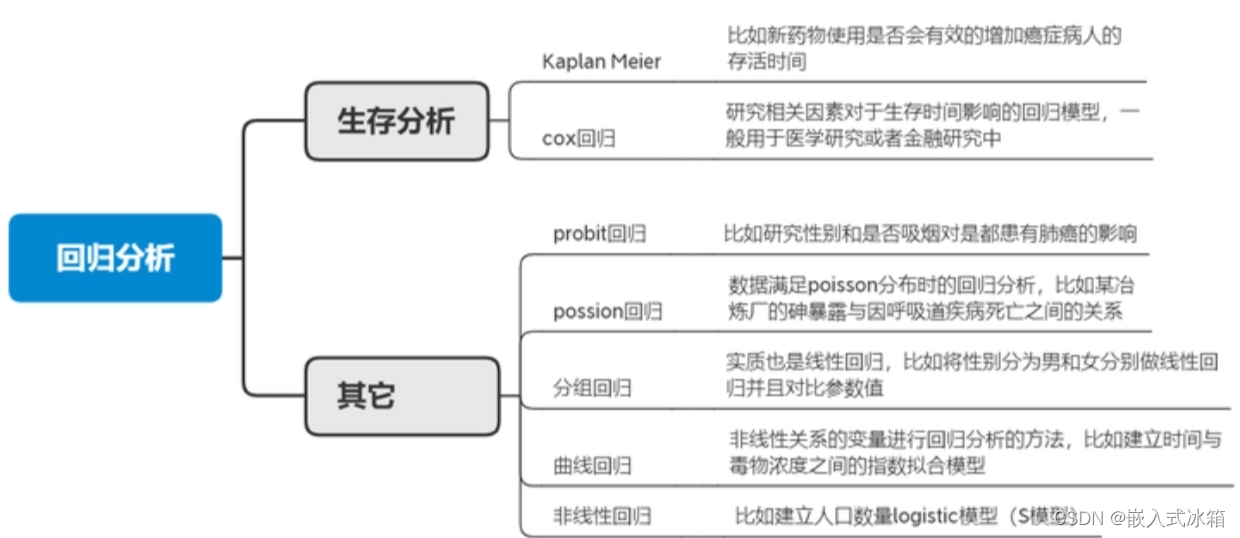
问题2 涉及预测模型
数学建模中的预测模型一般利用数据进行建立模型预测未来的趋势或者结果的方法,从而达到解决问题的目的,常见的方法有时间序列、回归分析、机器学习、马尔科夫预测或者其它方法组合预测等等。
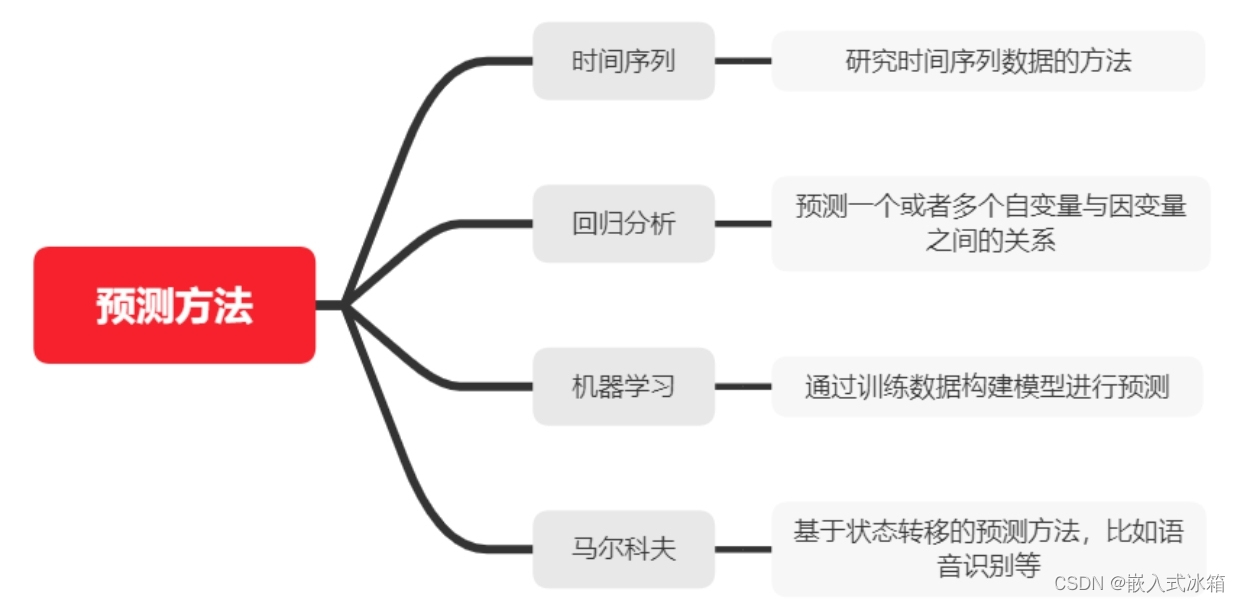
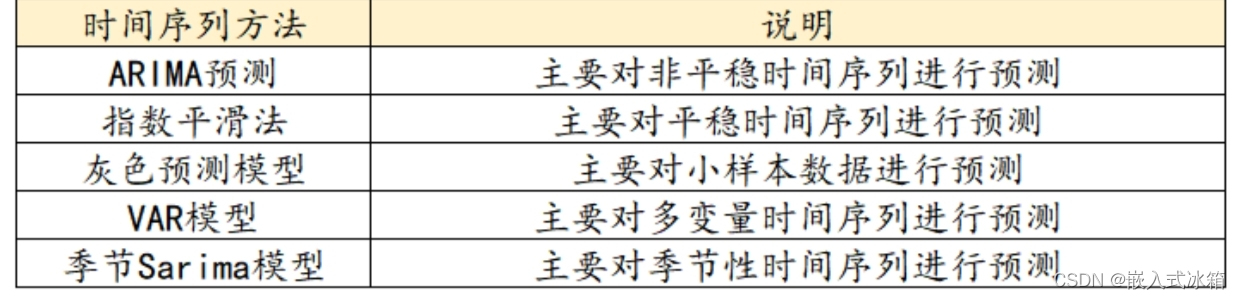
其中时间序列模型包括,ARIMA预测、指数平滑法、灰色预测模型、VAR模型以及季节Sarima模型。具体说明如下:
回归分析包括多元线性回归、logistic回归以及非线性回归等,机器学习包括决策树、随机森林、支持向量机、KNN、神经网络以及朴素贝叶斯等,具体可以参考以上描述的。
问题3分析对全球传统能源汽车行业的影响
可以使用回归模型或者权重评价分析等,具体的已经为大家整理好可以收藏此篇回答以备不时之需。
无论选择哪一个题型都需要使用数学模型进行解决模型,那么常见的数学模型有哪些呢?总结如下:
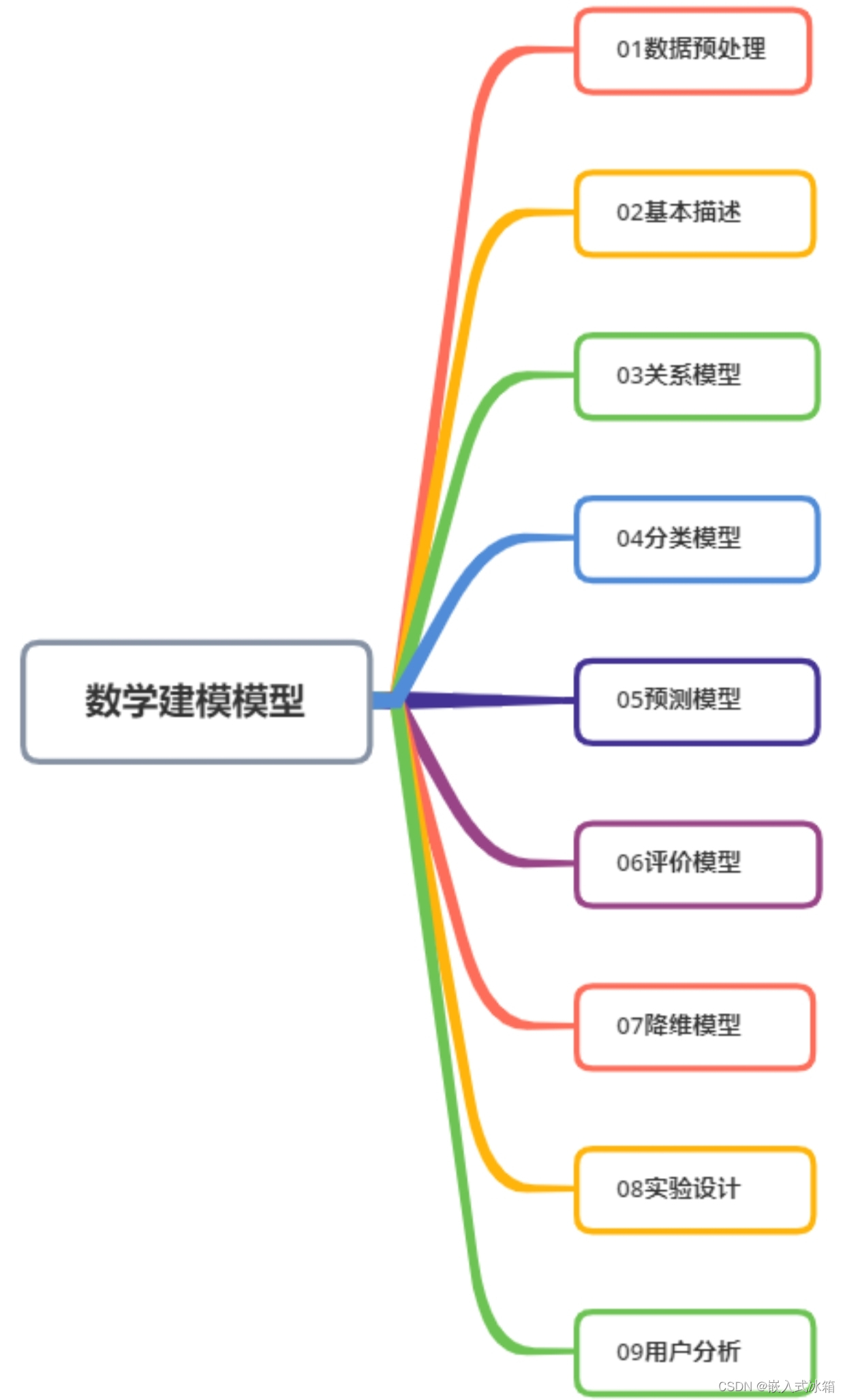
01数据预处理
一般在数据分析或者建模前均需要进行数据预处理,比如对数据进行清洗,转换等等,数据预处理一般是减少数据分析和建模过程中的错误和偏差,所以进行数据预处理是十分有必要的,常见的数据预处理方式有异常值处理、缺失值处理、量纲化处理以及数据标签和数据编码。
异常值处理:
异常值也称离群值,也就是一组数据中,具有显著不同的特征或者数值的数据点,比如身高的数据中有一人身高为10m等等。常见的鉴别异常值标准由数字超过某个标准值,或者超过3倍标准差之外等。检验异常值的方法常见的有描述分析法、聚类、KNN以及图示法等,其中描述分析法和图示法比较简便,,如果数据中有异常值一般会设置null值(不参与分析)或者使用平均值、中位数、众数、随机数等进行填补。

缺失值处理
缺失值即在搜集数据或者进行实验等等,缺失的数据,对于缺失值处理常见的方法有将记录删除、直接分析(不进行处理)、线性插值以及该点线性趋势插值。
线性插值:在插值节点上的插值误差为0,只能用于一维数据。
线性趋势插值:在线性插值的基础上,对每个节点进行一次线性回归,得到该点的线性趋势,可以用于多维数据。
量纲化处理:
除了对异常值和缺失值处理外,一般数据还需要处理量纲问题,常见的量纲处理有标准化、归一化、中心化、正向化、逆向化、适度化、区间化等等。
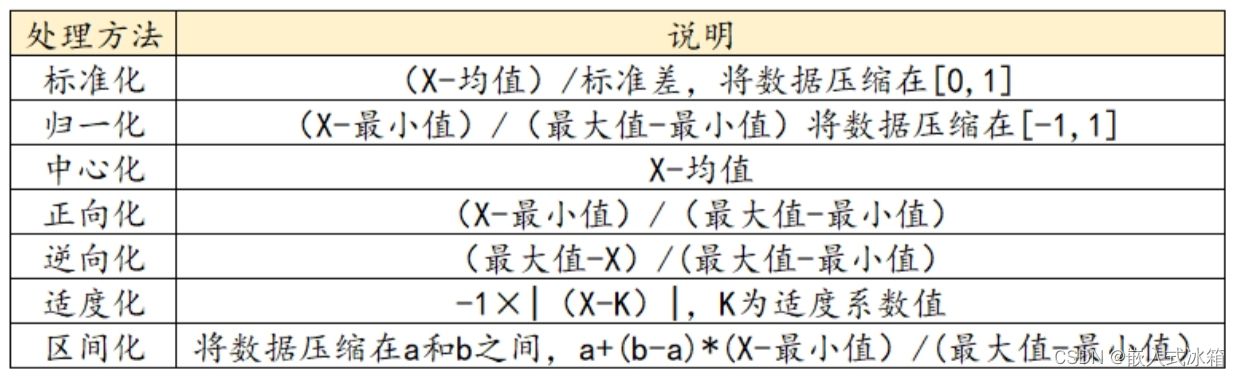
标准化:适用于数据分布不平衡情况,可以使得不同特征之间的数值范围不同的情况下,进行特征之间的比较,一般应用于聚类分析、主成分分析、探索性因子分析等较多。
归一化:适用于数据分布平衡的情况,使得不同特征之间的数值范围相同的情况下,进行特征之间的比较,但是如果数据中有异常值对归一化后的数据影响较大。
中心化:使不同特征之间的数据范围相同,中心化处理一般适用于数据分布不平衡且不需要进行特征之间的比较的情况。
正向化:一般多应用于评价模型中,正向的指标正向化,这种方法适用于指标值越大越好的情况,比如在分析中产品合格率等。
逆向化:一般多应用于评价模型中,逆向的指标逆向化,这种方法适用于指标值越小越好的情况,比如工厂的污染情况等。
适度化:这种方法适用于指标值差异较大的情况,比如消费者对某产品的满意度等。
区间化:这种方法适用于将数据固定压缩到某个范围内,区间化应该比较广,比如产品的质量控制等等。
数据编码及标签:
有的数据比如涉及赋值,1代表高中,2代表大专,3代表本科等等需要数据编码处理,其它如果数据组合形式或者反向题处理,也需要使用数据编码进行处理。数据标签一般用于标识数字的意义,比如某组数据中1代表不满足,2代表一般等等。
02基本描述
在正式分析前,还需要对数据的基本情况进行了解,比如数据最大值。最小值等等。常见查看数据基本特征的方法有统计分析法和图示法,统计分析法包括描述分析、频数分析以及分类汇总,图示法包括散点图、箱线图、直方图、簇状图、组合图以及帕累托图等。其中统计分析法是根据数据分析结果进行分析数据的特征,图示法主要是根据图形结合统计知识进行分析,图示法相对直观,统计分析法相对客观。
统计分析法:

03关系模型
关系模型常见包括相关分析、差异分析、回归分析,在数学建模中关系模型可以解决很多问题。
相关分析
相关分析是解决数据之间相关性的一大类问题,不仅有常用的pearson相关,还有Spearman相关、kendall相关、偏相关分析。典型相关分析以及散点图等。
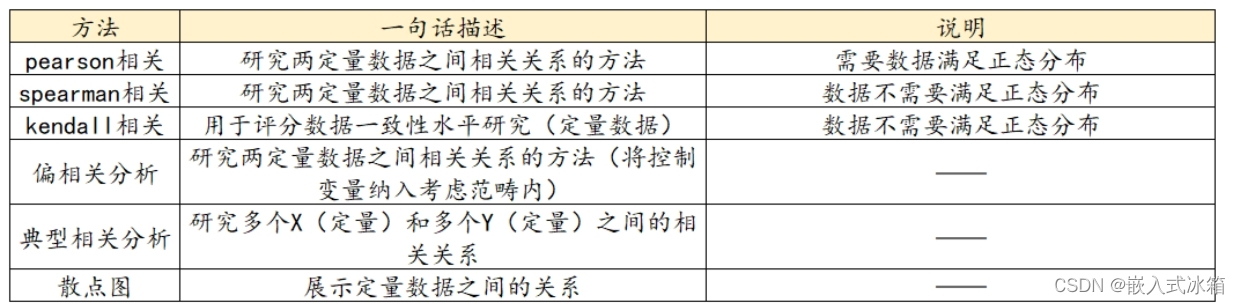
差异分析
差异分析一般用于检测数据之间是否有差异以及差异是否显著,常见的差异分析有方差分析、t检验、卡方检验以及非参数检验,一般方差分析和t检验需要数据服从正态分布,如果不服从正态分布可以考虑使用非参数检验。