1.概念
粒子群优化算法(Particle Swarm Optimization,PSO)是一种受鸟群、鱼群等群体智能行为启发的全局优化算法,由Kennedy和Eberhart于1995年提出。它通过模拟群体中个体之间的协作与竞争,实现对复杂优化问题的求解。
1. 核心思想
-
群体智能 :每个粒子代表一个潜在解,在搜索空间中飞行,通过跟踪个体历史最优(pbest )和群体历史最优(gbest)动态调整速度和位置。
-
迭代更新:粒子根据速度更新公式调整位置,逐步逼近最优解。
eg:有一群鸟要去找食物,
只要有一只鸟找到了食物就会给其他鸟发送信号,这个叫做群体最优 (gbest)
但是每一只鸟当然都记得自己曾经找到过的食物,还是有点留念,不舍得直接去其他地方找新的食物,这个叫做个体历史最优 (pbest)
鸟飞行还具有惯性,会保留一部分一开始飞行的方向(w)
这三者缺一不可,缺了就容易陷入局部最优
假如没有群体最优,鸟就容易过于迷恋以前找到的食物,而不会去探索其他食物更多的地方
假如没有个体最优,鸟就容易从众,有可能其他鸟找到的还没自己的好,直接放弃自己的食物会亏
惯性用于控制全局平衡,大值全局搜索,小值局部搜索
这样就可以使得鸟最后都飞到食物最多的地方(找到最优解)
2. 数学模型
确定下一步的位置主要由(w,pbest,gbest三个参数确定)
比如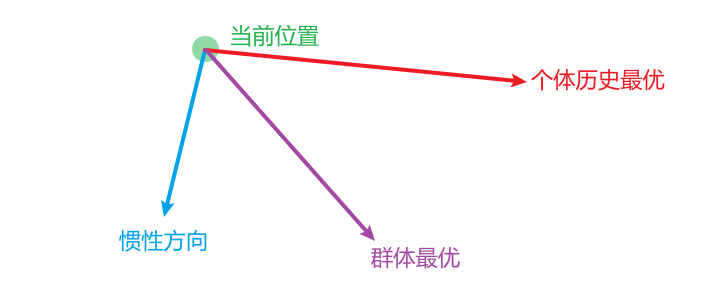
然后合成向量
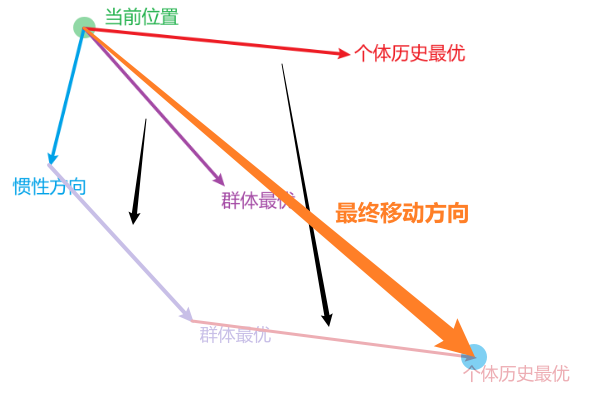
速度和位置更新公式
-
速度更新:
-
位置更新:
其中:
-
w:惯性权重(控制全局/局部搜索平衡)。
-
c1,c2:学习因子(认知和社会加速系数,通常取2)。
-
r1,r2:随机数([0,1]内均匀分布)。
-
3. 算法流程
-
初始化:随机生成粒子群的位置和速度。
-
评估适应度:计算每个粒子的目标函数值。
-
更新最优:
-
若当前粒子优于pbest ,则更新pbest。
-
若所有粒子中的最优优于gbest ,则更新gbest。
-
-
迭代更新:根据公式调整速度和位置,重复步骤2-3直至满足终止条件(如最大迭代次数或收敛精度)。
2.代码
1.初始化
Matlab
%% 1. 问题定义
objFun = @Rastrigin; % 目标函数句柄
D = 1; % 问题维度
lb = 0*ones(1,D); % 变量下界
ub = 50*ones(1,D); % 变量上界
%% 2. PSO 参数
SwarmSize = 40; % 粒子数
MaxIter = 200; % 最大迭代次数
w = 0.7298; % 惯性权重(SPSO 推荐常数)
c1 = 1.49618; % 认知系数
c2 = 1.49618; % 社会系数
vMax = 0.2*(ub-lb); % 最大速度(20% 搜索区间宽度)其中D(维度),lb,ub,objfun是自定义的,后面的权重就用推荐的就行
Matlab
%% 3. 初始化
rng default % 结果可复现
X = lb + (ub-lb).*rand(SwarmSize,D); % 位置
V = -vMax + 2*vMax.*rand(SwarmSize,D);% 速度
pBest = X; % 个体历史最优
pBestFit = arrayfun(@(i) objFun(X(i,:)), 1:SwarmSize);
[gBestFit,idx] = min(pBestFit);
gBest = pBest(idx,:);初始化,个体当前值记作个体历史最优
Matlab
pBestFit = arrayfun(@(i) objFun(X(i,:)), 1:SwarmSize);这一句比较麻烦,这里arrayfun一般是两个参数
其中第一个参数是函数部分,这里用的是匿名函数(lambda表达式)
匿名函数由两个部分组成,第一部分是参数:@(参数),空格隔开第二部分是函数:函数名(参数输入)因为不确定是多少维度,因此每一个参数可能由很多个维度,所以是X(i,:)
第二个部分是参数,就是把后面的参数一个一个带入函数,arrayfun再把函数的计算结果排成一个行向量,赋值给pbestfit
Matlab
[gBestFit,idx] = min(pBestFit);
gBest = pBest(idx,:);这里返回所有粒子里面的最小值,作为群体最优gbestfit,gbest是其位置
2.绘图函数
然后就是图像,这里我做了两个图像,
第一个图像是所有粒子的运动轨迹
第二个图像是最小值的变化过程,运行结果如图所示
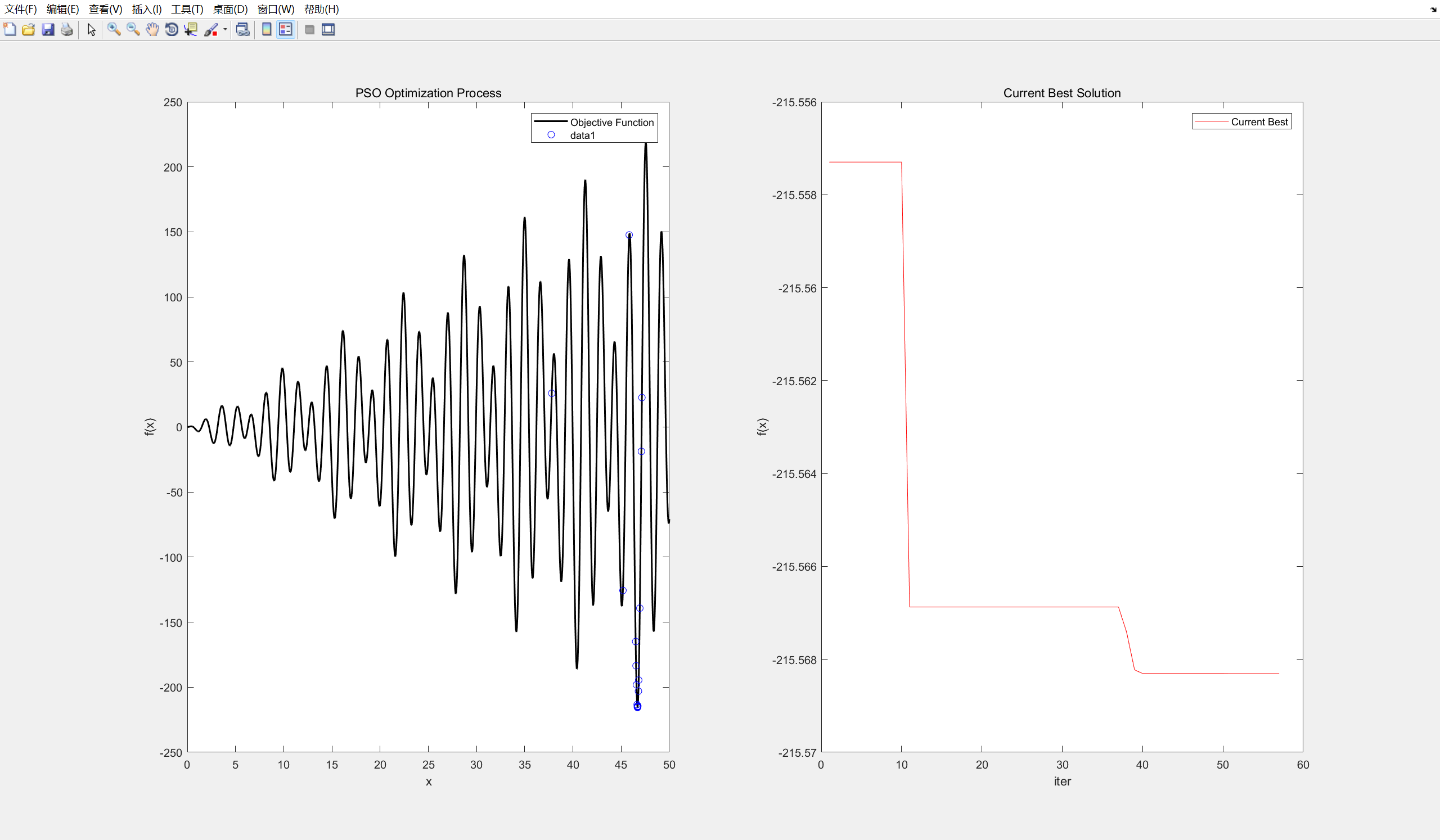
最后可以找到最小值
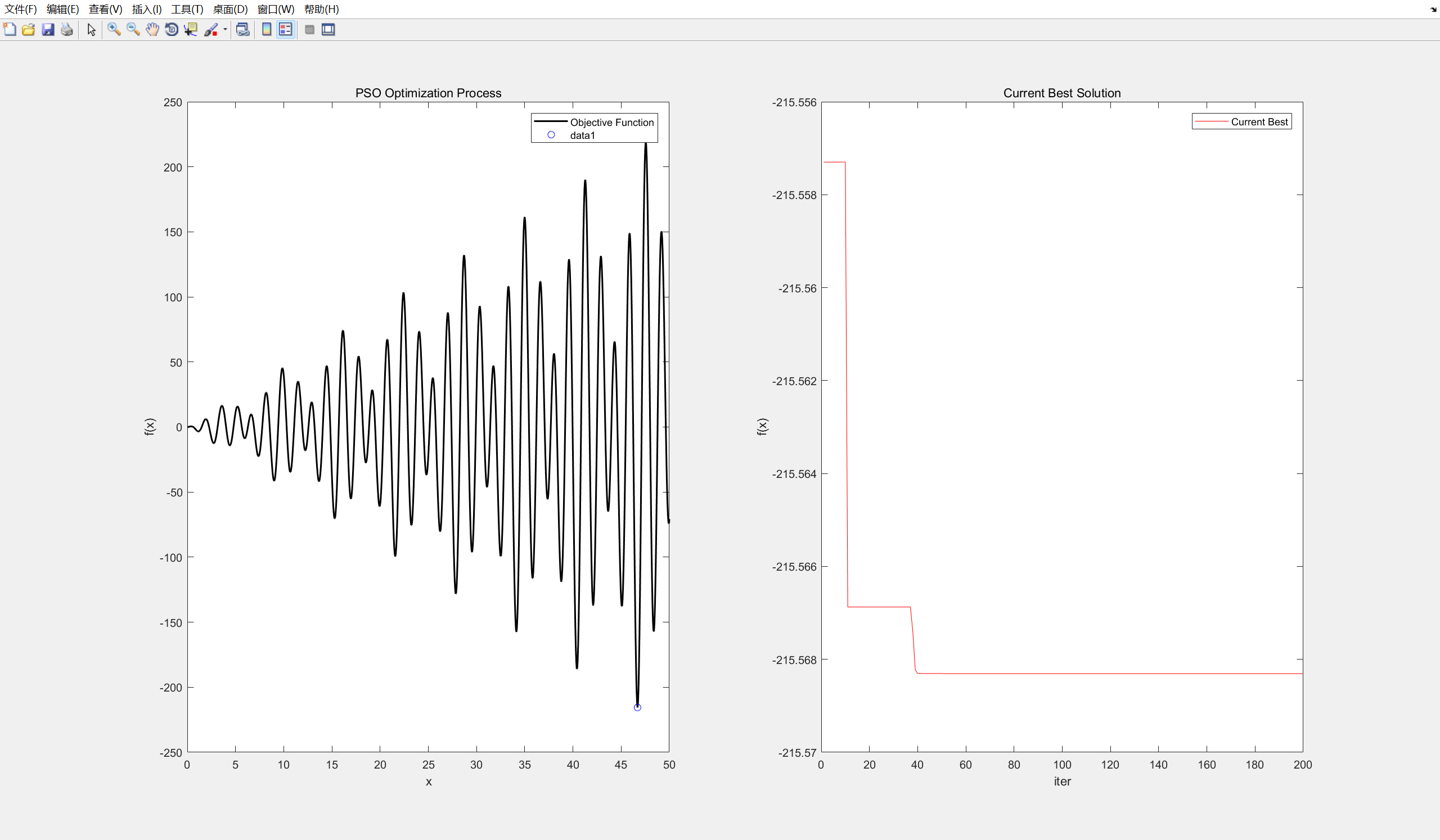
Matlab
% 绘制目标函数
x = linspace(0, 50, 1000);
y = arrayfun(objFun, x);
figure;
% 第一幅图:粒子的运动过程
subplot(1, 2, 1); % 1行2列的第1个位置
plot(x, y, 'k', 'LineWidth', 1.5);
hold on;
xlabel('x');
ylabel('f(x)');
title('PSO Optimization Process');
legend('Objective Function', 'Particles');
dot = plot(X, arrayfun(objFun, X), 'bo');
% 第二幅图:当前最优解
subplot(1, 2, 2); % 1行2列的第2个位置
plot(0, gBestFit, 'r-'); % 初始最优解
xlabel('iter');
ylabel('f(x)');
title('Current Best Solution');
legend('Current Best');legend是图例的意思
3.主函数

Matlab
%% 4. 迭代优化
trace = zeros(MaxIter,1); % 记录全局最优适应度
for iter = 1:MaxIter
trace(iter) = gBestFit;
for i = 1:SwarmSize
% 速度更新
V(i,:) = w*V(i,:) ...
+ c1*rand(1,D).*(pBest(i,:) - X(i,:)) ...
+ c2*rand(1,D).*(gBest - X(i,:));
% 速度边界处理(截断)
V(i,:) = max(V(i,:),-vMax); V(i,:) = min(V(i,:),vMax);
% 位置更新
X(i,:) = X(i,:) + V(i,:);
% 位置边界处理(反射/截断,这里用反射)
for d = 1:D
if X(i,d) < lb(d)
X(i,d) = lb(d);
V(i,d) = -V(i,d)*0.5;
elseif X(i,d) > ub(d)
X(i,d) = ub(d);
V(i,d) = -V(i,d)*0.5;
end
end
% 评估 & 更新个体最优
fit = objFun(X(i,:));
if fit < pBestFit(i)
pBest(i,:) = X(i,:);
pBestFit(i) = fit;
% 更新全局最优
if fit < gBestFit
gBest = X(i,:);
gBestFit = fit;
end
end
end
% 更新第一幅图:粒子的位置
set(dot, 'XData', X, 'YData', arrayfun(objFun, X));
% 更新第二幅图:当前最优解
subplot(1, 2, 2);
hold on;
% plot(iter, gBestFit, 'r.'); % 更新最优解
plot(1:iter, trace(1:iter), 'r-');
xlabel('iter');
ylabel('f(x)');
title('Current Best Solution');
legend('Current Best');
pause(0.1);
end4.输出结果
Matlab
%% 5. 结果
fprintf('\n最优解:\n'); disp(gBest);
fprintf('最优适应度:%.6g\n', gBestFit);
% figure;
% semilogy(trace,'LineWidth',1.5);
% xlabel('Iteration'); ylabel('Best f(x)');
% title('PSO Convergence Curve');
%% 6. 目标函数定义
function y = Rastrigin(x)
% A = 10;
y = x .* sin(x) .* cos(2*x) - 2*x .* sin(3*x) + 3*x .* sin(4*x);
end函数定义在最下面