程序猿成长之路之数据挖掘篇——决策树分类算法(1)——信息熵和信息增益

zygswo2024-06-22 19:24

决策树不仅在人工智能领域发挥着他的作用，而且在数据挖掘中也在分类领域中独占鳌头。了解决策树的思想是学习数据挖掘中的分类算法的关键，也是学习分类算法的基础。

什么是决策树

用术语来说，决策树（Decision Tree）是在已知各种情况发生概率的基础上，通过构成决策树来求取净现值的期望值大于等于零的概率，评价项目风险，判断其可行性的决策分析方法，是直观运用概率分析的一种图解法。由于这种决策分支画成图形很像一棵树的枝干，故称决策树。

用自己的话来说，决策树用于方便利用已知的数据和规律对未知的对象进行归类的方式，是一种分类算法。

使用决策树的意义

在应用于复杂的多阶段决策时，阶段明显，层次清楚，便于决策机构集体研究，可以周密地思考各种因素，有利于作出正确的决策。

分析决策树之前需要了解的内容

  1. 信息熵
    定义：
    从信息的完整性描述：当系统的有序状态一致时，数据越集中的地方熵值越小，数据越分散的地方熵值越大。
    从信息的有序性描述：当数据量一致时，系统越有序，熵值越低；系统越混乱或者分散，熵值越高。
    总而言之：
    信息熵的值越大，则认为该变量包含的信息量就大
    信息熵越大，表示包含的信息种类就越多，信息量就越大，信息越混乱分散，纯度就越低
    信息熵只和包含的信息种类、出现的概率有关，与信息总数量无关

信息熵计算公式

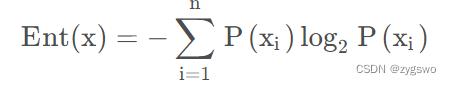
其中Ent(x) 为分类依据x的信息熵，P(xi)为第i类的数据在总数据中的数量占比。举个例子: 总数为15人的集合中，性别分为男和女，其中男生有8人，女生有7人，那么性别的信息熵为-(8/15)*log2(8/15)-(7/15)*log2(7/15)

  1. 信息增益
    定义：
    以某特征划分数据集前后的熵的差值。熵可以表示样本集合的不确定性，熵越大，样本的不确定性就越大。因此可以使用划分前后集合熵的差值来衡量使用当前特征对于样本集合D划分效果的好坏。也就是说如果信息增益越大，说明划分的效果越好，划分后数据集越有序，当前的分类依据越可靠。

信息增益的计算公式：

其中Gain(D,a) 表示根据某种规则分类中，a类数据在数据集D中的信息增益。

Ent(D)表示D的信息熵，Ent(D|a)表示条件熵，即根据某种规则分类中a类数据在数据集D中的信息熵

信息熵计算公式详见上文，条件熵计算公式如下:

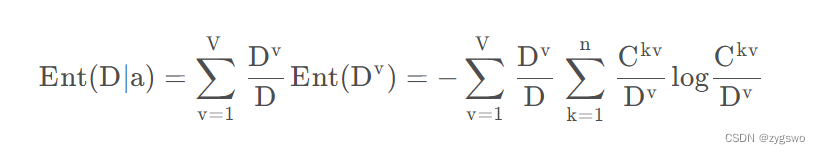
我们不难发现，条件熵相比信息熵前面还乘了一个系数，也就是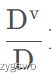

这个表示什么呢？就是按照这种规则分类中a类数据的个数除以数据样本总体个数得到的结果。

  1. 信息增益率
    定义：
    如果某个特征的特征值种类较多，则其信息熵值就越大。即：特征值种类越多，除以的系数就越大。如果某个特征的特征值种类较小，则其信息熵值就越小。即：特征值种类越小，除以的系数就越小。通过引入信息增益率，可以惩罚那些取值较多的特征，从而更倾向于选择那些取值较少但与目标变量相关性更强的特征。
    信息增益率 = 信息增益 / 信息熵
    信息增益率公式如下：

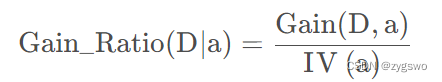
    其中IV(a)表示按照这种规则分类中属性a的信息熵，满足信息熵的计算公式。

如果大家看到这里有点蒙没关系，下面我会用一个例子简单的介绍一下信息熵、信息增益、信息增益率的计算。

案例

下图为一个列表，其中列举了不同性别和不同活跃度客户的流失情况，其中uid-用户编号，gender-性别，act_info-活跃度，is_lost-是否流失（0-否，1-是）

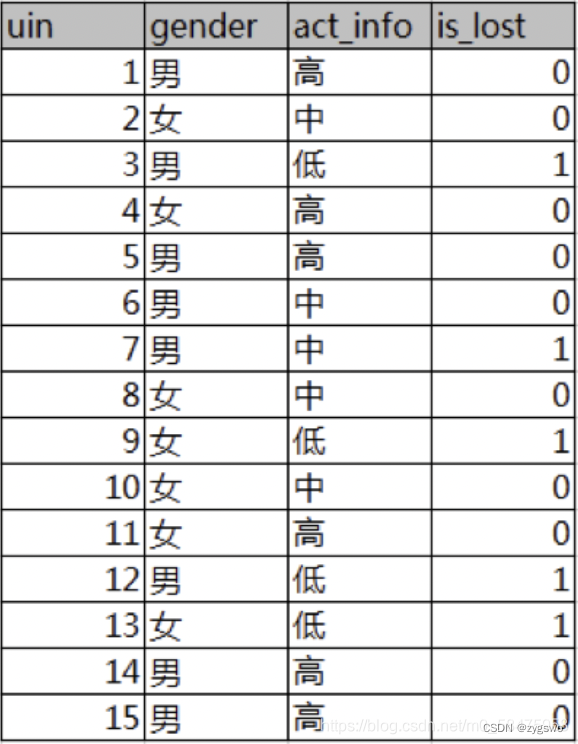
那么我们现在想分析一下性别和活跃度哪个条件更影响用户的流失情况。

思路

  1. 计算用户流失情况的信息熵
  2. 计算性别和活跃度条件下的信息增益。也就是计算不同条件下信息熵变化的情况
  3. 计算性别和活跃度条件下的信息增益率，从而对取值较多的特征进行过滤。
  4. 比较不同特征的信息增益率，取较高的那个作为首选特征

1. 计算用户流失情况的信息熵

首先我们由图可知，流失的用户有5人，编号分别是3、7、9、12、13，非流失客户有10人，那么我们有：

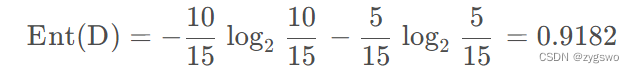
也就是流失情况的信息熵为0.9182,由于信息熵高，因此数据混乱度较高。

2. 计算性别和活跃度条件下的信息增益。

性别条件下的信息增益：

由图中我们有男生中未流失的用户有5人，流失的客户有3人，分别是编号3，7，12


同理可以计算女生的信息熵，因此有

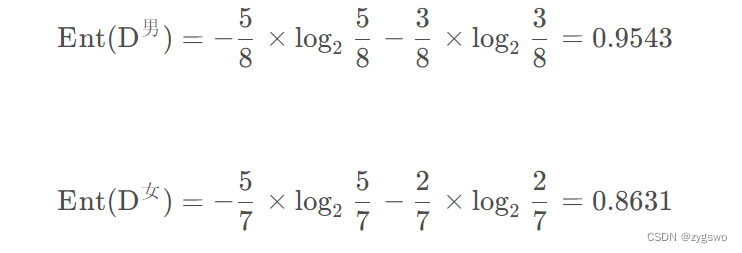
计算性别条件下的信息增益：

其中Ent(D|a)为条件熵，在信息熵的基础上乘了一个频率比例。（a样本个数/D-总样本数）

最终得到信息增益为0.0064，可以看出这个条件的信息增益很小，也说明这个条件对于用户是否会流失的影响很小。

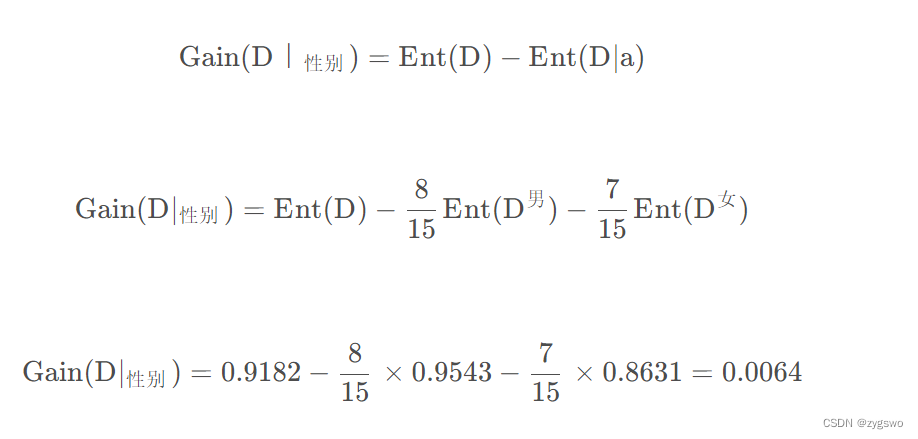
活跃度条件下的信息增益：

计算信息熵:

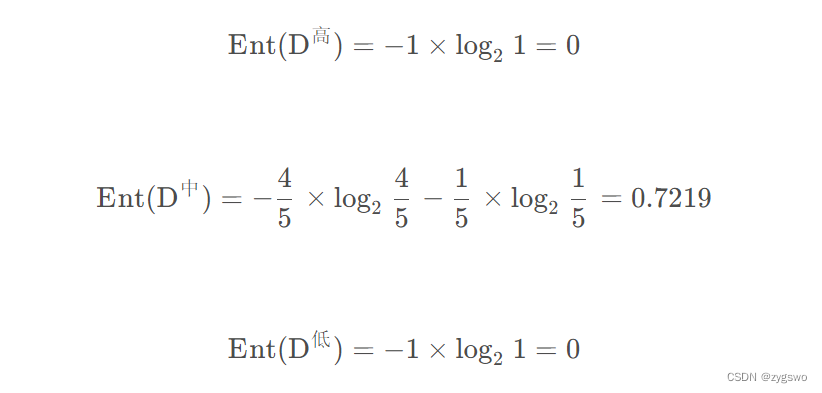
之后计算活跃度的信息增益：

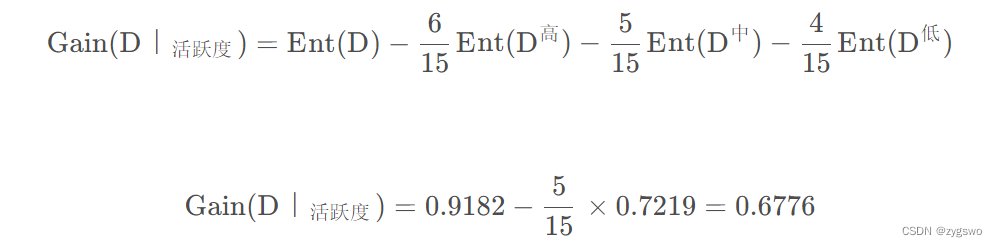
从这里我们可以看出活跃度对于用户流失的影响要远大于用户的性别。

3. 计算性别和活跃度条件下的信息增益率

性别的信息熵：

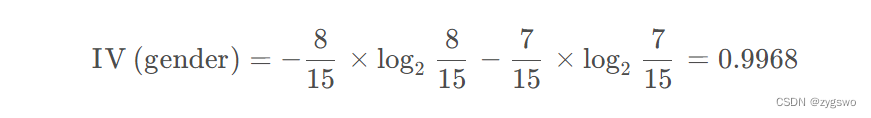
活跃度的信息熵：

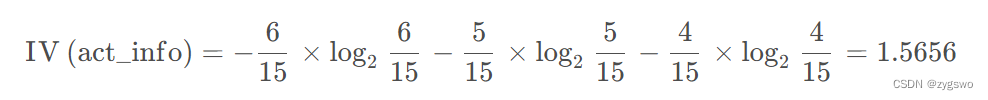
上文已经计算好了信息增益：

性别的信息增益为：0.0064

活跃度的信息增益为：0.6776

所以我们有：

性别的信息增益率为：

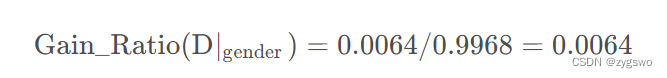
活跃度的信息增益率为：

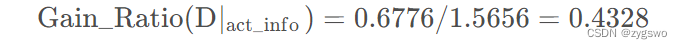
根据以上计算结果：性别特征的信息增益率明显小于活跃度的信息增益率，因此我们优先选用活跃度作为分类特征

案例实现代码

java 复制代码 
package classificationUtil;

import java.io.BufferedInputStream;
import java.io.File;
import java.io.FileInputStream;
import java.io.IOException;
import java.lang.reflect.Field;
import java.util.ArrayList;
import java.util.List;
import java.util.Map;
import java.util.concurrent.ConcurrentHashMap;

import com.alibaba.fastjson.JSON;  //需要自行导入

/**
 * decisionTreeUtil
 * @author zygswo
 *
 */
public class decisionTreeUtil {
	
	public static void main(String[] args) {
		run();
	}
	
	public static void run() {
		File dataFile = new File("D:/decisionTree/dataset/datas.txt"); //读取文件
		BufferedInputStream reader = null;
		String itemsStr = "";
		double totalNb = 0; //总数
		List<TestItemNorm> items = new ArrayList<>();
		try {
			if (!dataFile.exists()) {
				dataFile.createNewFile();
			}
			reader = new BufferedInputStream(new FileInputStream(dataFile));
			byte[] line = new byte[reader.available()];
			reader.read(line);
			itemsStr = new String(line);
			System.out.println(itemsStr);
			items = JSON.parseArray(itemsStr,TestItemNorm.class);
			//将总数保存到totalNb中，方便计算信息增益
			totalNb = items.size(); 
			//计算is_lost数量
			Map<String,List<TestItemNorm>> isLostRes = calcNb(items,"is_lost");
			//计算is_lost信息熵
			double isLostXinxiShangRes = calcXinxishang(isLostRes);
			System.out.println("is_lost类别的信息熵为  = " + isLostXinxiShangRes);
			
			
			//计算信息增益
			//计算性别的信息增益
			//计算不同性别的数量
			Map<String,List<TestItemNorm>> genderRes = calcNb(items,"gender");
			//计算信息增益
			double genderXinxiZengyiRes = isLostXinxiShangRes;
			//根据不同的性别去求值
			for (Map.Entry<String, List<TestItemNorm>> entry:genderRes.entrySet()) {
				List<TestItemNorm> resTmp = entry.getValue();
				//求当前
				Map<String,List<TestItemNorm>> temp = calcNb(resTmp,"is_lost");
				double xinxiShangTemp = calcXinxishang(temp);
				genderXinxiZengyiRes = genderXinxiZengyiRes - (resTmp.size() * xinxiShangTemp / totalNb * 1.0);
			}
			System.out.println("性别的信息增益为  = " + genderXinxiZengyiRes);
			
			//计算活跃度的信息增益
			//计算不同活跃度的数量
			Map<String,List<TestItemNorm>> activeRes = calcNb(items,"act_info");
			//计算信息增益
			double huoyueduXinxiZengyiRes = isLostXinxiShangRes;
			//根据不同的性别去求值
			for (Map.Entry<String, List<TestItemNorm>> entry:activeRes.entrySet()) {
				List<TestItemNorm> resTmp = entry.getValue();
				//求当前
				Map<String,List<TestItemNorm>> temp = calcNb(resTmp,"is_lost");
				double xinxiShangTemp = calcXinxishang(temp);
				huoyueduXinxiZengyiRes = huoyueduXinxiZengyiRes - (resTmp.size() * xinxiShangTemp / totalNb * 1.0);
			}
			System.out.println("活跃度的信息增益为 = " + huoyueduXinxiZengyiRes);
			
			//计算信息增益率
			//计算信息熵
			double genderRate = calcXinxishang(genderRes);
			System.out.println("性别的信息熵为 = " + genderRate);
			double huoyueduRate = calcXinxishang(activeRes);
			System.out.println("活跃度的信息熵为 = " + huoyueduRate);
			//计算信息增益率
			genderRate = genderXinxiZengyiRes / (genderRate * 1.0);
			System.out.println("性别的信息增益率为 = " + genderRate);
			huoyueduRate = huoyueduXinxiZengyiRes / (huoyueduRate * 1.0);
			System.out.println("活跃度的信息增益率为 = " + huoyueduRate);
			
			//构建决策树
		} catch (IOException e) {
			// TODO Auto-generated catch block
			e.printStackTrace();
		} finally {
			try {
				reader.close();
			} catch (IOException e) {
				// TODO Auto-generated catch block
				e.printStackTrace();
			}
		}
	}
	
	/**
	 * 计算信息熵
	 * @param inputDataSet 输入的结果集
	 * @return 信息熵
	 */
	private static <T> double calcXinxishang(Map<String, List<T>> inputDataMap) {
		double totalNb = 0.0,res = 0.0;
		//计算总数
		for (Map.Entry<String, List<T>> entry:inputDataMap.entrySet()) {
			if (entry.getValue() == null) {
				continue;
			}
			totalNb += entry.getValue().size();
		}
		//计算信息熵
		for (Map.Entry<String, List<T>> entry:inputDataMap.entrySet()) {
			if (entry.getValue() == null) {
				continue;
			}
			int currentSize = entry.getValue().size();
			double temp = (currentSize / totalNb) * 1.0;
			if (res == 0) {
				res = -1 * temp * (Math.log(temp) / Math.log(2) * 1.0);
			} else {
				res += -1 * temp * (Math.log(temp) / Math.log(2) * 1.0);
			}
		}
		return res;
	}

	/**
	 * 计算数量统计结果
	 * @param inputDataSet 输入的结果集
	 * @param calcColumnName 列名
	 * @return 统计结果
	 */
	private static <T> Map<String,List<T>> calcNb(List<T> inputDataSet,String calcColumnName){
		Map<String,List<T>> res = new ConcurrentHashMap<String, List<T>>();
		if (inputDataSet == null || inputDataSet.isEmpty()) {
			return res;
		}
		Class<?> cls = inputDataSet.get(0).getClass();
		Field[] fs = cls.getDeclaredFields();
		//
		for (Field f:fs) {
			f.setAccessible(true);
			String name = f.getName();
			if (name.equalsIgnoreCase(calcColumnName)) {
				for (T inputData:inputDataSet) {
					try {
						String value = f.get(inputData).toString();
						List<T> temp = new ArrayList<>();
						if (res.get(value) != null) {
							temp = res.get(value);
						}
						temp.add(inputData);
						res.put(value, temp);
					} catch (IllegalArgumentException e) {
						// TODO Auto-generated catch block
						e.printStackTrace();
					} catch (IllegalAccessException e) {
						// TODO Auto-generated catch block
						e.printStackTrace();
					}
				}
			}
		}
		return res;
	}
}

参考：
机器学习：决策树之信息熵、信息增益、信息增益率、基尼指数分析https://blog.csdn.net/m0_58475958/article/details/118735363

相关推荐
IT古董5 小时前
【机器学习】机器学习的基本分类-强化学习-策略梯度（Policy Gradient，PG）
人工智能·机器学习·分类
落魄君子5 小时前
GA-BP分类-遗传算法（Genetic Algorithm）和反向传播算法（Backpropagation）
算法·分类·数据挖掘
四口鲸鱼爱吃盐5 小时前
Pytorch | 从零构建GoogleNet对CIFAR10进行分类
人工智能·pytorch·分类
落魄君子5 小时前
ELM分类-单隐藏层前馈神经网络（Single Hidden Layer Feedforward Neural Network, SLFN）
神经网络·分类·数据挖掘
爱喝热水的呀哈喽6 小时前
《机器学习》支持向量机
人工智能·决策树·机器学习
四口鲸鱼爱吃盐6 小时前
Pytorch | 从零构建MobileNet对CIFAR10进行分类
人工智能·pytorch·分类
call me by ur name10 小时前
VLM--CLIP作分类任务的损失函数
人工智能·机器学习·分类
Python机器学习AI10 小时前
分类模型的预测概率解读：3D概率分布可视化的直观呈现
算法·机器学习·分类
机器学习之心14 小时前
BiTCN-BiGRU基于双向时间卷积网络结合双向门控循环单元的数据多特征分类预测（多输入单输出）
深度学习·分类·gru
qingyunliushuiyu15 小时前
企业为何需要可视化数据分析系统
数据挖掘·数据分析·数据采集·数据可视化·数据分析系统
热门推荐
01〔AI 绘画〕Stable Diffusion 之 解决绘制多人或面部很小的人物时面部崩坏问题 篇02ARM学习（31）编译器对overlay方式的支持03玄机平台应急响应—webshell查杀04DisplayPort AltMode On Type-c协议_Ver2.0(学习笔记)05校验 GPT-4 真实性的三个经典问题：快速区分 GPT-3.5 与 GPT-4，并提供免费测试网站06Docker 夺命连环 15 问076个主流的工业3D管道设计软件08基于大语言模型（LLM）的合成数据生成、策展和评估的综述09(欧拉)openEuler系统添加网卡文件配置流程、(欧拉)openEuler系统手动配置ipv6地址流程、(欧拉)openEuler系统网络管理说明10树莓派 5 AI 套件（Hailo-8L）使用教程