1 原理
在图像增强中,线性变换、非线性变换(包括伽马变换和对数变换)以及直方图均衡化是常用的技术。以下是这些技术的原理和标准公式:
1.1 线性变换
线性变换主要用于调整图像的对比度和亮度。它通过改变像素值的线性映射关系来实现,公式如下:
S = k × r + b
- S:输出变量(变换后的像素值)
- r:输入变量(原始像素值)
- k:倍数因子(控制对比度)
- b:偏移因子(控制亮度)
1.2 非线性变换
本文采用伽马变换与对数变换。
1.2.1 伽马变换(Gamma Transformation)
伽马变换是一种常用的非线性灰度变换方法,用于调整图像的对比度。它基于光照强度与人眼感知之间的非线性关系。
g(x, y) = c × [f(x, y)]^γ
- g(x, y):变换后的像素值
- f(x, y):原始像素值
- c:常数,用于控制对比度的增益
- γ:伽马值,用于调整亮度的曲线形状。当γ > 1时,增加了高灰度级之间的对比度;当γ < 1时,增加了低灰度级之间的对比度。
1.2.2 对数变换
对数变换通过拉伸低灰度级并压缩高灰度级来增强图像的暗部细节。
g(x, y) = c × log(1 + f(x, y))
- g(x, y):变换后的像素值
- f(x, y):原始像素值
- c:常数,用于控制对比度的增益
1.3 直方图均衡化
直方图均衡化通过调整图像的灰度级分布,使得图像中的像素更加均匀地分布在整个灰度级范围内,从而增强图像的整体对比度。
- s_k:输出灰度级
- n:图像中像素的总和
- n_j:当前灰度级的像素个数
- k:灰度级索引(0到L-1,L是图像中可能的灰度级总数)
综上所述:
- 线性变换通过调整倍数因子和偏移因子来改变图像的对比度和亮度。
- 非线性变换(如伽马变换和对数变换)基于非线性函数来调整图像的灰度级,以实现特定的对比度增强效果。
- 直方图均衡化通过调整图像的灰度级分布来增强图像的整体对比度。
2 代码
Matlab
%% 线性变换进行图像增强
I2= imread('test.jpeg');
J2=rgb2gray(I2);
figure;
subplot(2,2,1), imshow(J2) ;
title('原始图像');
subplot(2,2,2), imhist(J2) ;%显示原始图像的直方图
title('原始灰度直方图');
K = imadjust(J2,[0.4 0.6],[]);%使用imadjust函数进行灰度的线性变换
subplot(2,2,3), imshow(K);
title('线性变换后的灰度图像');
subplot(2,2,4),imhist(K)%显示变换后图像的直方图
title('线性变换后的灰度直方图');
%% 伽马变换进行图像增强
figure;
subplot(3,2,1), imshow(J2) ;
title('原始图像');
subplot(3,2,2), imhist(J2) ;%显示原始图像的直方图
title('原始灰度直方图');
gamma = 0.5;
I_gamma = imadjust(J2, [], [], gamma);
subplot(3,2,3),imshow(I_gamma);
title('伽马变换后的灰度图像');
subplot(3,2,4),imhist(I_gamma);
title('伽马变换后的灰度直方图');
%% % 对数变换进行图像增强
c = 0.5; % 控制参数,用于避免log(0)
I_log = c * log(1 + double(J2)) / log(256);
I_log = im2uint8(I_log);
subplot(3,2,5);
imshow(I_log);
title('对数变换后的图像');
subplot(3,2,6);
imhist(I_log);
title('对数变换后的灰度直方图');
%%
figure('Position',[50 50 800 600])
subplot(4,2,1), imshow(J2);
title('原始图像');
subplot(4,2,2), imhist(J2);
title('原始灰度直方图');
subplot(4,2,3), imshow(K);
title('线性变换后的灰度图像');
subplot(4,2,4),imhist(K)%显示变换后图像的直方图
title('线性变换后的灰度直方图');
subplot(4,2,5),imshow(I_gamma);
title('伽马变换后的灰度图像');
subplot(4,2,6),imhist(I_gamma);
title('伽马变换后的灰度直方图');
subplot(4,2,7),imshow(I_log);
title('对数变换后的图像');
subplot(4,2,8),imhist(I_log);
title('对数变换后的灰度直方图');
%% 直方图均衡化进行图像增强
I3 = imread('test.jpeg'); % 读取图像
I_gray = rgb2gray(I3); % 转换为灰度图像
% 直方图均衡化
I_eq = histeq(I_gray);
% 显示原始图像和增强后的图像
figure;
subplot(2, 2, 1),imshow(I_gray);
title('原始图像');
subplot(2, 2, 2);
imhist(I_gray),title('原始灰度直方图');
subplot(2, 2, 3),imshow(I_eq);
title('直方图均衡化后的图像');
subplot(2, 2, 4),imhist(I_eq);
title('直方图均衡化后的灰度直方图');3 运行结果
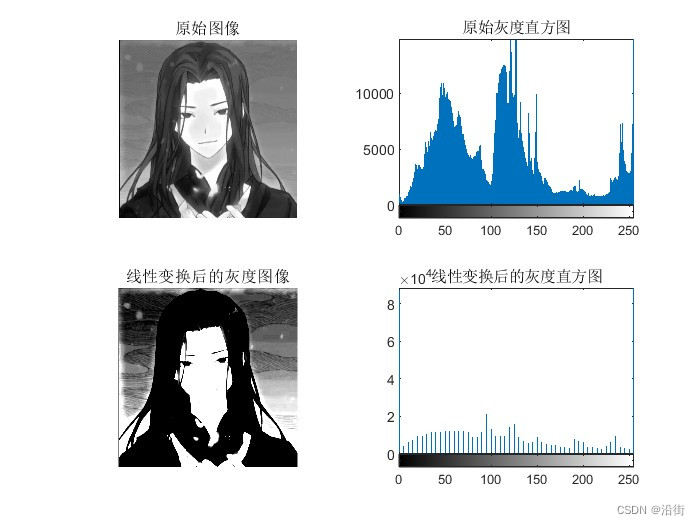
图1 线性变换与原始图像对比图
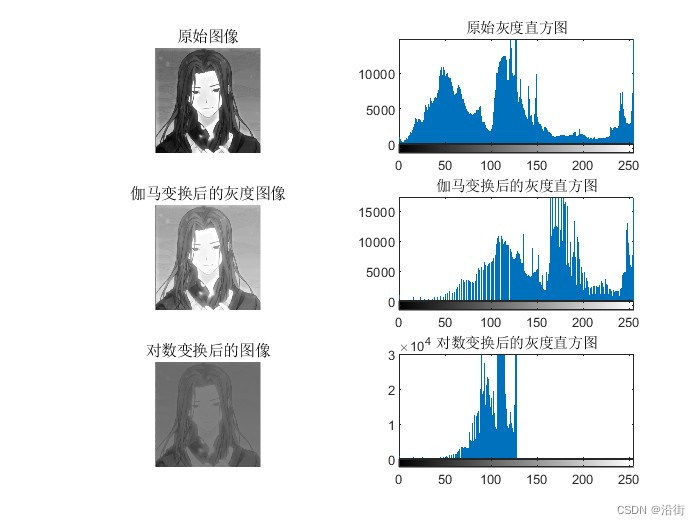
图2 非线性变换与原始图像对比图
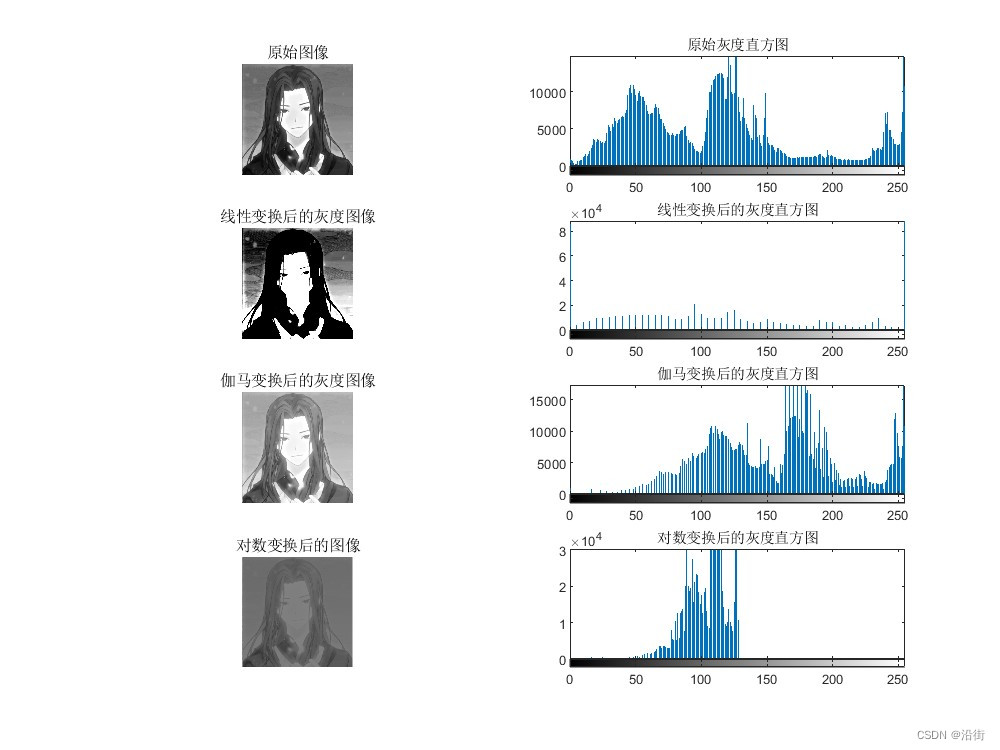
图3 总体变换对比图
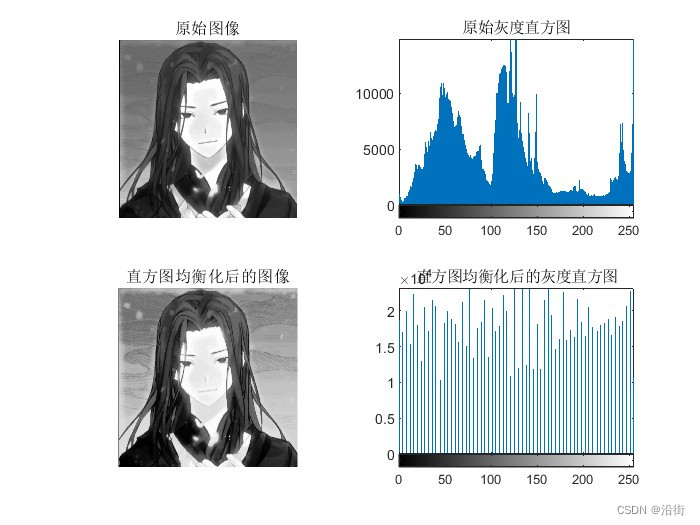
图4 直方图均衡化对比图