一、树定义
1、n个节点组成的具有层次结构的集合
2、每个节点有0个或多个子节点
3、每个非根节点只有一个父节点(根节点没有父节点 )
4、除根节点,每个子节点可以分成多个不相交的子树
概念定义:
节点深度 :节点到根节点的路径长度,称为这个节点的深度
节点高度 :
树深度:节点深度的最大值就是树的深度
父节点 :
子节点 :
兄弟节点 :拥有共同父节点
度:节点有多少个子节点称为这个节点的度
祖先:
后代:
森林:多个互不相交的树组合构成一个森林
树的分类:
无序树 :树的任意节点的子节点无顺序关系
有序树:树的任意节点的子节点有顺序关系
二叉树 :任意节点最多只有2个节点的树
代码:二叉树遍历
二叉树遍历分为:前序、中序、后续,以父节点的访问次序来区分的
c
# 待续二、二叉树
1、满二叉树
1、所有的叶子节点都在同一层
2、非叶子节点都有2个度(2个子节点)
二叉树的每个位置都是有节点的,是一个比较完美的情况
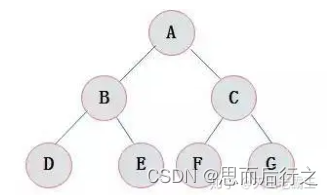
2、完全二叉树
1、除了树的最底层,所有的节点构成了满二叉树
2、最底层节点,从左到右紧密排列(最底层缺少的节点都在右边)
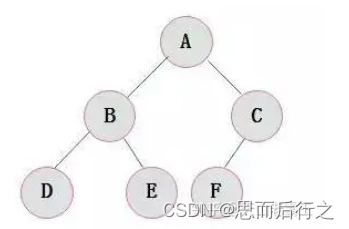
3、完满二叉树
1、除了叶子节点,其他节点都有且只有2子节点
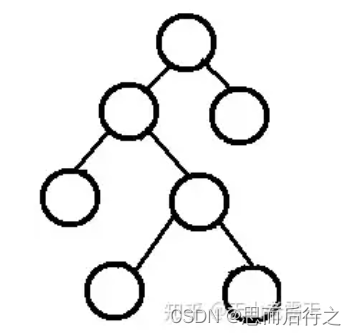
理解一下:以上三个二叉树,缺陷程度越来越大
4、二叉查找树
1、树的每个节点一定能分出大小
2、对于有子节点(左右节点至少有一个)的节点,大小排序一定是: 左 < 中 < 右
理解:是一个有序二叉树
5、平衡二叉树
1、对于每个节点的值而言,他是一个有序二叉树
2、对与树的结构而言,每个节点的子节点的高度差不大于1
6、红黑树
1、红黑树首先是一个二叉查找树(有序树)
2、节点是红色或者黑色,根节点固定地黑色
对于节点颜色的规则:
1、根节点固定是黑色
2、红节点的子节点都是黑色(结论:每个叶子节点到根节点,不存在连续的红节点)
3、叶子节点固定为黑色
4、任意节点到其所有叶子节点的路径都有同样数量的黑色。
红黑树使用场景
1、红黑树多用于搜索,插入,删除操作多的情况下
2、在C++的STL中。map和set都是用红黑树实现的
3、linux进程调度Completely Fair Scheduler,用红黑树管理进程控制块
4、epoll在内核中的实现,用红黑树管理事件块
5、nginx中,用红黑树管理timer