机器学习(V)--无监督学习(六)流形学习

流形学习

流形学习 （manifold learning）是一种借助拓扑流形概念的降维方法，流形是指在局部与欧式空间同胚的空间，即在局部与欧式空间具有相同的性质，能用欧氏距离计算样本之间的距离。这样即使高维空间的分布十分复杂，但是在局部上依然满足欧式空间的性质，基于流形学习的降维正是这种邻域保持的思想。

流形学习可以被认为是一种试图推广像PCA这样的线性框架，使其对数据中的非线性结构敏感。下面分别对几种著名的流行学习方法进行介绍。

给定样本矩阵

X = ( x 1 x 2 ⋯ x N ) = ( x 11 x 12 ⋯ x 1 N x 21 x 22 ⋯ x 2 N ⋮ ⋮ ⋱ ⋮ x p 1 x p 2 ⋯ x p N ) X=\begin{pmatrix}\mathbf x_1&\mathbf x_2&\cdots&\mathbf x_N\end{pmatrix}= \begin{pmatrix} x_{11}&x_{12}&\cdots&x_{1N} \\ x_{21}&x_{22}&\cdots&x_{2N} \\ \vdots&\vdots&\ddots&\vdots \\ x_{p1}&x_{p2}&\cdots&x_{pN} \\ \end{pmatrix} X=(x1x2⋯xN)=⎝⎜⎜⎜⎛x11x21⋮xp1x12x22⋮xp2⋯⋯⋱⋯x1Nx2N⋮xpN⎠⎟⎟⎟⎞

包含 N N N 个样本， p p p 个特征。其中，第 j j j 个样本的特征向量为 x j = ( x 1 j , x 2 j , ⋯ , x p j ) T \mathbf x_j=(x_{1j},x_{2j},\cdots,x_{pj})^T xj=(x1j,x2j,⋯,xpj)T 。

多维缩放

多维缩放（Multi-dimensional Scaling, MDS）也被称作 PCoA (Principal Coordinate Analysis)，是一种经典的降维算法，其原理是利用成对样本间的相似性，去构建合适的低维空间，这样才会使得原始空间样本之间的关系及总体分布不发生较大的改变。如果这个低维的空间是2维或者3维，则可以直观的可视化降维结果。

MDS 大致分为三类：

Classical MDS：经典 MDS 在低维空间使用欧式距离通过特征分解来寻找最优映射
Metric MDS：度量MDS在低维空间可以采用非欧式距离，使用迭代优化算法求解
Non-Metric MDS：度量MDS 在低维空间可以采用非度量距离，同样使用迭代优化算法求解

Classical MDS

假定 N N N个样本在原始空间中任意两两样本之间的距离矩阵为 D = ( δ i j ) N × N D=(\delta_{ij}){N\times N} D=(δij)N×N ，其中元素 δ i j \delta{ij} δij 表示原始空间第 i i i 个样本和第 j j j 个样本之间的距离。假设将样本映射到低维的 p ' p' p' 维空间中
Z = ( z 1 z 2 ⋯ z N ) Z=\begin{pmatrix}\mathbf z_1&\mathbf z_2&\cdots&\mathbf z_N\end{pmatrix} Z=(z1z2⋯zN)

元素 d i j d_{ij} dij 表示映射空间第 i i i 个样本和第 j j j 个样本之间的距离，原始的距离可以使用任何类型的距离矩阵，但低维近似通常表示欧式距离。我们在 MDS 中要实现的，就是对距离矩阵进行近似
δ i j ≈ d i j = ∥ z i − z j ∥ 2 \delta_{ij}\approx d_{ij}=\|\mathbf z_i-\mathbf z_j\|_2 δij≈dij=∥zi−zj∥2

注意到上述约束条件是没有唯一解的，因为平移或反转不改变欧式距离。因此我们并不直接求解降维结果 Z Z Z ，而是求解降维后样本的内积矩阵 S = Z T Z S=Z^TZ S=ZTZ，然后通过特征值分解的得到降维后的样本矩阵。

令元素 s i j = z i T z j s_{ij}=\mathbf z_i^T\mathbf z_j sij=ziTzj 表示映射空间第 i i i 个样本和第 j j j 个样本的内积。欧式距离对应于向量内积
δ i j 2 ≈ ∥ z i ∥ 2 + ∥ z j ∥ 2 − 2 z i T z j = s i i + s j j − 2 s i j \begin{aligned} \delta^2_{ij}&\approx \|\mathbf z_i\|^2+\|\mathbf z_j\|^2-2\mathbf z_i^T\mathbf z_j \\ &=s_{ii}+s_{jj}-2s_{ij} \end{aligned} δij2≈∥zi∥2+∥zj∥2−2ziTzj=sii+sjj−2sij

为方便讨论，考虑降维后的数据样本中心化，即
∑ i = 1 N z i = 0 \sum_{i=1}^N\mathbf z_i=0 i=1∑Nzi=0

显然，内积矩阵的各行与各列之和均为0（因为总能提速到样本加和），于是可以得到方程组
δ i j 2 = s i i + s j j − 2 s i j ∑ i = 1 N δ i j 2 = tr ( S ) + N s j j ∑ j = 1 N δ i j 2 = tr ( S ) + N s i i ∑ i = 1 N ∑ j = 1 N δ i j 2 = 2 N tr ( S ) \delta^2_{ij}=s_{ii}+s_{jj}-2s_{ij}\\ \sum_{i=1}^N\delta^2_{ij}=\text{tr}(S)+Ns_{jj} \\ \sum_{j=1}^N\delta^2_{ij}=\text{tr}(S)+Ns_{ii} \\ \sum_{i=1}^N\sum_{j=1}^N\delta^2_{ij}=2N\text{tr}(S) δij2=sii+sjj−2siji=1∑Nδij2=tr(S)+Nsjjj=1∑Nδij2=tr(S)+Nsiii=1∑Nj=1∑Nδij2=2Ntr(S)

最终求得
s i j = − 1 2 ( δ i j 2 − 1 N ∑ i = 1 N δ i j 2 − 1 N ∑ j = 1 N δ i j 2 − 1 N 2 ∑ i = 1 N ∑ j = 1 N δ i j 2 ) s_{ij}=-\frac{1}{2}\left(\delta^2_{ij}-\frac{1}{N}\sum_{i=1}^N\delta^2_{ij}-\frac{1}{N}\sum_{j=1}^N\delta^2_{ij}-\frac{1}{N^2} \sum_{i=1}^N\sum_{j=1}^N\delta^2_{ij}\right) sij=−21(δij2−N1i=1∑Nδij2−N1j=1∑Nδij2−N21i=1∑Nj=1∑Nδij2)

矩阵表达式为
S = − 1 2 C N D 2 C N S=-\frac{1}{2}C_ND^2C_N S=−21CND2CN

其中 D 2 = ( δ i j 2 ) N × N D^2=(\delta_{ij}^2){N\times N} D2=(δij2)N×N 是距离元素逐个的平方矩阵。中心化矩阵
C N = I N − 1 N 1 N × N C_N=I_N-\frac{1}{N}1{N\times N} CN=IN−N11N×N

其中 1 N × N 1_{N\times N} 1N×N 表示元素全为1的 N N N 阶方阵。

由于 S S S是正定实对称矩阵，只需对 S S S 进行特征值分解
S = V Λ V T S=V\Lambda V^T S=VΛVT

其中， Λ \Lambda Λ 是的特征值对角阵， V V V 是特征向量矩阵。为了降维，我们可以只保留前 p ′ p' p′ 个最大的特征值以及对应的特征向量，投影得到降维后的样本矩阵
Z = Λ V T Z=\sqrt \Lambda V^T Z=Λ VT

需要指出，这个解并不唯一。

具体来说，经典MDS算法的基本步骤如下：

Step 1 计算原始空间中每对数据点之间的距离来构建距离矩阵。

Step 2 通过距离矩阵，我们可以计算内积矩阵。

Step 3 对内积矩阵进行特征值分解。

Step 4 计算降维后的坐标。

Metric MDS

通常距离度量需满足以下基本性质:

非负性： d ( x i , x j ) ≥ 0 d(x_i,x_j)\geq 0 d(xi,xj)≥0
对称性： d ( x i , x j ) = d ( x j , x i ) d(x_i,x_j)=d(x_j,x_i) d(xi,xj)=d(xj,xi)
三角不等式： d ( x i , x j ) ≤ d ( x i , x k ) + d ( x k , x j ) d(x_i,x_j)\leq d(x_i,x_k)+d(x_k,x_j) d(xi,xj)≤d(xi,xk)+d(xk,xj)

如果满足三角不等式，则为度量距离（Metric distance）。低维近似使用度量距离的MDS称为度量MDS（Metric MDS），它基于最小二乘损失函数，也被称为最小二乘MDS（least squares scaling）。

通常，Metric MDS 最小化称为 stress （Standardized Residual Sum of Squares）的损失函数，来比较低维的距离和实际距离
S t r e s s = ∑ i < j ( d i j − δ i j ) 2 Stress=\sum_{i<j}(d_{ij}-\delta_{ij})^2 Stress=i<j∑(dij−δij)2

最终采用某种优化过程（例如，梯度下降法）来最小化误差。

原始 stress 函数对距离的比例尺非常敏感，为了克服这个问题，引入了归一化
S t r e s s = ∑ i < j ( d i j − δ i j ) 2 ∑ i < j d i j 2 Stress=\sqrt{\frac{\sum_{i<j}(d_{ij}-\delta_{ij})^2}{\sum_{i<j}d_{ij}^2}} Stress=∑i<jdij2∑i<j(dij−δij)2

然后，使用 SMACOF 来优化应力函数。在此，我们不讨论这些算法的细节。度量MDS典型的方法是以某种方式初始化低维空间的点（例如PCA），然后修正这些点，以降低应力。

Initialization: Initialize points in random positions
Compute distances: Obtain distance matrix for the configuration
Calculate Loss: Evaluate stress function
Optimize: Gradient descent to update minimize stress

Non-Metric MDS

许多距离很容易违反三角不等式，比如序数数据。非度量MDS （Non-Metric MDS）要实现的是对距离矩阵单调函数进行低维近似
d i j ≈ f ( δ i j ) d_{ij}\approx f(\delta_{ij}) dij≈f(δij)

其中 f f f 是一个单调函数，输出相同的顺序。损失函数
S t r e s s = ∑ i < j ( d i j − f ( δ i j ) ) 2 ∑ i < j d i j 2 Stress=\sqrt{\frac{\sum_{i<j}(d_{ij}-f(\delta_{ij}))^2}{\sum_{i<j}d_{ij}^2}} Stress=∑i<jdij2∑i<j(dij−f(δij))2

等距特征映射

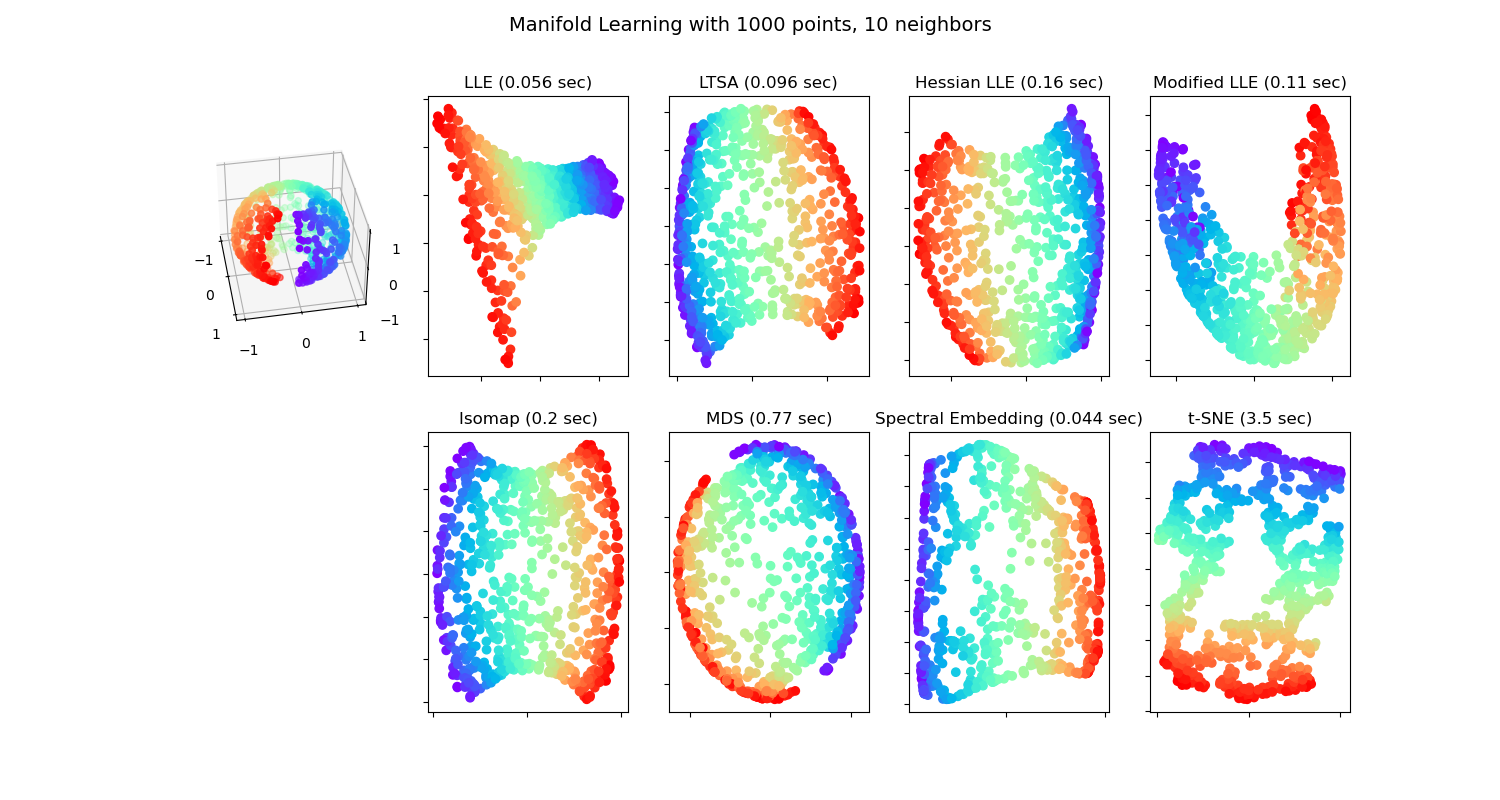
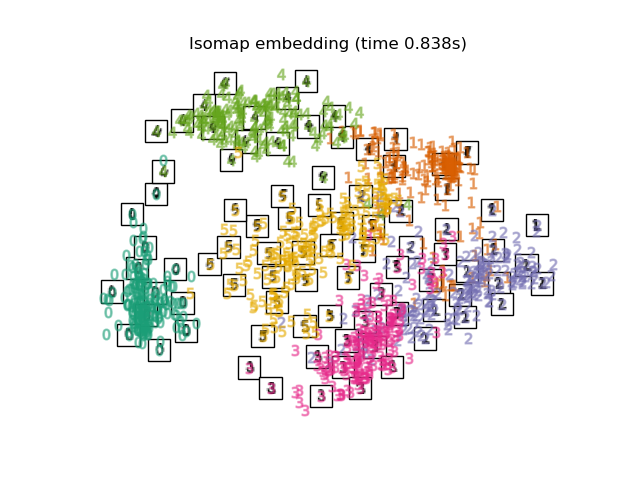
等距特征映射(isometric feature mapping, isomap)算法是最早的流形学习方法之一，核心思想是寻求一种更低维度的嵌入，以保持数据点之间的测地线距离（geodesic distance）。最终，对距离矩阵应用MDS，来得到低维映射。

任意两点的测地线距离则是利用流形在局部上与欧式空间同胚的性质，使用近邻欧式距离来逼近测地线距离。这样，高维空间中两个样本之间的距离就转为最短路径问题。可采用著名的Dijkstra算法 或Floyd算法计算最短距离。

Isomap的工作原理可以概括为以下几个步骤：

最近邻搜索 ：首先，为每个数据点找到其 k k k个最近邻，并在这些点之间构建一个邻接图。
最短路径图搜索：在邻接图中，计算所有点对之间的测地距离。这通常是通过Dijkstra算法或Floyd-Warshall算法来完成的。
构建距离矩阵：基于测地距离，构建一个距离矩阵，其中每个元素表示两个数据点之间的测地距离。
多维缩放（MDS）：使用MDS 技术将距离矩阵转换为低维空间中的点的坐标。

局部线性嵌入

LLE

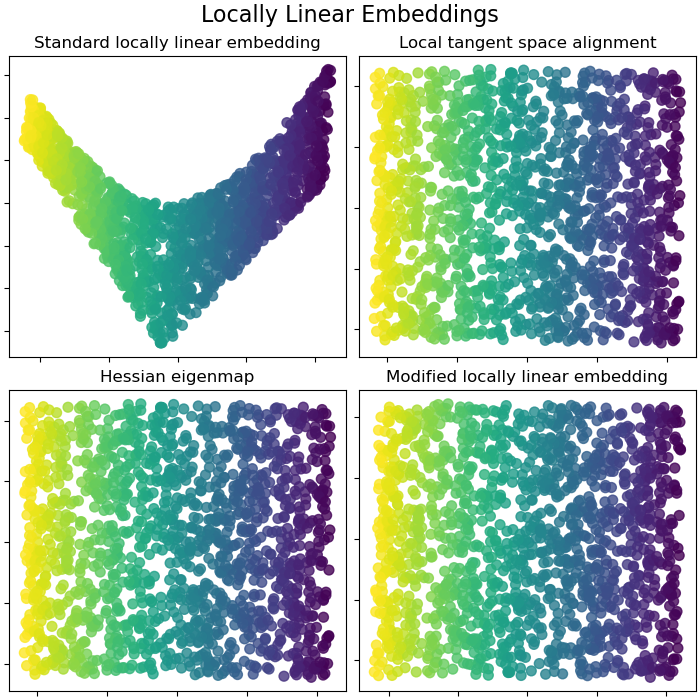
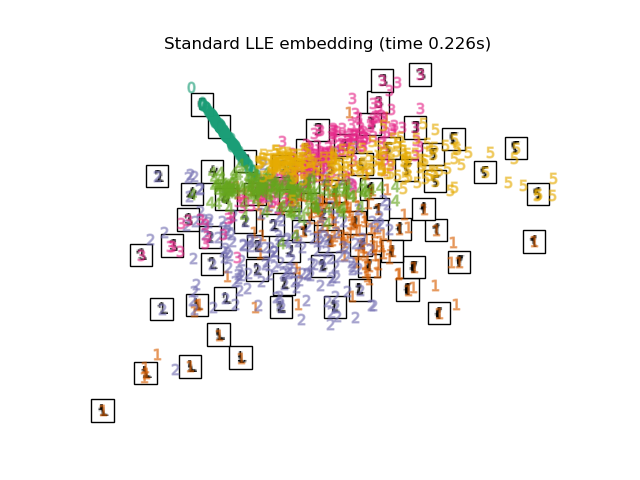
局部线性嵌入(Local linear embedding, LLE)不同与 ISOMAP 考虑全局连接信息，LLE试图在降维前后保持邻域内样本之间的线性关系。

假定原始空间样本 x i \mathbf x_i xi可以通过它的邻域样本集 N ( i ) \mathcal N(i) N(i) 线性表出：
x i = ∑ k ∈ N ( i ) w i k x k \mathbf x_i= \sum_{k\in \mathcal N(i)}w_{ik}\mathbf x_k xi=k∈N(i)∑wikxk

那么LLE算法认为在低维空间同样应该保持上述线性关系：
z i ≈ ∑ k ∈ N ( i ) w i k z k \mathbf z_i\approx \sum_{k\in \mathcal N(i)}w_{ik}\mathbf z_k zi≈k∈N(i)∑wikzk

所以LLE算法的核心就是如何根据高维空间的邻域线性关系求解具有同邻域线性关系的低维流形嵌入。

LLE算法大致分为以下几步：

Step 1 ：寻找每个样本 x i x_i xi欧式距离下的 K K K近邻点 N ( i ) \mathcal N(i) N(i)，邻域矩阵记作
N i = ( x i k ) p × K , k ∈ N ( i ) N_i=(x_{ik})_{p\times K},\quad k\in \mathcal N(i) Ni=(xik)p×K,k∈N(i)

Step 2 ：根据 K K K近邻点计算出每个样本的邻域重构系数 w i \mathbf w_i wi 。这显然是个回归问题，我们最小化均方误差
min ⁡ W ∑ i = 1 N ∥ x i − ∑ k ∈ N ( i ) w i k x k ∥ 2 2 s.t. ∑ k ∈ N ( i ) w i k = 1 \min_{W}\sum_{i=1}^N\|\mathbf x_i-\sum_{k\in \mathcal N(i)}w_{ik}\mathbf x_k\|2^2 \\ \text{s.t. }\sum{k\in \mathcal N(i)}w_{ik}=1 Wmini=1∑N∥xi−k∈N(i)∑wikxk∥22s.t. k∈N(i)∑wik=1

为方便计算，一般我们也会对权重系数做归一化的限制。损失函数
J ( W ) = ∑ i = 1 N ∥ x i − ∑ k ∈ N ( i ) w i k x k ∥ 2 2 = ∑ i = 1 N ∥ x i − N i w i ∥ 2 2 = ∑ i = 1 N ∥ ( x i 1 K T − N i ) w i ∥ 2 2 = ∑ i = 1 N w i T C i w i \begin{aligned} J(W)&=\sum_{i=1}^N\|\mathbf x_i-\sum_{k\in \mathcal N(i)}w_{ik}\mathbf x_k\|2^2 \\ &=\sum{i=1}^N\|\mathbf x_i-N_i\mathbf w_i\|2^2 \\ &=\sum{i=1}^N\|(\mathbf x_i 1_K^T-N_i)\mathbf w_i\|2^2 \\ &=\sum{i=1}^N\mathbf w_i^TC_i \mathbf w_i \end{aligned} J(W)=i=1∑N∥xi−k∈N(i)∑wikxk∥22=i=1∑N∥xi−Niwi∥22=i=1∑N∥(xi1KT−Ni)wi∥22=i=1∑NwiTCiwi

其中 C i = ( x i 1 K T − N i ) T ( x i 1 K T − N i ) ∈ R K × k C_i=(\mathbf x_i 1_K^T-N_i)^T(\mathbf x_i 1_K^T-N_i)\in \R^{K\times k} Ci=(xi1KT−Ni)T(xi1KT−Ni)∈RK×k 已知。则上述优化目标可重写为
min ⁡ W ∑ i = 1 N w i T C i w i s.t. w i T 1 K = 1 \min_{W}\sum_{i=1}^N\mathbf w_i^TC_i \mathbf w_i\\ \text{s.t. }\mathbf w_i^T 1_K=1 Wmini=1∑NwiTCiwis.t. wiT1K=1

使用拉格朗日乘子法可以求出
w i = C i − 1 1 K 1 K T C i − 1 1 K \mathbf w_i=\frac{C_i^{-1}1_K}{1_K^TC_i^{-1}1_K} wi=1KTCi−11KCi−11K

其中，分母是为了让权重系数归一化。另外，为了后续方便使用，我们把系数 w i \mathbf w_i wi充到 N N N维，对于不属于邻域内的点设置为0：
w i k = 0 , if k ∉ N ( i ) w_{ik}=0, \quad\text{if }k\not\in \mathcal N(i) wik=0,if k∈N(i)

至此，已求得 N × N N\times N N×N维权重系数矩阵
W = ( w 1 w 2 ⋯ w N ) W=\begin{pmatrix}\mathbf w_1&\mathbf w_2&\cdots&\mathbf w_N\end{pmatrix} W=(w1w2⋯wN)

Step 3 ：最后，在低维空间中保持 w i \mathbf w_i wi不变，最小化损失函数来求解低维坐标矩阵 Z Z Z。
J ( Z ) = ∑ i = 1 N ∥ z i − ∑ k ∈ N ( i ) w i k z k ∥ 2 2 = ∥ Z ( I − W ) ∥ 2 2 = tr ( Z M Z T ) \begin{aligned} J(Z)&=\sum_{i=1}^N\|\mathbf z_i-\sum_{k\in \mathcal N(i)}w_{ik}\mathbf z_k\|_2^2 \\ &=\|Z(I-W)\|_2^2 \\ &=\text{tr}(ZMZ^T) \end{aligned} J(Z)=i=1∑N∥zi−k∈N(i)∑wikzk∥22=∥Z(I−W)∥22=tr(ZMZT)

其中 M = ( I − W ) ( I − W ) T M=(I-W)(I-W)^T M=(I−W)(I−W)T。^1^

一般我们也会加入中心化和协方差限制条件：
∑ i = 1 N z i = 0 ∑ i = 1 N z i z i T = I \sum_{i=1}^N\mathbf z_i=0 \\ \sum_{i=1}^N\mathbf z_i\mathbf z_i^T=I i=1∑Nzi=0i=1∑NziziT=I

这样优化问题可以重写为矩阵形式：^2^
min ⁡ Z tr ( Z M Z T ) s.t. Z Z T = I \min_Z\text{tr}(ZMZ^T) \\ \text{s.t. }ZZ^T=I Zmintr(ZMZT)s.t. ZZT=I

使用拉格朗日乘子法，可以得到
M Z T = Z T Λ MZ^T= Z^T\Lambda MZT=ZTΛ

这是一个矩阵特征值分解问题， Λ = diag ( λ 1 , λ 2 , ⋯ , λ p ) \Lambda=\text{diag}( \lambda_1 ,\lambda_2, \cdots ,\lambda_p) Λ=diag(λ1,λ2,⋯,λp)的对角元素就是矩阵 M M M的特征值。我们的损失函数变为
tr ( Z M Z T ) = tr ( Z Z T Λ ) = tr ( Λ ) = ∑ i = 1 N λ i \text{tr}(ZMZ^T)=\text{tr}(ZZ^T\Lambda)=\text{tr}(\Lambda)=\sum_{i=1}^N\lambda_i tr(ZMZT)=tr(ZZTΛ)=tr(Λ)=i=1∑Nλi

于是，要取得降维后的最小损失函数，只需对矩阵 M M M 进行特征值分解，再取最小的 p ′ p' p′ 个特征值对应的特征向量组成 Z T Z^T ZT

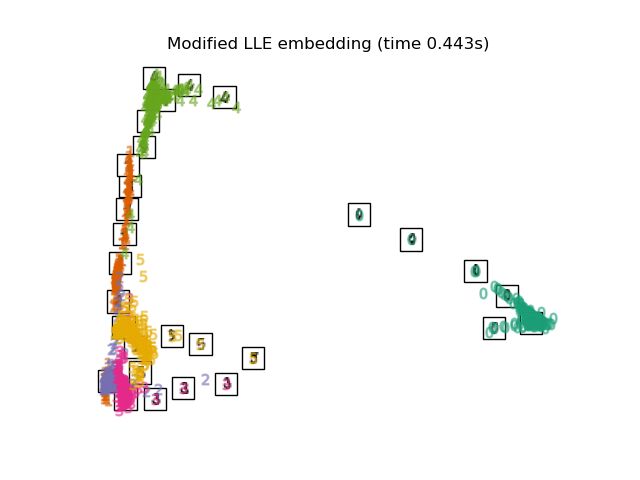
MLLE

Modified Locally Linear Embedding(MLLE) 希望找到的近邻的分布权重尽量在样本的各个方向，而不是集中在一侧。

HLLE

Hessian Eigenmapping 也称 Hessian Based LLE(HLLE)，希望保持局部Hessian矩阵二次曲面关系而非线性关系。

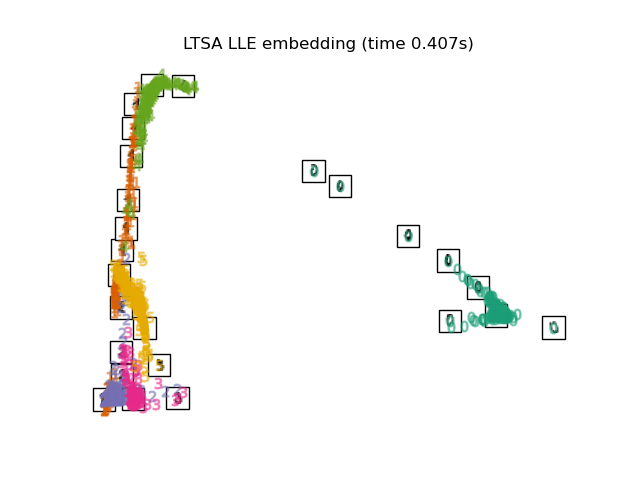
LTSA

Local tangent space alignment(LTSA) 虽然从技术上讲不是 LLE 的变体，但在算法上与 LLE 非常相似，可以将其归入此类别。 LTSA希望保持数据集局部的几何关系，同时利用了局部几何到整体性质过渡的技巧。

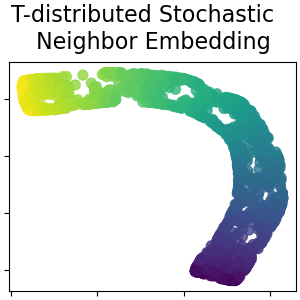
t-SNE

SNE

随机邻域嵌入(Stochastic Neighbor Embedding)是一种非线性降维算法，主要用于高维数据降维到2维或者3维，进行可视化。例如，当我们想对高维数据集进行分类，但又不清楚这个数据集有没有很好的可分性（同类之间间隔小、异类之间间隔大）时，可以通过降维算法将数据投影到二维或三维空间中。t-SNE是由SNE发展而来。我们先介绍SNE的基本原理，之后再扩展到t-SNE。

相似度：SNE是通过将高维数据点间的距离关系转换为条件概率来表示相似性，并在低维空间中尽量保持这些相似度。

对于高维空间中的点 x i \mathbf x_i xi，以它为中心构建方差为 σ i \sigma_i σi 的高斯分布。条件概率 p j ∣ i p_ {j | i} pj∣i 表示 x j \mathbf x_j xj 在 x i \mathbf x_i xi 邻域的概率，若 x j \mathbf x_j xj 与 x i \mathbf x_i xi 相距很近，那么 p j ∣ i p_ {j | i} pj∣i 很大；反之， p j ∣ i p_ {j | i} pj∣i 很小。
p j ∣ i = exp ⁡ ( − ∥ x i − x j ∥ 2 / ( 2 σ i 2 ) ) ∑ k ≠ i exp ⁡ ( − ∥ x i − x k ∥ 2 / ( 2 σ i 2 ) ) p_ {j | i} = \frac{\exp(- \| \mathbf x_i -\mathbf x_j \| ^2 / (2 \sigma^2_i ))} {\sum_{k \neq i} \exp(- \| \mathbf x_i -\mathbf x_k\| ^2 / (2 \sigma^2_i))} pj∣i=∑k=iexp(−∥xi−xk∥2/(2σi2))exp(−∥xi−xj∥2/(2σi2))

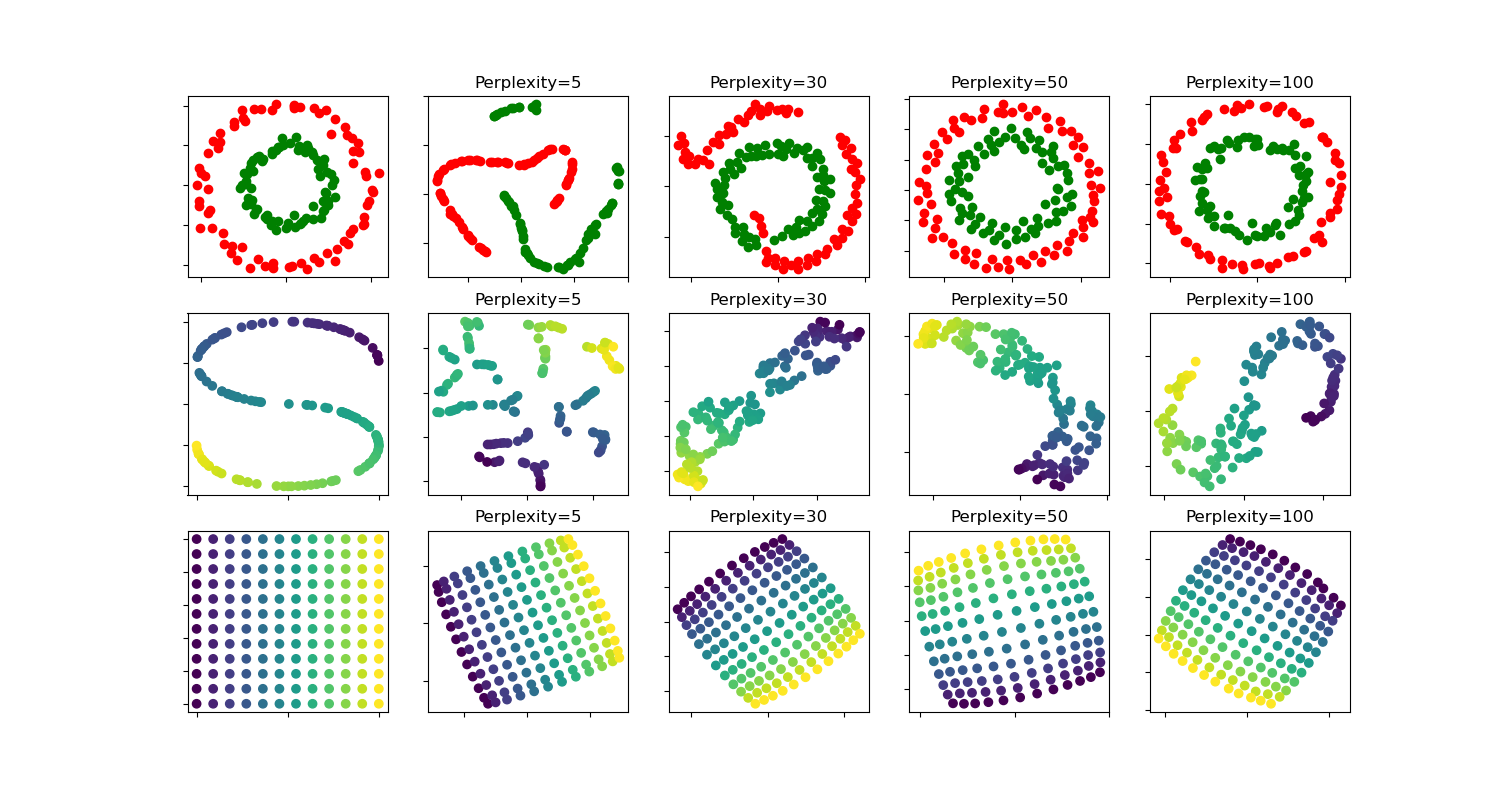
困惑度 ：(perplexity)因为低维空间中很难保留所有全局距离，因此SNE只关注每个数据点的局部邻居，而条件概率中的方差 σ i \sigma_i σi 决定了高斯分布的宽度，即圈选邻域的大小。不同点 x i \mathbf x_i xi的方差取值是不一样，在数据较为密集的区域中，更小的 σ i \sigma_i σi 值更为合适。在SNE中是通过超参数困惑度来系统调整方差的：
P e r p ( P i ) = 2 H ( P i ) Perp(P_i)=2^{H(P_i)} Perp(Pi)=2H(Pi)

其中 H ( P i ) H(P_i) H(Pi)为点 i i i的邻域概率， H ( P i ) H(P_i) H(Pi)是 P i P_i Pi的熵，即:
H ( P i ) = − ∑ j p j ∣ i log ⁡ 2 p j ∣ i H(P_i) = -\sum_j p_{j | i} \log_2 p_{j | i} H(Pi)=−j∑pj∣ilog2pj∣i

困惑度通过将熵(entropy)作为指数，等价于在匹配每个点的原始和拟合分布时考虑的最近邻数，较低的困惑度意味着我们在匹配原分布并拟合每一个数据点到目标分布时只考虑最近的几个最近邻，而较高的困惑度意味着拥有较大的「全局观」。在 SNE 和 t-SNE 中，困惑度是我们设置的参数（通常为 5 到 50 间）。

最常用的方法是二分搜索方差 σ i \sigma_i σi ，尽快适应设定的困惑度值。

目标函数 ：最后我们通过高低维度概率分布间的KL散度来衡量两个分布之间的相似性。
C = ∑ i ∑ j p j ∣ i log ⁡ p j ∣ i q j ∣ i C = \sum_i \sum_j p_{j | i} \log \frac{p_{j | i}}{q_{j | i}} C=i∑j∑pj∣ilogqj∣ipj∣i

低维度空间下的点 z i \mathbf z_i zi的条件概率
q j ∣ i = exp ⁡ ( − ∥ z i − z j ∥ 2 ) ∑ k ≠ i exp ⁡ ( − ∥ z i − z k ∥ 2 ) q_ {j | i} = \frac{\exp(- \| \mathbf z_i -\mathbf z_j \| ^2 )} {\sum_{k \neq i} \exp(- \| \mathbf z_i -\mathbf z_k\| ^2 )} qj∣i=∑k=iexp(−∥zi−zk∥2)exp(−∥zi−zj∥2)

这里为方便计算，直接设置方差 2 σ i 2 = 1 2\sigma^2_i=1 2σi2=1

然后使用梯度下降法来迭代更新
∂ C ∂ z i = 2 ∑ j ( p j ∣ i -- q j ∣ i + p i ∣ j -- q i ∣ j ) ( z i -- z j ) \frac{\partial C}{\partial\mathbf z_i} = 2 \sum_j (p_{j | i} -- q_{j | i} + p_{i | j} -- q_{i | j})(\mathbf z_i -- \mathbf z_j) ∂zi∂C=2j∑(pj∣i--qj∣i+pi∣j--qi∣j)(zi--zj)

需要注意的是KL散度是一个非对称的度量，高维空间中两个数据点距离较近时，若映射到低维空间后距离较远，那么将得到一个很高的惩罚。反之，高维空间中两个数据点距离较远时，若映射到低维空间距离较近，将得到一个很低的惩罚值。因此，SNE会倾向于保留数据中的局部特征。

SNE Algorithm

Initialize points randomly / with PCA
Compute pairwise distances
Convert distances to conditional probabilities
Perform binary search to find o that matches the desired perplexity
Optimize KL divergence for each point via gradient descent

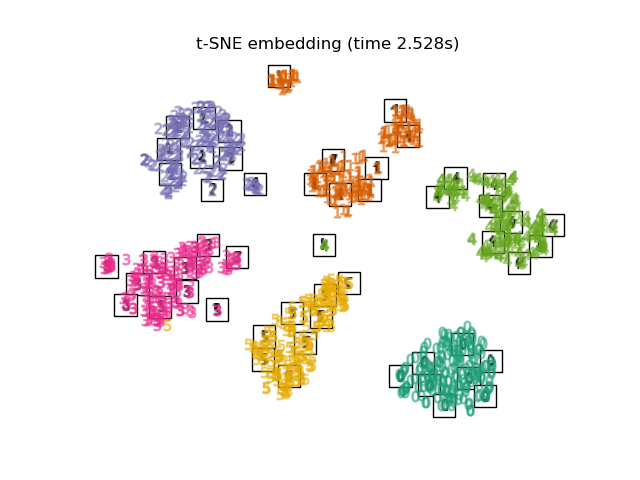
t-SNE

简单来说，t-SNE(t-distributed Stochastic Neighbor Embedding) 只是在SNE基础上进行了一些改进，但其核心算法保持不变。

拥挤问题：(Crowding)我们先来了解下拥挤问题，即不同类别的簇挤在一起，无法区分开来。拥挤问题与某个特定算法无关，而是由于高维空间距离分布和低维空间距离分布的差异造成的。想象下在一个三维的球里面有均匀分布的点，不难想象，如果把这些点投影到一个二维的圆上一定会有很多点是重合的。

t 分布：减轻拥挤问题的一个方法是在低维空间下，引入t分布来将距离转换为概率分布。与高斯分布相比， t 分布有较长的尾部，这有助于数据点在二维空间中更均匀地分布。

对称 SNE ：(Symmetric SNE)采用联合概率分布代替原始的条件概率，使得
p i j = p j i , q i j = q j i p_{ij} = p_{ji} ,\quad q_{ij}= q_{ji} pij=pji,qij=qji

目标函数为
C = ∑ i ∑ j p i j log ⁡ p i j q i j C = \sum_i \sum_j p_{ij} \log \frac{p_{ij}}{q_{ij}} C=i∑j∑pijlogqijpij

这种表达方式，使得整体简洁了很多，但是会引入异常值的问题。在高维空间中，离群值总在其它点的邻域内有较低的概率，因此它并没有被纳入代价函数考虑，为此作者建议在高维空间取联合概率
p i j = p j i = p j ∣ i + p i ∣ j 2 N p_{ij} = p_{ji} = \frac{p_{j | i} +p_{i | j} }{2N} pij=pji=2Npj∣i+pi∣j

在低维空间下，使用自由度为 1 的 t 分布重新定义概率
q i j = q j i = ( 1 + ∥ z i − z j ∥ 2 ) − 1 ∑ k ≠ l ( 1 + ∥ z k − z l ∥ 2 ) − 1 q_{ij}=q_{ji} = \frac{(1 + \|\mathbf z_i -\mathbf z_j \| ^2)^{-1}}{\sum_{k \neq l} (1 + \| \mathbf z_k -\mathbf z_l \| ^2)^{-1}} qij=qji=∑k=l(1+∥zk−zl∥2)−1(1+∥zi−zj∥2)−1

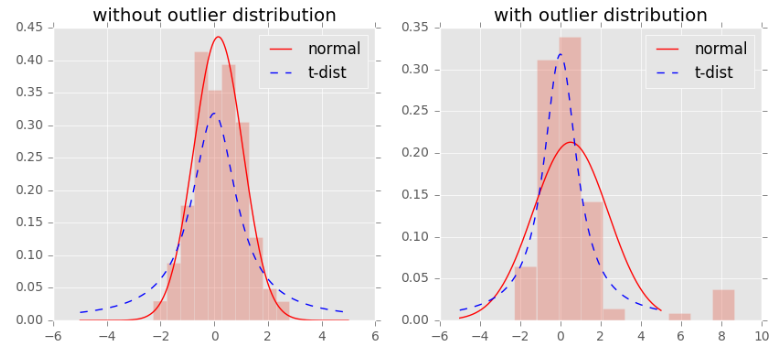
如上图，t分布受异常值影响更小，拟合结果更为合理，较好的捕获了数据的整体特征。

修正概率分布之后的梯度
∂ C ∂ z i = 4 ∑ j ( p i j -- q i j ) ( z i -- z j ) ( 1 + ∥ z i -- z j ∥ 2 ) − 1 \frac{\partial C}{\partial\mathbf z_i} = 4 \sum_j (p_{ij} -- q_{ij} )(\mathbf z_i -- \mathbf z_j)(1+\|\mathbf z_i -- \mathbf z_j\|^2)^{-1} ∂zi∂C=4j∑(pij--qij)(zi--zj)(1+∥zi--zj∥2)−1

早期夸大策略 ：(early exaggeration)在开始优化阶段， p i j p_{ij} pij乘以一个大于1的数进行扩大，来避免因为 q i j q_{ij} qij太小导致优化太慢的问题。比如前50次迭代， p i j p_{ij} pij乘以4。

Barnes-Hut t-SNE

Barnes-Hut t-SNE 是一种高效的降维算法，适用于处理大规模数据集，是 t-SNE 的一个变体。这种算法主要被用来可视化高维数据，并帮助揭示数据中的内部结构。

在处理大型数据集时，直接计算所有点对之间的相互作用非常耗时。Barnes-Hut t-SNE 采用了在天体物理学中常用的 Barnes-Hut 算法来优化计算过程。这种算法最初是为了解决 N体问题（即计算多个物体之间相互作用的问题）而设计的，算法加入了空间划分的数据结构，以降低点之间相互作用的复杂性。

Barnes-Hut 算法通过以下步骤优化这个过程：

构建空间索引树：在二维空间中构建四叉树，在三维空间中构建八叉树。每个节点表示一个数据点，而每个内部节点则表示它的子节点的质心（即子节点的平均位置）。
近似相互作用：在计算点之间的作用力（即梯度下降中的梯度）时，Barnes-Hut 算法不是计算每一对点之间的相互作用，而是使用树来估计远距离的影响。对于每个点，如果一个节点（或其包含的数据点的区域）距离足够远（根据预设的阈值，如节点的宽度与距离的比率），则该节点内的所有点可以被视为一个单一的质心，从而简化计算。
有效的梯度计算：通过这种近似，算法只需要计算与目标点近邻的实际点以及远处质心的影响，极大地减少了必须执行的计算量。

通过这种方法，Barnes-Hut t-SNE 将复杂度从 O ( N 2 ) O(N^2) O(N2) 降低到 O ( N log ⁡ ⁡ N ) O(N\log ⁡N) O(Nlog⁡N)，使其能够有效地处理数万到数十万级别的数据点。但是这种效率的提升是以牺牲一定的精确度为代价的，因为远距离的相互作用是通过质心近似来实现的，而不是精确计算。

UAMP

UMAP(Uniform Manifold Approximation and Projection)直译为均匀流形近似和投影，它是一种基于数学拓扑流形的方法，用于将高维数据映射到低维空间，以便于可视化和分析。

UMAP的思路和t-SNE很相似，主要通过以下几个方程构建。

条件概率 ：在高维空间使用指数概率分布
p j ∣ i = exp ⁡ ( − max ⁡ { 0 , d ( x i , x j } − ρ i ) σ i ) p_{j|i}=\exp(-\frac{\max\{0,d(\mathbf x_i,\mathbf x_j\}-\rho_i)}{\sigma_i}) pj∣i=exp(−σimax{0,d(xi,xj}−ρi))

其中 ρ i \rho_i ρi 是数据点 x i \mathbf x_i xi第一个最近邻居的距离
ρ i = min ⁡ d ( x i , x j ) , 1 ≤ j ≤ K \rho_i=\min d(\mathbf x_i,\mathbf x_j),\quad 1\le j \le K ρi=mind(xi,xj),1≤j≤K

这样可以确保流形的本地连通性，从第一个邻居之后条件概率开始指数衰减。

邻域大小 ：与t-SNE使用困惑度不同，UMAP直接使用了最近邻居的数量来搜索 σ i \sigma_i σi，最终定义每个点周围邻域的半径
∑ j p j ∣ i = log ⁡ 2 K \sum_jp_{j|i}=\log_2K j∑pj∣i=log2K

概率对称

高维空间基于拓扑学定理
p i j = p j ∣ i + p i ∣ j − p j ∣ i p i ∣ j p_{ij}=p_{j | i} +p_{i | j}-p_{j | i} p_{i | j} pij=pj∣i+pi∣j−pj∣ipi∣j

低维空间使用了和 t分布非常相似的曲线簇
q i j = ( 1 + a ( z i − z j ) 2 b ) − 1 q_{ij}=(1+a(\mathbf z_i-\mathbf z_j)^{2b})^{-1} qij=(1+a(zi−zj)2b)−1

目标优化 ：使用交叉熵（CE）作为损失函数
C E ( X , Z ) = ∑ i ∑ j [ p i j log ⁡ p i j q i j + ( 1 − p i j ) log ⁡ 1 − p i j 1 − q i j ] CE(X,Z) = \sum_i \sum_j\left[ p_{ij} \log \frac{p_{ij}}{q_{ij}} + (1-p_{ij} )\log \frac{1-p_{ij}}{1-q_{ij}}\right] CE(X,Z)=i∑j∑[pijlogqijpij+(1−pij)log1−qij1−pij]

使用随机梯度下降迭代更新。

拉普拉斯特征映射

拉普拉斯特征映射(Laplacian Eigenmaps)是一种基于图的降维算法，它希望在原空间中相互间有相似关系的点，在降维后的空间中尽可能的靠近。

拉普拉斯特征映射在sklearn流形学习中被叫做谱嵌入(Spectral Embedding)。

邻接矩阵

在图嵌入中，衡量两个点是否相似的最直接度量为构建邻接矩阵(Adjacent Matrix)，也称为相似矩阵(Similarity Matrix)或亲和矩阵(Affinity Matrix)。

无向图 ：如果两个数据点 x i \mathbf x_i xi 和 x j \mathbf x_j xj是邻近点，则在它们之间形成一条边作为连接关系。判断近邻关系的原则通常有以下三种：

ϵ \epsilon ϵ近邻法：预先设定一个阈值，若距离满足 ∥ x i − x j ∥ ≤ ϵ \|\mathbf x_i-\mathbf x_j\|\le\epsilon ∥xi−xj∥≤ϵ则用边进行连接。该方法基于几何距离信息，建立的连接关系是自然对称的，但阈值的选取往往是困难的，容易出现连接关系混乱。
K K K近邻法：取每个点附近的 K K K个点作为邻近点建立连接关系。该方法便于实现，所建立的连接关系是对称的，但是缺乏几何直观性。
全连接法：直接建立所有点之间的连接关系，该方法最为直接，但会对后续的计算过程造成不便。

邻接矩阵 ：在具有连接关系的两点 x i \mathbf x_i xi 和 x j \mathbf x_j xj 之间的边上赋予权重，得到图的相似矩阵 W W W 。通常有两种方式：

简单形式(simple-minded)

w i j = { 1 , if connected 0 , otherwise w_{ij}=\begin{cases} 1, & \text{if connected} \\ 0, & \text{otherwise} \end{cases} wij={1,0,if connectedotherwise

热核函数(heat kernel)

w i j = { exp ⁡ ( − ∥ z i − z j ∥ 2 / t ) , if connected 0 , otherwise w_{ij}=\begin{cases} \exp(-\|\mathbf z_i-\mathbf z_j\|^2/t ), & \text{if connected} \\ 0, & \text{otherwise} \end{cases} wij={exp(−∥zi−zj∥2/t),0,if connectedotherwise

显然， W W W是实对称矩阵。

优化目标

假设样本映射到低维空间中的数据矩阵为
Z = ( z 1 z 2 ⋯ z N ) Z=\begin{pmatrix}\mathbf z_1&\mathbf z_2&\cdots&\mathbf z_N\end{pmatrix} Z=(z1z2⋯zN)

优化目标
min ⁡ Z ∑ i = 1 N ∑ j = 1 N ∥ z i − z j ∥ 2 w i j \min_{Z}\sum_{i=1}^N\sum_{j=1}^N\|\mathbf z_i-\mathbf z_j\|^2w_{ij} Zmini=1∑Nj=1∑N∥zi−zj∥2wij

其中 w i j w_{ij} wij 为邻接矩阵 W W W的元素，距离较远的两点之间的边权重较小，而距离较近的两点间边的权重较大。

接下来对损失函数进行化简
J ( Z ) = ∑ i = 1 N ∑ j = 1 N ∥ z i − z j ∥ 2 w i j = ∑ i = 1 N ∑ j = 1 N ( z i T z i − 2 z i T z j + z j T z j ) w i j = ∑ i = 1 N ( ∑ j = 1 N w i j ) z i T z i − 2 ∑ i = 1 N ∑ j = 1 N w i j z i T z j + ∑ j = 1 N ( ∑ i = 1 N w i j ) z j T z j = ∑ i = 1 N d i z i T z i + ∑ j = 1 N d j z j T z j − 2 ∑ i = 1 N ∑ j = 1 N w i j z i T z j = 2 tr ( Z D Z T ) − 2 tr ( Z W Z T ) = 2 tr ( Z ( D − W ) Z T ) = 2 tr ( Z L Z T ) \begin{aligned} J(Z)&=\sum_{i=1}^N\sum_{j=1}^N\|\mathbf z_i-\mathbf z_j\|^2w_{ij} \\ &=\sum_{i=1}^N\sum_{j=1}^N(\mathbf z_i^T\mathbf z_i-2\mathbf z_i^T\mathbf z_j+\mathbf z_j^T\mathbf z_j)w_{ij} \\ &=\sum_{i=1}^N(\sum_{j=1}^Nw_{ij} )\mathbf z_i^T\mathbf z_i-2\sum_{i=1}^N\sum_{j=1}^Nw_{ij} \mathbf z_i^T\mathbf z_j+\sum_{j=1}^N(\sum_{i=1}^Nw_{ij} )\mathbf z_j^T\mathbf z_j \\ &=\sum_{i=1}^Nd_i\mathbf z_i^T\mathbf z_i+\sum_{j=1}^Nd_j\mathbf z_j^T\mathbf z_j-2\sum_{i=1}^N\sum_{j=1}^Nw_{ij} \mathbf z_i^T\mathbf z_j \\ &=2\text{tr}(ZDZ^T)-2\text{tr}(ZWZ^T) \\ &=2\text{tr}(Z(D-W)Z^T) \\ &=2\text{tr}(ZLZ^T) \end{aligned} J(Z)=i=1∑Nj=1∑N∥zi−zj∥2wij=i=1∑Nj=1∑N(ziTzi−2ziTzj+zjTzj)wij=i=1∑N(j=1∑Nwij)ziTzi−2i=1∑Nj=1∑NwijziTzj+j=1∑N(i=1∑Nwij)zjTzj=i=1∑NdiziTzi+j=1∑NdjzjTzj−2i=1∑Nj=1∑NwijziTzj=2tr(ZDZT)−2tr(ZWZT)=2tr(Z(D−W)ZT)=2tr(ZLZT)

其中矩阵
D = diag ( d 1 , d 2 , ⋯ , d N ) D=\text{diag}(d_1,d_2,\cdots,d_N) D=diag(d1,d2,⋯,dN)

是无向图的度矩阵 (Degree Matrix)，是对角阵。对角元素分别对应邻接矩阵各行之和
d i = ∑ i = 1 N w i j d_{i}=\sum_{i=1}^Nw_{ij} di=i=1∑Nwij

矩阵
L = D − M L=D-M L=D−M

是无向图的拉普拉斯矩阵(Laplacian Matrix)，是实对称阵。

至此优化问题可以重写为矩阵形式：
min ⁡ Z tr ( Z L Z T ) s.t. Z D Z T = I \min_Z\text{tr}(ZLZ^T) \\ \text{s.t. }ZDZ^T=I Zmintr(ZLZT)s.t. ZDZT=I

我们也会加入标准化条件获取唯一解。

广义特征值分解

使用拉格朗日乘子法求解优化目标，可以得到
L Z T = D Z T Λ LZ^T=DZ^T\Lambda LZT=DZTΛ

这是一个广义特征值分解问题， Λ = diag ( λ 1 , λ 2 , ⋯ , λ p ) \Lambda=\text{diag}( \lambda_1 ,\lambda_2, \cdots ,\lambda_p) Λ=diag(λ1,λ2,⋯,λp)的对角元素就是矩阵 L L L的相对于矩阵 D D D特征值。我们的损失函数变为
tr ( Z L Z T ) = tr ( Z D Z T Λ ) = tr ( Λ ) = ∑ i = 1 p λ i \text{tr}(ZLZ^T)=\text{tr}(ZDZ^T\Lambda)=\text{tr}(\Lambda)=\sum_{i=1}^p\lambda_i tr(ZLZT)=tr(ZDZTΛ)=tr(Λ)=i=1∑pλi

于是，要取得降维后的最小损失函数，只需对矩阵 L L L 进行广义特征值分解，再取最小的 p ′ p' p′ 个非零特征值对应的特征向量组成 Z T Z^T ZT

上式中用到了矩阵迹的性质： ∑ i a i T a i = tr ( A T A ) = tr ( A A T ) \sum_{i}a_i^Ta_i=\text{tr}(A^TA)=\text{tr}(AA^T) ∑iaiTai=tr(ATA)=tr(AAT) ↩︎
tr ( ∂ X A X T ) ∂ X = X ( A + A T ) \frac{\text{tr}(\partial XAX^T)}{\partial X}=X(A+A^T) ∂Xtr(∂XAXT)=X(A+AT) ↩︎