Leetcode.1735 生成乘积数组的方案数

题目链接

Leetcode.1735 生成乘积数组的方案数 rating : 2500

题目描述

给你一个二维整数数组 q u e r i e s queries queries ，其中 q u e r i e s [ i ] = [ n i , k i ] queries[i] = [n_i, k_i] queries[i]=[ni,ki] 。第 i i i 个查询 q u e r i e s [ i ] queries[i] queries[i] 要求构造长度为 n i n_i ni 、每个元素都是正整数的数组，且满足所有元素的乘积为 k i k_i ki ，请你找出有多少种可行的方案。由于答案可能会很大，方案数需要对 1 0 9 + 7 10^9 + 7 109+7 取余。

请你返回一个整数数组 a n s w e r answer answer，满足 a n s w e r . l e n g t h = = q u e r i e s . l e n g t h answer.length == queries.length answer.length==queries.length ，其中 a n s w e r [ i ] answer[i] answer[i] 是第 i i i 个查询的结果。

示例 1：

输入：queries = [[2,6],[5,1],[73,660]]
输出：[4,1,50734910]
解释：每个查询之间彼此独立。
[2,6]：总共有 4 种方案得到长度为 2 且乘积为 6 的数组：[1,6]，[2,3]，[3,2]，[6,1]。
[5,1]：总共有 1 种方案得到长度为 5 且乘积为 1 的数组：[1,1,1,1,1]。
[73,660]：总共有 1050734917 种方案得到长度为 73 且乘积为 660 的数组。1050734917 对 109 + 7 取余得到 50734910 。

示例 2：

输入：queries = [[1,1],[2,2],[3,3],[4,4],[5,5]]
输出：[1,2,3,10,5]

提示：

1 ≤ q u e r i e s . l e n g t h ≤ 1 0 4 1 \leq queries.length \leq 10^4 1≤queries.length≤104
1 ≤ n i , k i ≤ 1 0 4 1 \leq n_i, k_i \leq 10^4 1≤ni,ki≤104

解法：组合数学 + 质因数分解

对于 [ n i , k i ] [n_i, k_i] [ni,ki] 就等价于 有 n i n_i ni 个相同的箱子，要把 k i k_i ki 的所有质因子放入到这 n i n_i ni 箱子中，有的箱子可以为空。

例如 [ 2 , 6 ] [2, 6] [2,6]，就是有 2 2 2 个箱子 [ ] [ ] [\ ] [\ ] [ ][ ]， n = 2 × 3 n = 2 \times 3 n=2×3。一共有 4 4 4 种放法：

[ 2 ∗ 3 ] [ ] [2 * 3 ] [\ ] [2∗3][ ]
[ ] [ 2 ∗ 3 ] [\ ] [2 * 3] [ ][2∗3]
[ 2 ] [ 3 ] [2] [3] [2][3]
[ 3 ] [ 2 ] [3] [2] [3][2]

我们可以发现，对于不同的质因子都可以单独计算。假设这里把质因子 2 2 2 看作是小球 A A A，把质因子 3 3 3 看作是小球 B B B。

把小球 A A A 放到两个箱子中，一共有两种放法： [ A ] [ ] , [ ] [ A ] [A] [\ ], [\ ] [A] [A][ ],[ ][A]
把小球 B B B 放到两个箱子中，一共有两种放法： [ B ] [ ] , [ ] [ B ] [B] [\ ], [\ ] [B] [B][ ],[ ][B]

所以一共有 2 × 2 = 4 2 \times 2 = 4 2×2=4 种放法。

假设一共有 m m m 个箱子， n n n 个球，把 n n n 个球放进 m m m 个箱子，并且允许出现空箱子的放法有多少种。

等价于一共有 n + m n + m n+m 个球，要把这 n + m n + m n+m 个球分割成 m m m 部分，也就是 C ( n + m − 1 , m − 1 ) = C ( n + m − 1 , n ) C(n + m - 1, m - 1) = C(n + m - 1, n) C(n+m−1,m−1)=C(n+m−1,n)。

例如：假设有 3 3 3 个小球，要放到 4 4 4 个盒子中。

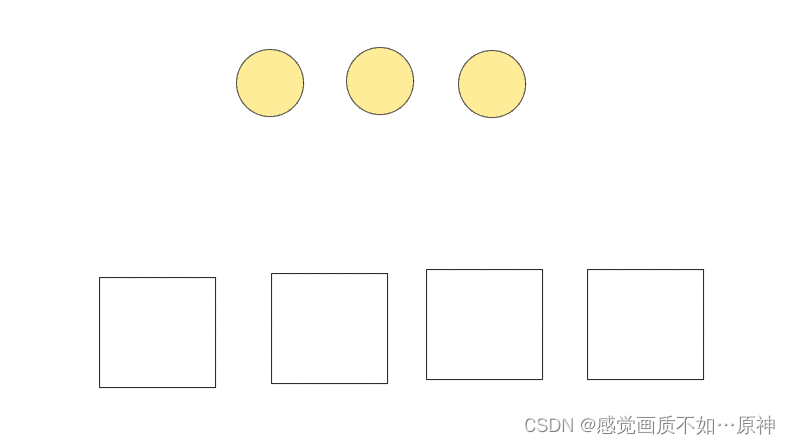
等价于有 3 + 4 3 + 4 3+4 个小球，再把小球分为 4 4 4 个部分的方案数量。

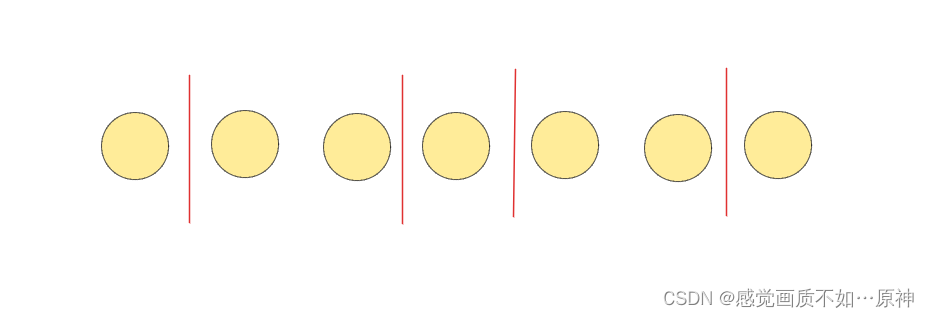
3 + 4 3 +4 3+4 个小球，一共有 3 + 4 − 1 = 6 3 + 4 - 1 = 6 3+4−1=6 个位置，要把这 7 7 7 个小球分为 4 4 4 个部分，直接从 6 6 6 个隔板中选 4 4 4 个插入，即 C ( 6 , 4 ) C(6, 4) C(6,4)；

推广到 n n n 个小球， m m m 个箱子就是 C ( n + m − 1 , m − 1 ) = C ( n + m − 1 , n ) C(n + m - 1, m - 1) = C(n + m - 1, n) C(n+m−1,m−1)=C(n+m−1,n)。

那么我们就可以处理出 k i k_i ki 的所有质因数，也就是求出所有小球，最后计算方案即可。

时间复杂度： ( ( N + l o g K ) l o g K ) ((N + logK) logK) ((N+logK)logK)

C++代码：

cpp 复制代码

using LL = long long;
const int MOD = 1e9 + 7;
const int N = 1e4 + 15;
LL c[N][15];

auto _ = []()
{
    c[0][0] = 1;
    for(int i = 1;i < N;i++)
    {
        c[i][0] = 1;
        for(int j = 1;j < 15;j++) c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % MOD;
    }
    return 0;
}();

class Solution {
public:
    vector<int> waysToFillArray(vector<vector<int>>& queries) {
        vector<int> ans;

        for(auto q:queries)
        {
            int n = q[0], k = q[1];
            LL res = 1;
            auto x = k;

            for(int i = 2;i <= x / i;i++)
            {
                if(x % i == 0)
                {
                    int cnt = 0;
                    while(x % i == 0)
                    {
                        x /= i;
                        cnt++;
                    }

                    res = res * c[cnt + n - 1][cnt] % MOD;
                }
            }

            if(x > 1) res = res * n % MOD;
            ans.push_back(res);
        }

        return ans;
    }
};