这里写目录标题
本专栏旨在记录本人解决问题的思考方法,及实现过程。有更好方法或对程序执行有疑问的伙伴,可在评论区留言,共同讨论。
这里写目录标题
一级目录
二级目录
三级目录
题目要求
- 定义: 谢尔宾斯基三角形最早由波兰数学家谢尔宾斯基在1915年提出。它的构造方法是:以一个正三角形为初始图形,每次将正三角形分割成4个边长为原来一半的小三角形,并去掉其中间的小三角形,重复这一过程,直到不能再分割为止。
- 要求: 用最简单的代码,绘制出谢尔宾斯基三角形。
最终结果
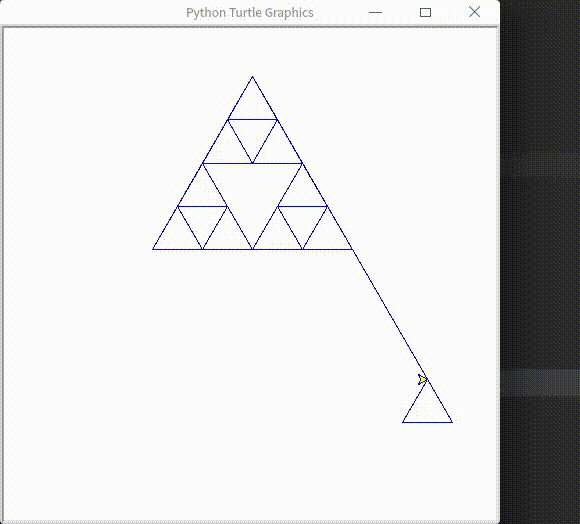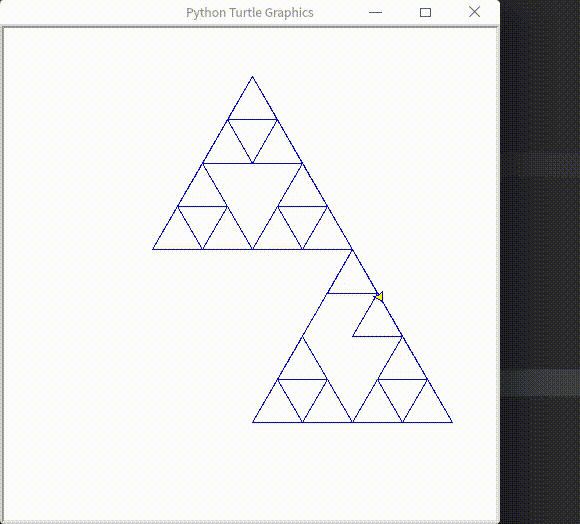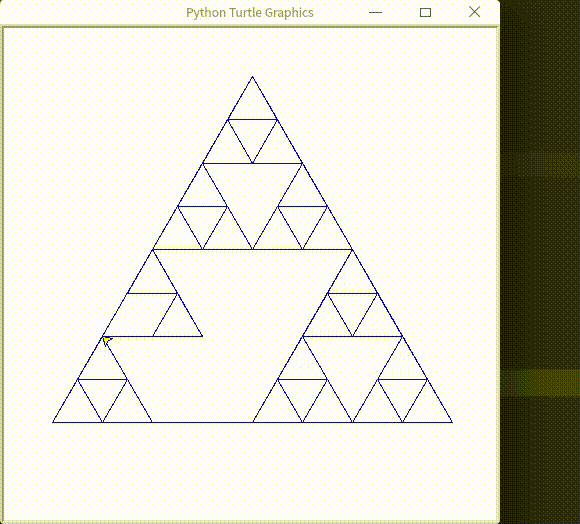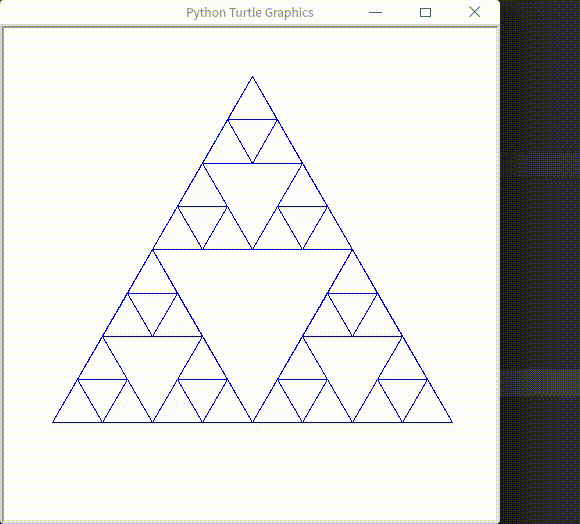

解决流程
绘制中发现,如果完全按照定义,通过每次截取的方式(每次在三角形中截取一个三角形),则需用到大量的计算,如何确定每一次画笔的位置也是一个难题。
本人在绘制中,通过按边绘制,如果非最后一层,则取半绘制三角形,这样减少了计算量,并且只用 6 段代码就实现了谢尔斯基三角形的绘制。
程序实现
python
import turtle
turtle.setup(500,500) # 窗口大小
turtle.screensize(400, 400) # 画布大小
#turtle.tracer(False) # 省略绘制过程
t = turtle.Turtle()
t.penup()
t.goto(0, 200)
t.pendown()
t.color('blue', 'yellow')
t.left(60)
# 定义基本参数
bc = 400 # 边长
# 绘制函数
def huasj(n, jbc):
if n != 0:
for _ in range(3):
huasj(n - 1, jbc / 2)
t.right(120)
t.forward(jbc)
#绘制连长为 400 的 5 层三角形
huasj(5, bc)
t.hideturtle()
turtle.update() # 更新画布
turtle.done()** 递归绘制函数:**
python
def huasj(n, jbc):
if n != 0:
for _ in range(3):
huasj(n - 1, jbc / 2)
t.right(120)
t.forward(jbc)** 递归函数说明:** 1.递归结束条件,层数为0时不执行;2.递归执行过程,如果 n > 1 ,则执行 n - 1。
运行示例
下图为连长为400, 层数为7的 谢尔宾斯基三角形 示例:

小结
该方法,仍然受到递归限制,层数不能增大,同时在 liunx 中运行画三角形时,不能进行色彩填充。