题干:
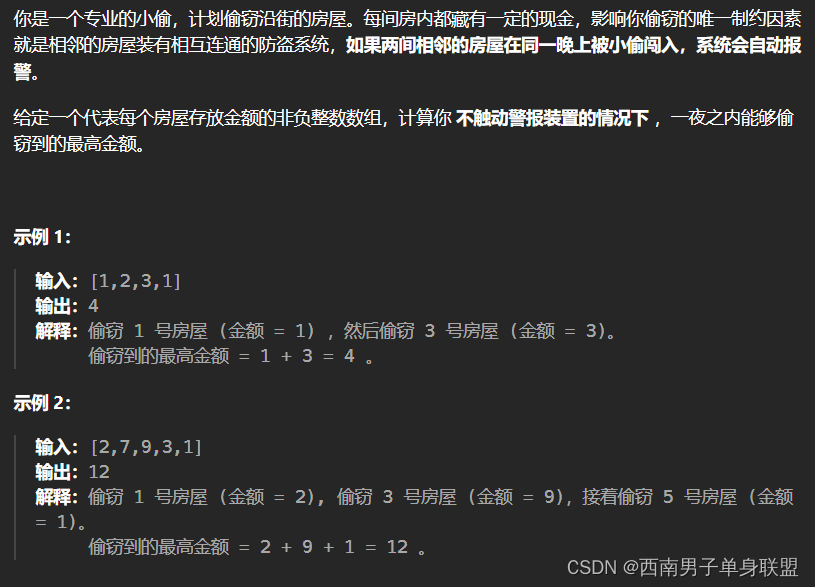
代码:
cpp
class Solution {
public:
int rob(vector<int>& nums) {
if(nums.size() == 0)return 0;
if(nums.size() == 1)return nums[0];
vector<int>dp(nums.size(), 0);
dp[0] = nums[0];
dp[1] = max(nums[0], nums[1]);
for(int i = 2; i < nums.size(); i++){
dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
}
return dp[nums.size() - 1];
}
};思路:当前房屋偷与不偷取决于 前一个房屋和前两个房屋是否被偷了。发现当前状态和前面状态会有一种依赖关系,那么这种依赖关系都是动规的递推公式。
1.确定dp数组(dp table)以及下标的含义
dp[i]:考虑下标i(包括i)以内的房屋,最多可以偷窃的金额为dp[i]。
2.确定递推公式
决定dp[i]的因素就是第i房间偷还是不偷。
如果偷第i房间,那么dp[i] = dp[i - 2] + nums[i] ,即:第i-1房一定是不考虑的,找出 下标i-2(包括i-2)以内的房屋,最多可以偷窃的金额为dp[i-2] 加上第i房间偷到的钱。
如果不偷第i房间,那么dp[i] = dp[i - 1],即考 虑i-1房,(注意这里是考虑,并不是一定要偷i-1房)
然后dp[i]取最大值,即dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
3.dp数组如何初始化
从递推公式dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);可以看出,递推公式的基础就是dp[0] 和 dp[1]
从dp[i]的定义上来讲,dp[0] 一定是 nums[0],dp[1]就是nums[0]和nums[1]的最大值即:dp[1] = max(nums[0], nums[1]);
4.遍历顺序:有i - 2 >= 0得到从2开始。