1、基于归一化感知器的输入向量分类的原理及流程
归一化感知器是一种分类算法,其原理基于感知器算法,但是在输入向量上进行了归一化处理,以提高算法的性能和稳定性。
流程如下:
- **输入向量归一化:**对每个输入向量进行归一化处理,将其值缩放到一定的范围内,通常是将每个特征值除以其范数(模长)。
- **初始化参数:**初始化权重向量和偏置项。
- **计算预测值:**根据当前的权重向量和偏置项,计算输入向量的预测值。
- **判断分类结果:**根据预测值判断输入向量的分类结果。
- **更新参数:**根据分类结果和真实标签之间的差异,更新权重向量和偏置项。
- **重复步骤3至步骤5:**迭代计算,直至收敛或达到设定的迭代次数。
通过归一化感知器,可以更加准确地区分不同的类别,在处理高维度数据时也可以有效防止输入向量之间的差异对分类结果的影响。
2、归一化感知器的输入向量分类说明
解决问题
2 输入硬限制神经元被训练为将 5 个输入向量分类为两个类别。
说明
一个输入向量比其他输入向量大得多,使用 LEARNPN 进行训练还是很快的。
3、输入数据
说明
X 中的五个列向量中的每一个都定义了一个二元素输入向量,行向量 T 定义了向量的目标类别。
4 个输入向量的幅值远远小于绘图左上角的第五个向量。
感知器必须将 X 中的 5 个输入向量正确分类为由 T 定义的两个类别。
代码
Matlab
X = [ -0.5 -0.5 +0.3 -0.1 -40; ...
-0.5 +0.5 -0.5 +1.0 50];
T = [1 1 0 0 1];
figure(1)
plotpv(X,T);视图效果
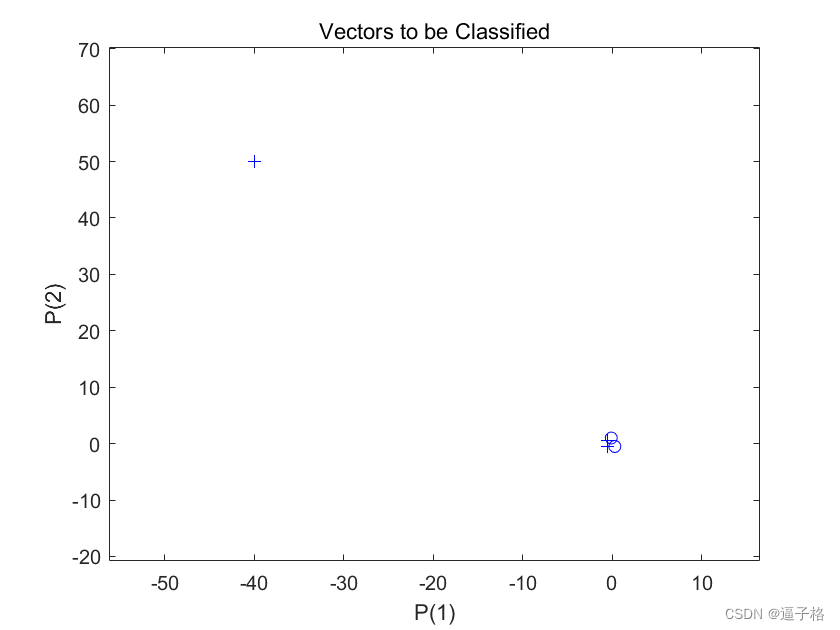
3、创建网络
说明
PERCEPTRON 用 LEARPN 规则创建一个新网络,相对于 LEARNP(默认值),该网络对输入向量大小的巨大变化不太敏感。
用输入数据和目标数据对该网络进行配置,得到其权重和偏置的初始值。
代码
Matlab
net = perceptron('hardlim','learnpn');
net = configure(net,X,T);4、将神经元的最初分类尝试添加到绘图中
说明
初始权重设置为零,因此任何输入都会生成相同的输出,而且分类线甚至不会出现在图上。
代码
Matlab
hold on
linehandle = plotpc(net.IW{1},net.b{1});视图效果

5、 返回新网络对象(它作为更好的分类器执行)、网络输出和误差
说明
ADAPT 返回一个新网络对象(它作为更好的分类器执行)、网络输出和误差。此循环允许网络自适应,绘制分类线,并继续进行直到误差为零。
用 LEARNP 进行训练只需要 3 轮,而用 LEARNPN 求解同样的问题需要 32 轮。因此,当输入向量大小有巨大变化时,LEARNPN 的表现优于 LEARNP。
代码
Matlab
E = 1;
while (sse(E))
[net,Y,E] = adapt(net,X,T);
linehandle = plotpc(net.IW{1},net.b{1},linehandle);
drawnow;
end视图效果
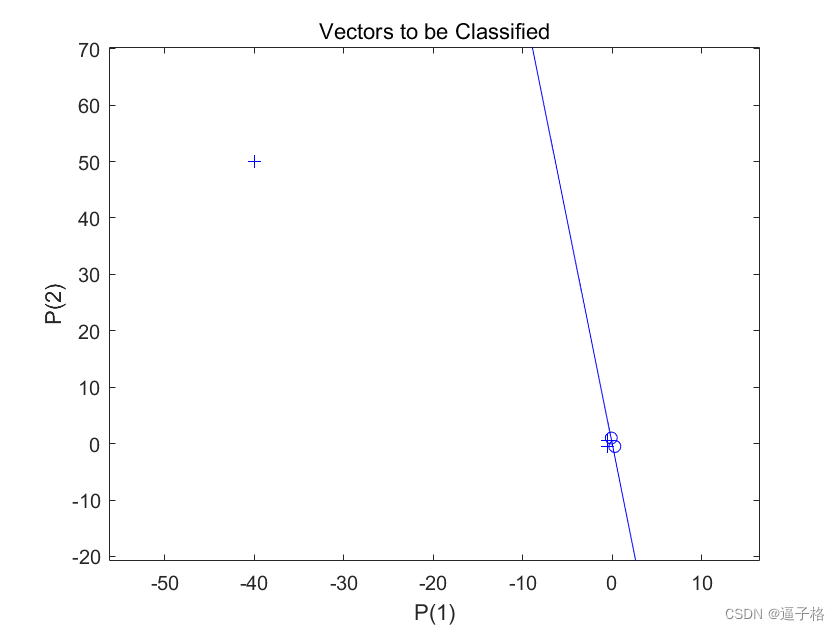
6、对输入向量 [0.7; 1.2] 进行分类
说明
此新点及原始训练集的绘图显示了网络的性能。为了将其与训练集区分开来,将其显示为红色。
代码
Matlab
x = [0.7; 1.2];
y = net(x);
% figure(2)
plotpv(x,y);
circle = findobj(gca,'type','line');
circle.Color = 'red';视图效果

7、将训练集和分类线添加到绘图中
代码
Matlab
hold on;
plotpv(X,T);
plotpc(net.IW{1},net.b{1});
hold off;视图效果
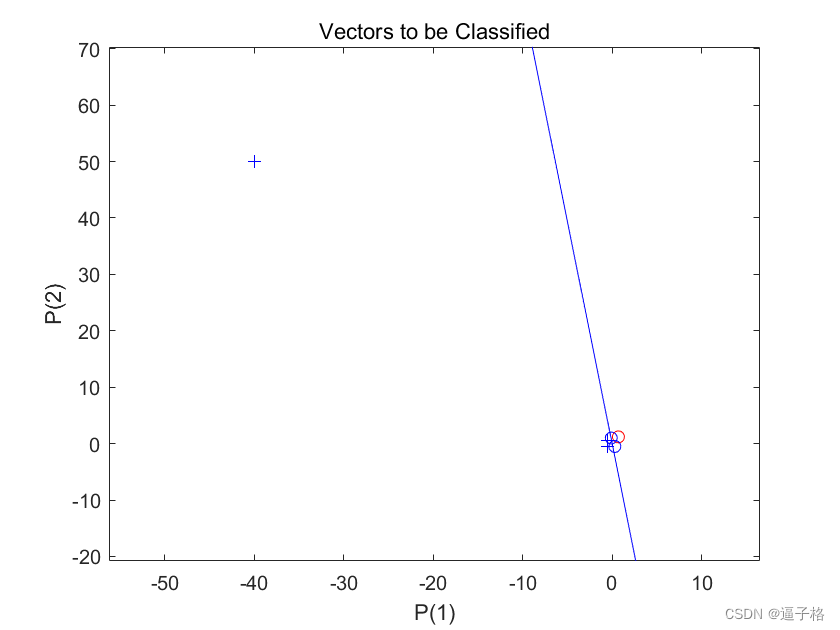
8、局部放大
说明
感知器正确地将我们的新点(红色)分类为类别"零"(用圆圈表示)而不是"一"(用加号表示)。尽管存在离群值,感知器仍能在短得多的时间内正确学习
代码
Matlab
axis([-2 2 -2 2]);视图效果
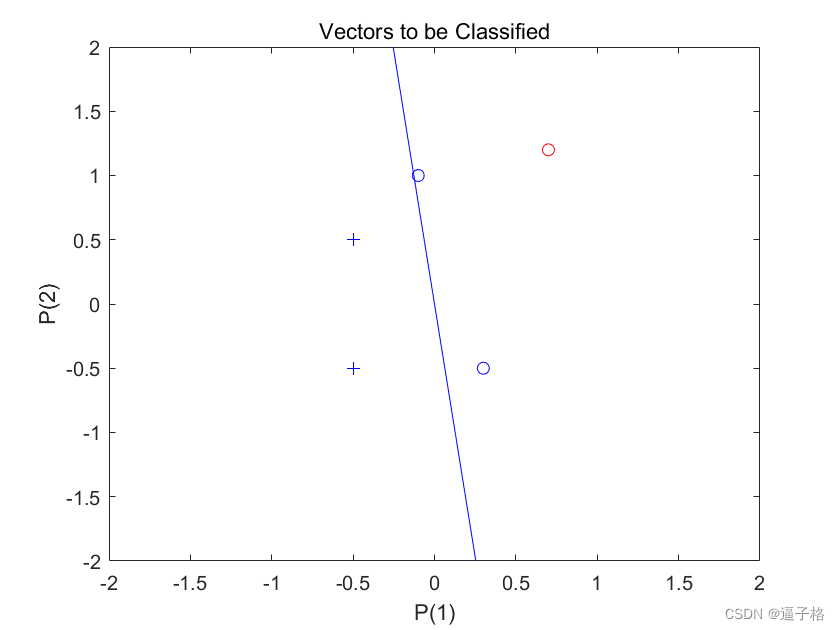
9、总结
在MATLAB中实现基于归一化感知器的输入向量分类可以按照以下步骤进行:
-
数据准备:准备包含特征值和标签的训练数据集。确保特征值已经进行了归一化处理。
-
参数初始化:初始化权重向量和偏置项,可以随机初始化或者设置为零向量。
-
训练模型:利用训练数据集训练归一化感知器模型。通过迭代计算,更新权重向量和偏置项,直至模型收敛或达到设定的迭代次数。
-
预测分类:利用训练好的感知器模型对测试数据集进行分类预测,计算准确率或者其他评估指标。
以下是一个简单的示例代码,演示如何在MATLAB中实现归一化感知器的输入向量分类:
Matlab
% 准备训练数据集
X_train = ...; % 特征值矩阵,已进行归一化处理
Y_train = ...; % 标签向量
% 初始化参数
W = zeros(size(X_train, 2), 1); % 权重向量
b = 0; % 偏置项
% 训练模型
max_iter = 1000; % 最大迭代次数
alpha = 0.1; % 学习率
for iter = 1:max_iter
for i = 1:size(X_train, 1)
y_pred = sign(dot(W, X_train(i, :)) + b);
if y_pred ~= Y_train(i) W = W + alpha * Y_train(i) * X_train(i, :)';
b = b + alpha * Y_train(i);
end
end
end
% 预测分类
X_test = ...; % 测试数据集特征值矩阵
Y_test = ...; % 测试数据集标签向量
correct = 0;
for i = 1:size(X_test, 1)
y_pred = sign(dot(W, X_test(i, :)) + b);
if y_pred == Y_test(i) correct = correct + 1;
end
end
accuracy = correct / size(X_test, 1);
disp(['Accuracy: ', num2str(accuracy)]);以上代码演示了如何使用MATLAB实现基于归一化感知器的输入向量分类。在实际应用中,可以根据具体的数据集和问题进行参数调整和优化,以获得更好的分类结果。
10、源代码
代码
Matlab
%% 归一化感知器规则
%说明:2 输入硬限制神经元被训练为将 5 个输入向量分类为两个类别。
%一个输入向量比其他输入向量大得多,使用 LEARNPN 进行训练还是很快的。
%% 输入数据
%说明:X 中的五个列向量中的每一个都定义了一个二元素输入向量,行向量 T 定义了向量的目标类别。
%4 个输入向量的幅值远远小于绘图左上角的第五个向量。
%感知器必须将 X 中的 5 个输入向量正确分类为由 T 定义的两个类别。
X = [ -0.5 -0.5 +0.3 -0.1 -40; ...
-0.5 +0.5 -0.5 +1.0 50];
T = [1 1 0 0 1];
figure(1)
plotpv(X,T);
%% 创建网络
%PERCEPTRON 用 LEARPN 规则创建一个新网络,相对于 LEARNP(默认值),该网络对输入向量大小的巨大变化不太敏感。
%用输入数据和目标数据对该网络进行配置,得到其权重和偏置的初始值。
net = perceptron('hardlim','learnpn');
net = configure(net,X,T);
%% 将神经元的最初分类尝试添加到绘图中
%初始权重设置为零,因此任何输入都会生成相同的输出,而且分类线甚至不会出现在图上。
hold on
linehandle = plotpc(net.IW{1},net.b{1});
%% 返回新网络对象(它作为更好的分类器执行)、网络输出和误差
%ADAPT 返回一个新网络对象(它作为更好的分类器执行)、网络输出和误差。此循环允许网络自适应,绘制分类线,并继续进行直到误差为零
%用 LEARNP 进行训练只需要 3 轮,而用 LEARNPN 求解同样的问题需要 32 轮。因此,当输入向量大小有巨大变化时,LEARNPN 的表现优于 LEARNP。
E = 1;
while (sse(E))
[net,Y,E] = adapt(net,X,T);
linehandle = plotpc(net.IW{1},net.b{1},linehandle);
drawnow;
end
%% 对输入向量 [0.7; 1.2] 进行分类。
%此新点及原始训练集的绘图显示了网络的性能。为了将其与训练集区分开来,将其显示为红色。
x = [0.7; 1.2];
y = net(x);
% figure(2)
plotpv(x,y);
circle = findobj(gca,'type','line');
circle.Color = 'red';
%% 将训练集和分类线添加到绘图中
hold on;
plotpv(X,T);
plotpc(net.IW{1},net.b{1});
hold off;
%% 局部方法
%感知器正确地将我们的新点(红色)分类为类别"零"(用圆圈表示)而不是"一"(用加号表示)。尽管存在离群值,感知器仍能在短得多的时间内正确学习
axis([-2 2 -2 2]);