目录
- [585. 2016年的投资](#585. 2016年的投资)
- [438. 找到字符串中所有字母异位词](#438. 找到字符串中所有字母异位词)
- [98. 验证二叉搜索树](#98. 验证二叉搜索树)
585. 2016年的投资
题目链接
表
- 表
Insurance的字段为pid、tiv_2015、tiv_2016、lat和lon。
要求
编写解决方案报告 2016 年 (tiv_2016) 所有满足下述条件的投保人的投保金额之和:
- 他在 2015 年的投保额 (
tiv_2015) 至少跟一个其他投保人在 2015 年的投保额相同。 - 他所在的城市必须与其他投保人都不同(也就是说 (
lat, lon) 不能跟其他任何一个投保人完全相同)。
tiv_2016 四舍五入的 两位小数 。
知识点
count():统计个数的函数。round():四舍五入的函数。group by:根据某些字段分组。having:对分组后的结果进行限制。in:将字段的值限制到某个集合内。
思路
从要求中可以看出,本题对原表Insurance的数据有两个限制。
第一个限制很好解决,只需要让2015年的投保额tiv_2015在表中出现一次以上即可,这就要统计每个tiv_2015出现的次数,然后筛选出tiv_2015出现次数超过1次的值,接着将表Insurance的tiv_2015限制到(in)出现次数超过1次的tiv_2015中。
第二个限制需要思考一下,经度lon的范围为[-180, 180],纬度lat的范围为[-90, 90],所以可以给纬度lat乘1000,然后与经度lon相加,这样就会得到一个唯一的经纬度组合lat * 1000 + lon,每条数据都有这个唯一的经纬度组合。接着在表中统计只出现过一次的经纬度组合,将表Insurance的经纬度组合限制到(in)这些只出现过一次的经纬度组合中。
注意:官方题解中对第二个限制使用了concat()拼接函数,将lat, lon拼接起来,这种方式就不需要计算了。
代码
sql
select
round(sum(tiv_2016), 2) tiv_2016
from
Insurance
where
tiv_2015 in (
select
tiv_2015
from
Insurance
group by
tiv_2015
having
count(*) > 1
)
and
lat * 1000 + lon in (
select
lat * 1000 + lon
from
Insurance
group by
lat, lon
having
count(*) = 1
)438. 找到字符串中所有字母异位词
题目链接
标签
哈希表 字符串 滑动窗口
思路
要写出本题的答案,得先了解异位词 的概念:异位词 指由相同字母重排列形成的字符串(包括相同的字符串)。也就是说异位词 不关心字符的顺序,只关心字符出现的次数,所以顺理成章地使用一个int[]统计字符出现的次数,由于s, p只含小写字符,所以只需要使用一个长度为26的int[]。
先使用int[] target统计目标字符串的字符情况,然后再使用int[] window统计 以原字符串第一个字符s.charAt(0)作为起始字符的窗口 的字符情况,统计完毕后将两个数组进行比较,如果一致,则说明 以原字符串第一个字符s.charAt(0)作为起始字符的窗口 是 目标字符串 的异位词,将窗口第一个字符的索引0加入结果链表。
之后滑动窗口,直到窗口滑动到字符串末尾。每次滑动窗口的之前,先去除窗口的第一个字符,然后再给窗口新增一个字符,接着判断这个窗口的字符情况是否与目标字符串的字符情况一致,如果一致,则记录更新后的窗口(即去除和增加字符后的窗口)的第一个字符的索引。
代码
java
class Solution {
public List<Integer> findAnagrams(String s, String p) {
char[] sC = s.toCharArray();
char[] pC = p.toCharArray();
int n = sC.length, m = pC.length;
// 如果待匹配字符串的长度比目标字符串的长度小,则返回空集合
if (n < m) {
return new ArrayList<>();
}
// 先统计 以sC[0]开头的窗口 的字符 和 目标字符串 的字符
List<Integer> res = new ArrayList<>();
int[] window = new int[26]; // 用来统计窗口内的字符情况
int[] target = new int[26]; // 用来统计目标字符串的字符情况
for (int i = 0; i < m; i++) {
target[pC[i] - 'a']++;
window[sC[i] - 'a']++;
}
// 如果 窗口 和 目标字符串 的字符情况一样,则将0存入结果链表
if (Arrays.equals(target, window)) {
res.add(0);
}
// 滑动窗口,对每个子串进行判断
for (int i = 0; i < n - m; i++) {
window[sC[i] - 'a']--; // 移除窗口的第一个字符
window[sC[i + m] - 'a']++; // 加入新字符
// 如果 窗口 和 目标字符串 的字符情况一样,则将i + 1存入结果链表
// 为什么是i + 1而不是i?因为此时已将索引为i的字符从窗口中移除了,窗口的第一个字符的索引为i + 1
if (Arrays.equals(target, window)) {
res.add(i + 1);
}
}
return res;
}
}98. 验证二叉搜索树
题目链接
标签
树 深度优先搜索 二叉搜索树 二叉树
合法区间
思路
判断一个二叉树是否是有效的二叉搜索树,就是判断它的每个节点是否满足左子节点的值小于父节点,右子节点的值大于父节点 。可以使用两个值min, max记录一个节点的值的合法区间,左子节点的合法区间就是(父节点的min, 父节点的值),右子节点的合法区间就是(父节点的值, 父节点的max),注意:这里的区间都是开区间。初始的min为Long.MIN_VALUE、max为Long.MAX_VALUE,这表示根节点的值可以为任意值,不需要限制。
由于本题的测试样例比较特殊,所以min, max的类型不能是int,而是long。
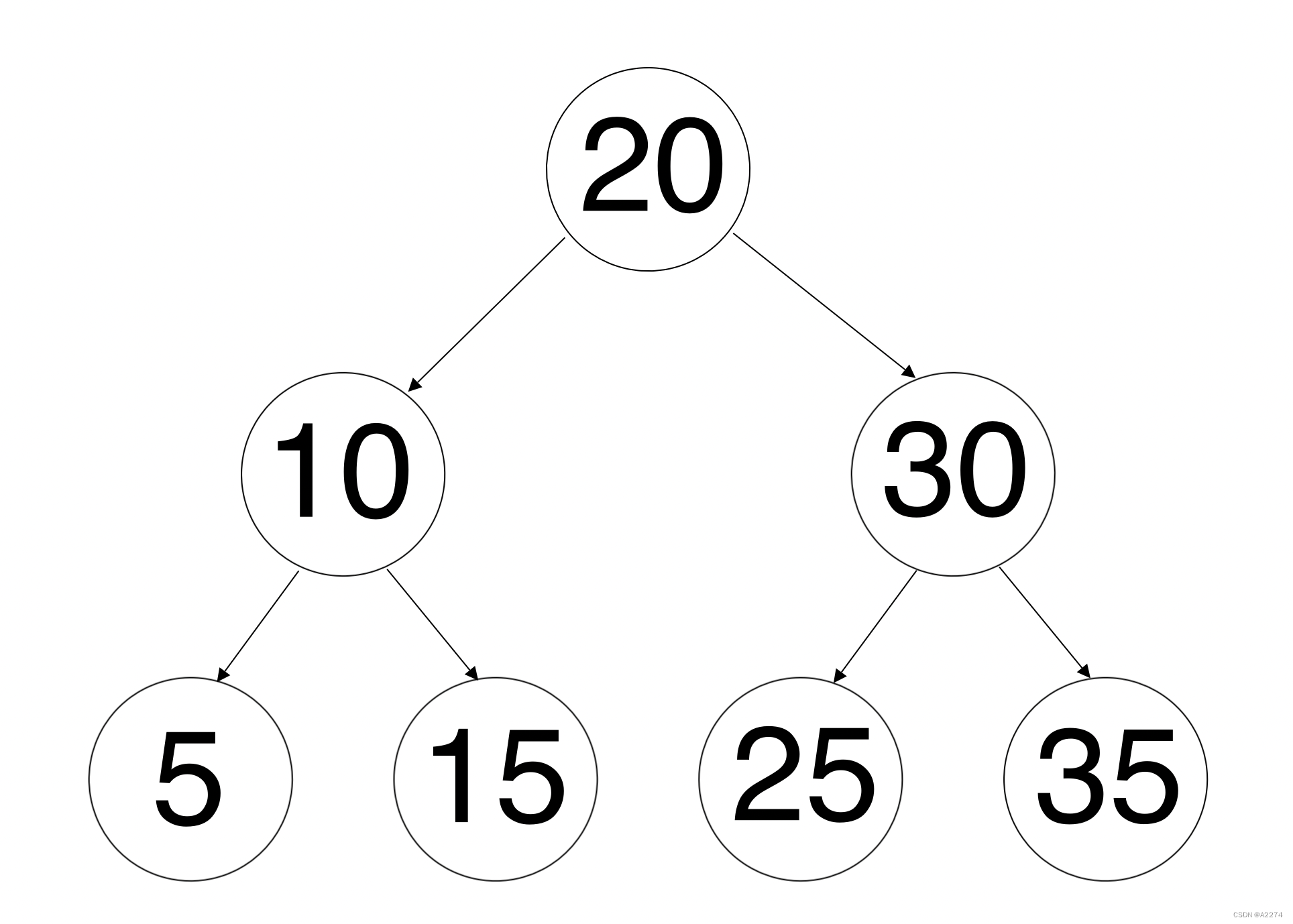
例如上面这颗二叉树:
节点20的限制为(Long.MIN_VALUE, Long.MAX_VALUE)
节点10的限制为(Long.MIN_VALUE, 20)
节点5的限制为(Long.MIN_VALUE, 10)
节点15的限制为(10, 20)
节点30的限制为(20, Long.MAX_VALUE)
节点25的限制为(20, 30)
节点35的限制为(30, Long.MAX_VALUE)
代码
java
class Solution {
public boolean isValidBST(TreeNode root) {
return judge(root, Long.MIN_VALUE, Long.MAX_VALUE);
}
// 判断当前节点的值是否在限制的区间(min, max)内
private boolean judge(TreeNode curr, long min, long max) {
if (curr == null) { // 如果本节点为null
return true; // 则是合法的二叉搜索树
}
if (curr.val <= min || curr.val >= max) { // 如果当前节点的值不在区间内
return false; // 则不是合法的二叉搜索树
}
return judge(curr.left, min, curr.val) // 判断左子树是否是合法
&& judge(curr.right, curr.val, max); // 判断右子树是否合法
}
}中序遍历
思路
二叉搜索 树的中序遍历 是有特殊意义的,结果恰好为一个升序的数组。例如上面那张图中序遍历的结果为[5, 10, 15, 20, 25, 30, 35]。
对中序遍历不熟悉的可以看这篇文章:94. 二叉树的中序遍历。
故可以使用中序遍历求出当前值的前一个值,如果当前值不大于前一个值,那么这棵树就不是一个有效的二叉搜索树。
所以本解法的重点就是找前一个值,可以使用递归,先遍历左子树(遍历左子树的目的就是为了找前一个节点的值),然后再将本节点与前一个节点进行比较,接着更新前一个节点的值,再比较右子树,最后返回比较的结果。
代码
java
class Solution {
private long prevVal = Long.MIN_VALUE; // 存储前一个节点的值
public boolean isValidBST(TreeNode curr) {
if (curr == null) { // 如果本节点为null
return true; // 则是合法的二叉搜索树
}
boolean left = isValidBST(curr.left); // 判断左子树是否是合法(遍历左子树,找前一个节点的值)
if (!(curr.val > prevVal)) { // 如果当前节点的值 不大于 前一个节点的值
return false; // 则不是合法的二叉搜索树
}
prevVal = curr.val; // 更新前一个节点的值,为右子树的比较做准备
boolean right = isValidBST(curr.right); // 判断右子树是否合法(遍历右子树)
return left && right; // 返回判断结果
}
}