数值稳定性
其中h是一个向量,向量关于向量的倒数是一个矩阵,因此求梯度是求矩阵乘法

矩阵乘法带来了 梯度爆炸,梯度消失



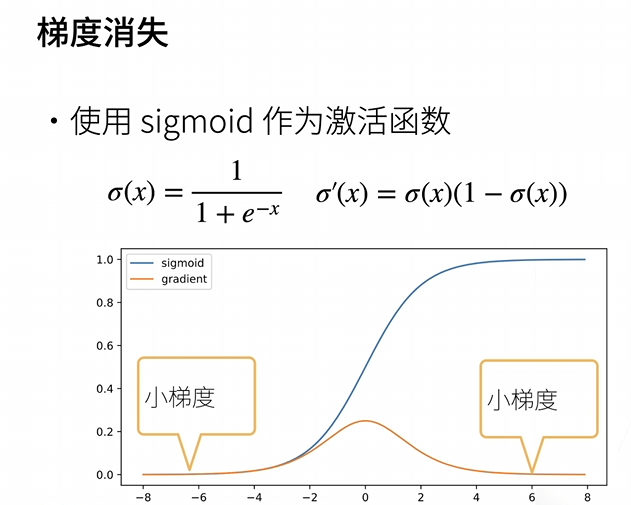

模型初始化和激活函数

归一化:不管梯度多大,我都把梯度拉回来,否的出现梯度爆炸和梯度消失问题。

不管做多深,都能在一个合理范围内
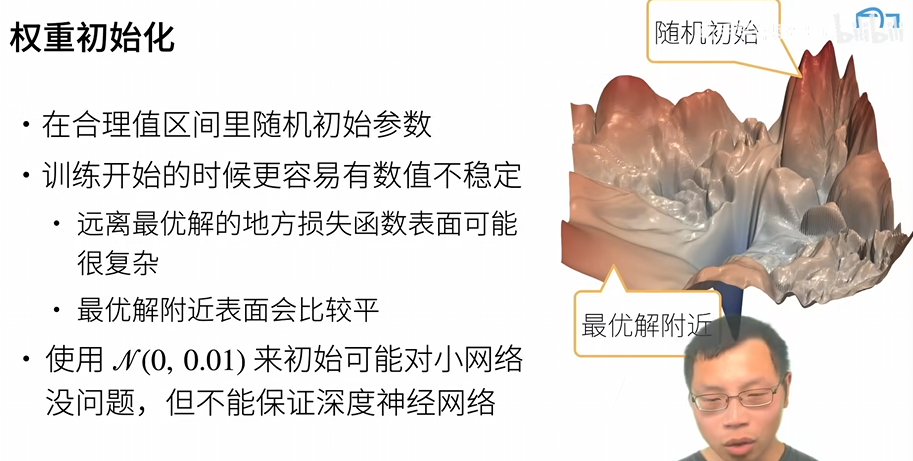
假设权重是独立同分布,定义均值和方差,t是层数

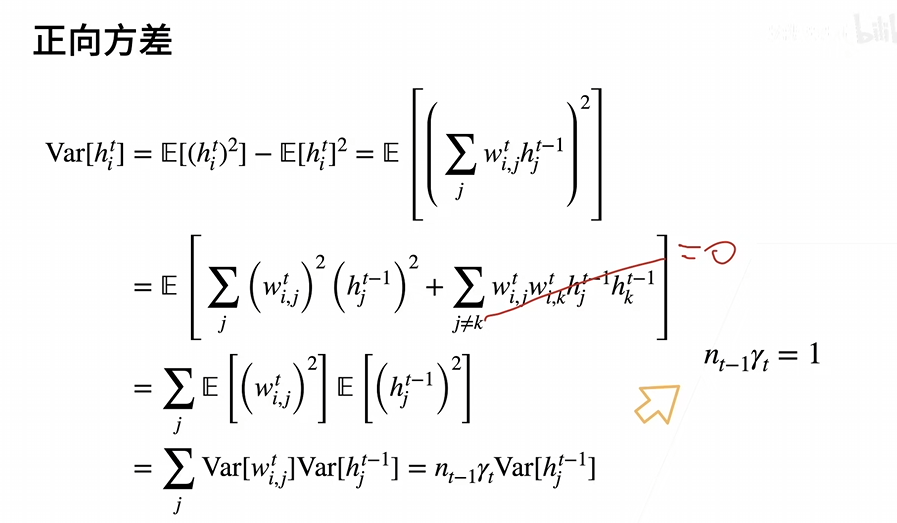
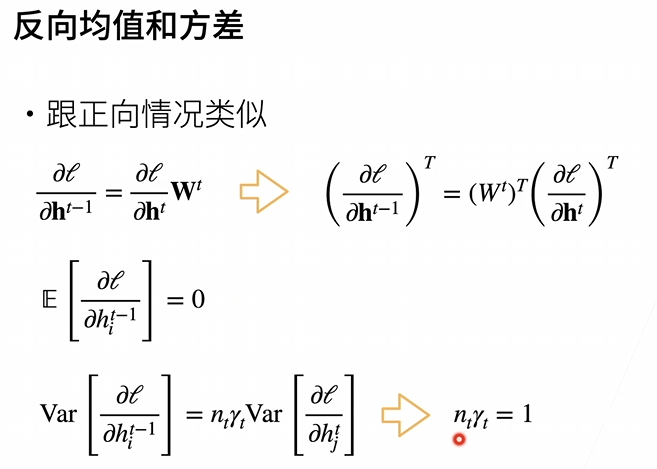
nt-1是t层输入的维度,nt是输出的维度,除非输入等于输入,除非无法相等
γt是第t层权重的方差
不能满足同时,取个折中,给定当前层和输出层权重大小,就能确定方差大小。
采用正态分布,当前值是0,方差不是固定的0.01了,是根据输入输出决定的。

如果想使得前项输出的均值和方差都是0,固定,那么β=0,α=1.

意味着什么?意味着激活函数fx必须=x,其中tanh和relu满足在0点附近,sigmoid改变后可以满足fx=x
补充:激活函数:如果不用激活函数,每一层输出都是上层输入的线性函数,如果使用,激活函数给神经元引入了非线性因素,使神经网络可以逼近任何非线性函数。
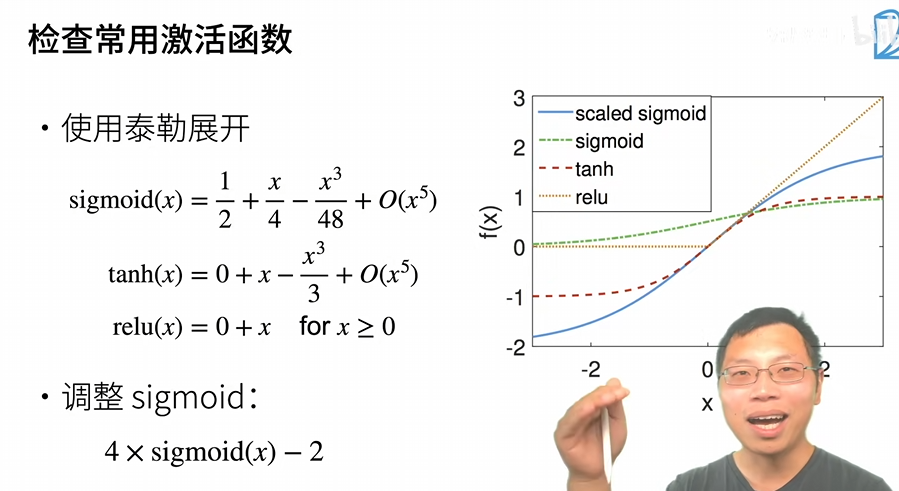
总结:可以通过合理的权重初始值和激活函数的选取提升数值的稳定性。
全连接层到卷积
一张图片中找信息,不能所有点都检查一遍。需要满足两个原则
平移不变性
局部性

现在x位置变换后,权重也得跟着变换,如何能让他不变。不管ij怎么变换,输出的地方挪到哪个位置,用的识别检测器v都应该不变的。
当把一个模型的取值范围做了限制,模型复杂度就降低了。也就不用存那么多元素了。

假设要算ij这个输出话,以i为中心,a可以任意变换的位置都要看一遍,但实际不应该看那么远的地方,只看附近就行。因此做出限制。


卷积层是特殊的全连接层
全连接层:卷积、池化、激活函数但是将原始数据映射到隐藏特征空间,全连接层是将学到的"分布式特征表示"映射到样本标记空间的作用。
卷积层
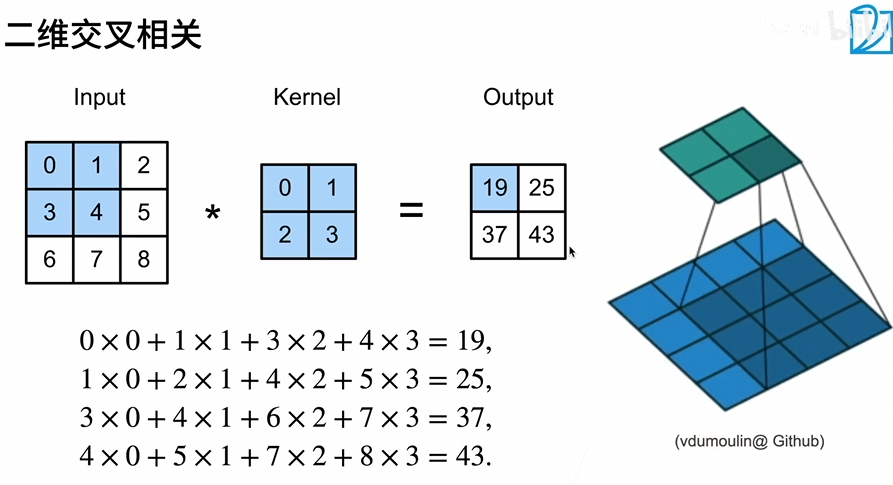
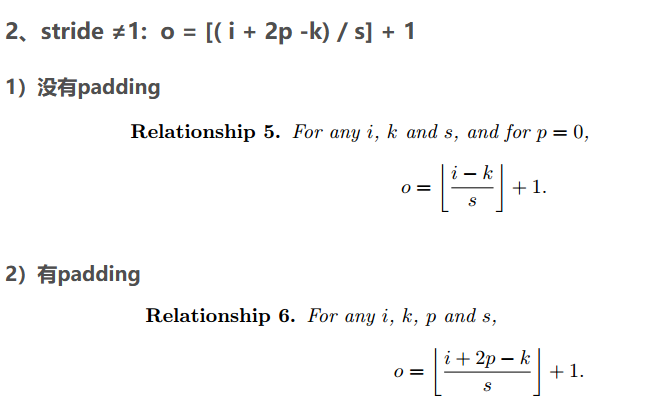
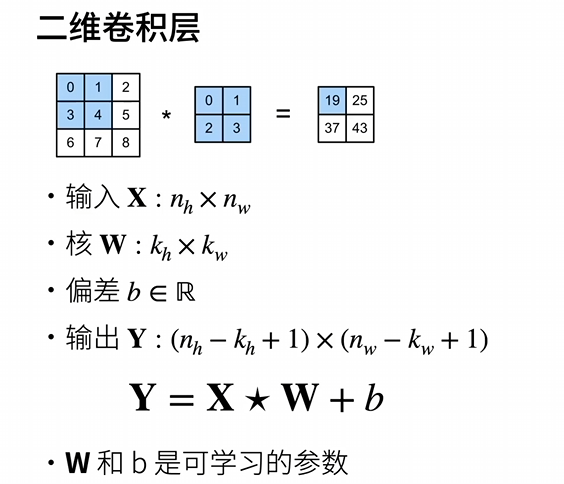
3、统一的公式:o = [( i + 2p - k) / s] + 1

说是卷积层,但是为了实现方便,将权重的负号改为了正,实际上是二维交叉相关

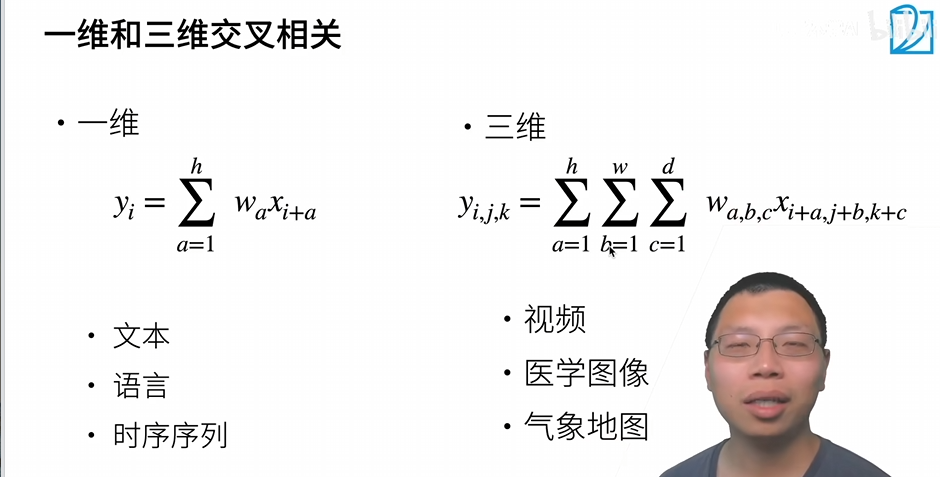
气象地图涉及到了时间
总结:
卷积层将输入和核矩阵进行交叉相关,加上偏移后得到输出
核矩阵和偏移时可学习的参数
核矩阵的大小是超参数(kernel的大小)
解决了问题:权重随着输入变得特别大,卷积不会有这个问题。