目录
[1. 特征向量和特征值代表什么含义？](#1. 特征向量和特征值代表什么含义？)
[2. 矩阵的秩是什么？满秩代表什么？不满秩呢？](#2. 矩阵的秩是什么？满秩代表什么？不满秩呢？)
[3. 奇异值分解是什么？](#3. 奇异值分解是什么？)
[4. 正定矩阵是什么？](#4. 正定矩阵是什么？)
[5. 相似矩阵是什么？](#5. 相似矩阵是什么？)
[6. 什么是线性相关？什么是线性无关？](#6. 什么是线性相关？什么是线性无关？)
[7. 正交矩阵是什么？](#7. 正交矩阵是什么？)
[10.两个矩阵A、B，什么情况下AB = BA](#10.两个矩阵A、B，什么情况下AB = BA)
1. 特征向量和特征值代表什么含义？
一句话解释矩阵可以看作是线性变换，那么特征值就是变换的幅度
特征向量就是变换的方向矩阵的特征向量是这样的向量：矩阵作用于该向量后，向量保持方向不变，进行某一比例的伸缩变换，而这个比例就是特征值。
因此，特征值与特征向量的关系就是，特征值与特征向量进行数乘操作后所得的向量，和矩阵对该向量进行变换后所得向量相同。
因此特征值的含义就是和矩阵具有同等变换效果的常数，而特征向量就是与矩阵作用之后能够保持方向不变的向量。
应用：特征值可以用于奇异值分解（SVD）、主成分分析（PCA）。
2. 矩阵的秩是什么？满秩代表什么？不满秩呢？
关于矩阵的秩有很多种理解方式，下面我谈一下在我的学习过程中对矩阵的秩的一些理解。
从极大线性无关组的角度出发
将矩阵按列分解为 n 个向量，组成一个向量组，则这个向量组的一个极大线性无关组中包含向量的个数 r 称为矩阵的行秩。同理可定义列秩，可证列秩 = 行秩。
从线性方程组的角度出发
我们可以把矩阵构造成一个线性方程组，但是里面可能会有一些重复冗余的方程，那我们把这些没用的方程去掉之后， 后剩下的方程个数就是秩。
线性方程组中真正是干货的方程个数，就是它对应矩阵的秩。
从向量空间的角度出发
秩是图像经过矩阵变换之后的空间维度。
比如原始图像是一个二维的，经过一个旋转矩阵进行变换之后，得到的图像是一个二维图形，所以旋转矩阵的秩就是2。而如果通过 [[1, -1], [1, -1]] 这个矩阵进行变换，得到的图像是一条一维直线，所以这个矩阵的秩就是1。
满秩和不满秩
从线性方程组的角度出发
满秩解出的是唯一解；不是满秩的话，解出的就是集合了。
从向量空间的角度出发
对于一个满秩变换来说，变换之后空间维度保持不变。
对于一个非满秩变换来说，它会把空间压缩到一个更低的维度上。
3. 奇异值分解是什么？
SVD 的公式
如果 M 是一个实数域上的 m × n 的矩阵，那么 M 就存在奇异值分解
其中 U 是 m 阶的正交矩阵，V 是 n 阶的正交矩阵，而 Σ 是一个 m × n 的对角矩阵，它对角线上的元素就是奇异值，并且是按照从大到小的顺序排列的。
SVD 的几何意义
在几何上看，SVD 分解就可以看作是将一个矩阵首先进行旋转，然后拉伸，然后再旋转的的操作。
SVD 的作用
在拿到了矩阵 M 的奇异值分解之后，我们可以把它展开成 \\sigma _i u_i v_i \^T 的形式。
其中奇异值 σ 的大小表示它所对应的矩阵在整体展开式当中的重要性，奇异值越大，就越重要。
在很多情况下，前 10%（甚至更少）的奇异值就占到总体的 99% 了，也就是说，我们也可以用 大的前 k 个的奇异值和它所对应的矩阵来近似描述原始矩阵。
SVD 的应用
++图像压缩++：将原始图像的矩阵进行 SVD 分解，只保留前 k 个 大的奇异值，这样的话就保留了图像的主要信息，从而大大减小图像存储的内存需求。这也可用于图像去噪，因为小的奇异值一般对应着噪声。
++PCA 降维++：数据降维。在损失信息较小的情况下，降低数据存储空间，提高后续的机器学习算法速度。同时还能够把真正有用的信息和特征提取出来，便于我们进行分析。
4. 正定矩阵是什么？
判断方法
求出矩阵的所有特征值，若特征值都是 > 0，则矩阵是正定的。
计算矩阵的各阶顺序主子式，如果各阶顺序主子式都 > 0，则矩阵是正定的。
正定矩阵的应用
每一个二次型都唯一对应一个对称矩阵 A，只要 A 是正定的，那么这个函数的二阶导就是正定的，这就可以得出 f(x) 是一个凸函数，意味着 f(x) 的极值就是极小值，并且是全局的 小
值。这个在优化问题、机器学习是非常有用的性质，它可以避免我们得到了驻点，但不是全局小值的情况。
如果 A 是半正定的，那么 小值就不唯一；如果 A 是不定的，没有 小值。所以说当 A 不是正定的情况下， 问题就会复杂一些，所以我们希望这个A是正定的，此时 小化 f(x) 的值就等价于求解一个线性方程组，而后者的理论是非常丰富的。
从系统角度看，如果一个矩阵是正定的，那么我们可以简单理解这个系统拥有全局 小值。而绝大部分问题都可以抽象为解决一个优化问题，如果能证明或者将问题用正定矩阵表示，那么从理论上该问题便拥有全局 优解。而如果拥有全局 优解，我们就能采用很多成熟的方式来求解 优值，这也是机器学习、优化问题 喜欢去研究和解决的情况。
5. 相似矩阵是什么？
相似矩阵的定义
设 A, B 都是 n 阶矩阵，如果存在可逆矩阵 P，使得 P^-1^AP = B，那么就说 B 是 A 的相似矩阵，或者说 A 和 B 是相似的。
相似矩阵的理解
我们知道，每一个矩阵实际上是对应于一种线性变换。
对于同一个线性变换，在不同基下进行描述的不同矩阵，彼此之间称为相似矩阵。
假如说在基 (i, j) 下，向量 x 通过矩阵 A 的线性变换之后得到的新向量为 x'。另一方面，我们也可以先通过一个矩阵 P，把向量 x 换到基 (i', j') 下来表示，这时在新的基下，用来表示上面同一个空间变换的是另一个矩阵 B，它同样也是把向量从x 变换到了 x'，只不过是在另一个坐标系下完成的。因为 终我们还是需要在原坐标系下讨论问题，所以这个时候我们再把向量从
(i', j') 这个基再换回到原来的 (i, j)，也就是左乘一个 P 的逆矩阵。那么这个就是相似矩阵定义的由来。
在实际使用中，可以尝试把 ++普通的非对角矩阵++ 转换为 ++和它相似的对角矩阵++ 来进行处理，从而简化我们的计算过程。
6. 什么是线性相关？什么是线性无关？
在一个向量组中，如果其中存在某个向量可以表示成其他向量的线性组合，那就称该向量组线性相关，反之称为线性无关。
通俗地说就是向量组里如果有向量可以被其他向量表示出来，说明它就是多余的，那么此时就是线性相关。
7. 正交矩阵是什么？
正交矩阵的定义
如果 n 阶方阵 A 满足
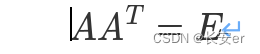我们就称 A 为正交矩阵。
正交矩阵的性质
- 正交矩阵的每一行都是单位行向量，每一列都是单位列向量。
- 正交矩阵的任意两行（列）都是正交的，也就是垂直的。
- 正交矩阵的行列式的值为 1
8.线性空间是什么？
线性空间（Linear Space）是线性代数和数学中的一个概念，通常指的是由向量构成的集合，满足一系列线性性质的数学结构。线性空间也被称为向量空间（Vector Space），它是抽象代数的一部分，用于研究线性关系和线性变换。
9.矩阵如何求逆？
10.两个矩阵A、B，什么情况下AB = BA
如果 A,B互逆，则 AB=BA
在矩阵乘法中，两个矩阵A和B满足A * B = B * A 的情况非常有限。这个等式成立的情况通常是当A和B都是对角矩阵
对角矩阵（ Diagonal Matrix）：
对角矩阵是指只有主对角线上的元素非零，其他元素都是零的矩阵。
如果两个矩阵A和B都是对角矩阵，并且它们的主对角线上的元素相同，那么A * B = B * A。
这是因为对角矩阵的乘法不受矩阵乘法的交换法则影响，只要主对角线上的元素相同，乘法结果是相同的。
11.什么是矩阵的迹，什么是矩阵分解（奇异值分解）
矩阵的迹（ Trace）：
矩阵的迹是指矩阵主对角线上元素的和。如果有一个n x n的矩阵A，其迹记为Tr(A)，计算方式如下：
Tr(A) = a₁₁ + a₂₂ + a₃₃ + ... + aₙₙ
其中，a₁₁、a₂₂、a₃₃等表示矩阵A主对角线上的元素。
矩阵的迹在线性代数中具有多种应用，例如计算矩阵的行列式、计算矩阵的特征值等。它还具有一些有趣的性质，例如Tr(A + B) = Tr(A) + Tr(B)和Tr(AB) = Tr(BA)，其中A和B是可相乘的矩阵。
矩阵分解（ Matrix Decomposition）：
矩阵分解是将一个复杂的矩阵拆分成多个较简单矩阵的过程，这些较简单的矩阵通常具有一些特殊的性质，使得它们更容易分析和处理。常见的矩阵分解方法包括：
- 奇异值分解（ Singular Value Decomposition， SVD）：将一个矩阵分解为三个矩阵的乘积，其中一个是正交矩阵，一个是对角矩阵，另一个是正交转置矩阵。SVD在数据降维、图像处理等领域广泛应用。
- QR分解：将一个矩阵分解为一个正交矩阵Q和一个上三角矩阵R的乘积。QR分解用于线性回归和小二乘问题的求解。
- LU分解：将一个矩阵分解为一个下三角矩阵L和一个上三角矩阵U的乘积。LU分解用于解线性方程组。
- 特征值分解（ Eigenvalue Decomposition）：将一个矩阵分解为一个特征向量矩阵和一个对角矩阵，其中对角矩阵的元素是矩阵的特征值。特征值分解用于寻找矩阵的特征值和特征向量。
这些矩阵分解方法有助于简化复杂矩阵的分析和处理，同时提供了一些重要的数学工具，用于解决线性代数和数值计算中的问题。它们在数据分析、信号处理、机器学习等领域都有广泛的应用。
生活有意思的点就在于未知的某些时刻，你准备去a的时候，可能会遇到b，聊到c，想到d，然后一起去找了e