文章目录
- 视频教程
- [第四章 二维变换与裁剪](#第四章 二维变换与裁剪)
-
- 矩阵基础回顾
- [二维几何变换之 平移](#二维几何变换之 平移)
- [二维几何变换之 比例](#二维几何变换之 比例)
- [二维几何变换之 旋转](#二维几何变换之 旋转)
- [二维几何变换之 反射](#二维几何变换之 反射)
- 复合变换
- [直线裁剪:Cohen-Sutherland 算法](#直线裁剪:Cohen-Sutherland 算法)
- 直线裁剪:中点分割算法
- [直线裁剪:Liang-Barsky 算法](#直线裁剪:Liang-Barsky 算法)
- [多边形裁剪:Sutherland-Hodgman 算法](#多边形裁剪:Sutherland-Hodgman 算法)
视频教程
第四章 二维变换与裁剪
矩阵基础回顾
矩阵是一个由行和列组成的矩形阵列,其中的元素可以是数字、符号或数学表达式。例如,一个 2 × 3 2 \times 3 2×3的矩阵可以表示为:
A = ( a 11 a 12 a 13 a 21 a 22 a 23 ) A = \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \end{pmatrix} A=(a11a21a12a22a13a23)
其中, a i j a_{ij} aij表示矩阵 A A A中第 i i i行第 j j j列的元素。
矩阵的加法:两个大小相同的矩阵 A A A, B B B 相加,结果是另一个矩阵 C C C
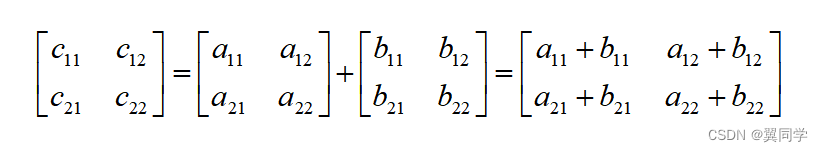
矩阵的乘法:设有两个矩阵 A A A 和 B B B,其中 A A A 是一个 m × n m×n m×n 矩阵, B B B 是一个 n × p n×p n×p矩阵,那么它们的乘积 C C C,即 C = A B C = AB C=AB,是一个 m × p m×p m×p矩阵。
比如我们有两个3行3列的矩阵A和B:
A = ( a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ) A = \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix} A= a11a21a31a12a22a32a13a23a33
和
B = ( b 11 b 12 b 13 b 21 b 22 b 23 b 31 b 32 b 33 ) B = \begin{pmatrix} b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \\ b_{31} & b_{32} & b_{33} \end{pmatrix} B= b11b21b31b12b22b32b13b23b33
它们的乘积C = AB可以表示为:
C = A B = ( a 11 b 11 + a 12 b 21 + a 13 b 31 a 11 b 12 + a 12 b 22 + a 13 b 32 a 11 b 13 + a 12 b 23 + a 13 b 33 a 21 b 11 + a 22 b 21 + a 23 b 31 a 21 b 12 + a 22 b 22 + a 23 b 32 a 21 b 13 + a 22 b 23 + a 23 b 33 a 31 b 11 + a 32 b 21 + a 33 b 31 a 31 b 12 + a 32 b 22 + a 33 b 32 a 31 b 13 + a 32 b 23 + a 33 b 33 ) C = AB = \begin{pmatrix} a_{11}b_{11} + a_{12}b_{21} + a_{13}b_{31} & a_{11}b_{12} + a_{12}b_{22} + a_{13}b_{32} & a_{11}b_{13} + a_{12}b_{23} + a_{13}b_{33} \\ a_{21}b_{11} + a_{22}b_{21} + a_{23}b_{31} & a_{21}b_{12} + a_{22}b_{22} + a_{23}b_{32} & a_{21}b_{13} + a_{22}b_{23} + a_{23}b_{33} \\ a_{31}b_{11} + a_{32}b_{21} + a_{33}b_{31} & a_{31}b_{12} + a_{32}b_{22} + a_{33}b_{32} & a_{31}b_{13} + a_{32}b_{23} + a_{33}b_{33} \end{pmatrix} C=AB= a11b11+a12b21+a13b31a21b11+a22b21+a23b31a31b11+a32b21+a33b31a11b12+a12b22+a13b32a21b12+a22b22+a23b32a31b12+a32b22+a33b32a11b13+a12b23+a13b33a21b13+a22b23+a23b33a31b13+a32b23+a33b33
线性变换是从一个向量空间到另一个向量空间的函数 f f f,满足两个主要条件:加法性(additivity)和齐次性(homogeneity)。具体来说,对于任意向量 u \mathbf{u} u和 v \mathbf{v} v以及任意标量 c c c,线性变换满足:
- 加法性: f ( u + v ) = f ( u ) + f ( v ) f(\mathbf{u} + \mathbf{v}) = f(\mathbf{u}) + f(\mathbf{v}) f(u+v)=f(u)+f(v)
- 齐次性: f ( c u ) = c f ( u ) f(c\mathbf{u}) = cf(\mathbf{u}) f(cu)=cf(u)
线性变换可以通过矩阵乘法来实现。假设有一个线性变换 T T T,它可以用矩阵 M M M表示,那么对于任意向量 x \mathbf{x} x,其变换结果 y \mathbf{y} y可以通过以下方式计算:
y = M x \mathbf{y} = M\mathbf{x} y=Mx
其中, x \mathbf{x} x是一个列向量,表示输入向量, y \mathbf{y} y是变换后的列向量。
二维几何变换之 平移
比如我们有一个点 P ( x , y ) P(x, y) P(x,y),我们想将它平移 Δ x \Delta x Δx 在x轴方向和 Δ y \Delta y Δy 在y轴方向,那么平移后的点 P ′ ( x ′ , y ′ ) P'(x', y') P′(x′,y′) 的坐标可以通过下面的公式计算得到:
x ′ = x + Δ x y ′ = y + Δ y \begin{align*} x' &= x + \Delta x \\ y' &= y + \Delta y \end{align*} x′y′=x+Δx=y+Δy
此时,这个变换可以通过一个特殊的3x3矩阵(变换矩阵 T T T)来表示。为了使用矩阵乘法,我们需要将二维坐标扩展到三维坐标,即 P = [ x , y , 1 ] P = [x, y, 1] P=[x,y,1]。这样,平移变换的矩阵 T T T 和变换后的点 P ′ P' P′ 可以表示为:
T = [ 1 0 0 0 1 0 Δ x Δ y 1 ] T = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ \Delta x & \Delta y & 1 \end{bmatrix} T= 10Δx01Δy001
那么:
P ′ = P ⋅ T = [ x , y , 1 ] ⋅ [ 1 0 0 0 1 0 Δ x Δ y 1 ] = [ x + Δ x , y + Δ y , 1 ] P' = P \cdot T = [x, y, 1] \cdot \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ \Delta x & \Delta y & 1 \end{bmatrix} = [x + \Delta x, y + \Delta y, 1] P′=P⋅T=[x,y,1]⋅ 10Δx01Δy001 =[x+Δx,y+Δy,1]
这样,通过矩阵乘法,我们可以很方便地计算出平移变换后的坐标点。
二维几何变换之 比例
二维坐标的比例变换(或称缩放变换)是另一种基本的几何变换,它根据给定的比例因子在x轴和y轴方向上分别改变点的坐标。
比如我们有一个点 P ( x , y ) P(x, y) P(x,y),想要根据比例因子 α \alpha α 在x轴方向和比例因子 β \beta β 在y轴方向上缩放这个点,那么缩放后的点 P ′ ( x ′ , y ′ ) P'(x', y') P′(x′,y′) 的坐标可以通过下面的公式计算得到:
x ′ = α x y ′ = β y \begin{align*} x' &= \alpha x \\ y' &= \beta y \end{align*} x′y′=αx=βy
为了使用矩阵乘法,我们同样需要将二维坐标扩展到三维坐标,即 P = [ x , y , 1 ] P = [x, y, 1] P=[x,y,1]。这样,比例变换的矩阵 T T T 和变换后的点 P ′ P' P′ 可以表示为:
T = [ α 0 0 0 β 0 0 0 1 ] T = \begin{bmatrix} \alpha & 0 & 0 \\ 0 & \beta & 0 \\ 0 & 0 & 1 \end{bmatrix} T= α000β0001
那么:
P ′ = P ⋅ T = [ x , y , 1 ] ⋅ [ α 0 0 0 β 0 0 0 1 ] = [ α x , β y , 1 ] P' = P \cdot T = [x, y, 1] \cdot \begin{bmatrix} \alpha & 0 & 0 \\ 0 & \beta & 0 \\ 0 & 0 & 1 \end{bmatrix} = [\alpha x, \beta y, 1] P′=P⋅T=[x,y,1]⋅ α000β0001 =[αx,βy,1]
二维几何变换之 旋转
二维坐标的旋转变换可以根据旋转角度在平面内相对于原点对点进行旋转。旋转变换可以是逆时针(正)或顺时针方向(负)。
对于一个点 P ( x , y ) P(x, y) P(x,y),如果我们想将它相对于坐标原点旋转 θ \theta θ 角度,旋转后的点 P ′ ( x ′ , y ′ ) P'(x', y') P′(x′,y′) 的坐标可以通过下面的公式计算得到:
x ′ = x cos ( θ ) − y sin ( θ ) y ′ = x sin ( θ ) + y cos ( θ ) \begin{align*} x' &= x \cos(\theta) - y \sin(\theta) \\ y' &= x \sin(\theta) + y \cos(\theta) \end{align*} x′y′=xcos(θ)−ysin(θ)=xsin(θ)+ycos(θ)
那么变换矩阵 T T T 是:
T = [ cos ( θ ) sin ( θ ) 0 − sin ( θ ) cos ( θ ) 0 0 0 1 ] T = \begin{bmatrix} \cos(\theta) & \sin(\theta) & 0 \\ -\sin(\theta) & \cos(\theta) & 0 \\ 0 & 0 & 1 \end{bmatrix} T= cos(θ)−sin(θ)0sin(θ)cos(θ)0001
那么:
P ′ = P ⋅ T = [ x , y , 1 ] ⋅ [ cos ( θ ) sin ( θ ) 0 − sin ( θ ) cos ( θ ) 0 0 0 1 ] P' = P \cdot T = [x, y, 1] \cdot \begin{bmatrix} \cos(\theta) & \sin(\theta) & 0 \\ -\sin(\theta) & \cos(\theta) & 0 \\ 0 & 0 & 1 \end{bmatrix} P′=P⋅T=[x,y,1]⋅ cos(θ)−sin(θ)0sin(θ)cos(θ)0001
注意,上述式子是 绕原点逆时针旋转 的变换矩阵。如果是顺时针,可以将 θ \theta θ 取为负值,如下所示:
T = [ cos ( − θ ) sin ( − θ ) 0 − sin ( − θ ) cos ( − θ ) 0 0 0 1 ] = [ cos ( θ ) − sin ( θ ) 0 sin ( θ ) cos ( θ ) 0 0 0 1 ] T = \begin{bmatrix} \cos(-\theta) & \sin(-\theta) & 0 \\ -\sin(-\theta) & \cos(-\theta) & 0 \\ 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} \cos(\theta) & -\sin(\theta) & 0 \\ \sin(\theta) & \cos(\theta) & 0 \\ 0 & 0 & 1 \end{bmatrix} T= cos(−θ)−sin(−θ)0sin(−θ)cos(−θ)0001 = cos(θ)sin(θ)0−sin(θ)cos(θ)0001
下面给出基本的三角函数值表格:
| 角度 | sin \sin sin | cos \cos cos | tan \tan tan |
|---|---|---|---|
| 0 ∘ 0^\circ 0∘ | 0 0 0 | 1 1 1 | 0 0 0 |
| 3 0 ∘ 30^\circ 30∘ | 1 2 \frac{1}{2} 21 | 3 2 \frac{\sqrt{3}}{2} 23 | 1 3 \frac{1}{\sqrt{3}} 3 1 |
| 4 5 ∘ 45^\circ 45∘ | 2 2 \frac{\sqrt{2}}{2} 22 | 2 2 \frac{\sqrt{2}}{2} 22 | 1 1 1 |
| 6 0 ∘ 60^\circ 60∘ | 3 2 \frac{\sqrt{3}}{2} 23 | 1 2 \frac{1}{2} 21 | 3 \sqrt{3} 3 |
| 9 0 ∘ 90^\circ 90∘ | 1 1 1 | 0 0 0 | 未定义 |
二维几何变换之 反射
二维坐标的反射变换矩阵,根据反射轴(原点、x轴、y轴)的不同而不同。
当一个点 P ( x , y ) P(x, y) P(x,y) 关于原点 进行反射时,其变换后的点 P ′ ( x ′ , y ′ ) P'(x', y') P′(x′,y′) 的坐标为 ( − x , − y ) (-x, -y) (−x,−y)。对应的变换矩阵 T 原点 T_{原点} T原点 为:
T 原点 = [ − 1 0 0 0 − 1 0 0 0 1 ] T_{原点} = \begin{bmatrix} -1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1 \end{bmatrix} T原点= −1000−10001
当一个点 P ( x , y ) P(x, y) P(x,y) 关于 x x x 轴进行反射时,其变换后的点 P ′ ( x ′ , y ′ ) P'(x', y') P′(x′,y′) 的坐标为 ( x , − y ) (x, -y) (x,−y)。对应的变换矩阵 T x 轴 T_{x轴} Tx轴 为:
T x 轴 = [ 1 0 0 0 − 1 0 0 0 1 ] T_{x轴} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1 \end{bmatrix} Tx轴= 1000−10001
同理,点 P ( x , y ) P(x, y) P(x,y) 关于y轴进行反射时,其变换后的点 P ′ ( x ′ , y ′ ) P'(x', y') P′(x′,y′) 的坐标为 ( − x , y ) (-x, y) (−x,y)。对应的变换矩阵 T y 轴 T_{y轴} Ty轴 为:
T y 轴 = [ − 1 0 0 0 1 0 0 0 1 ] T_{y轴} = \begin{bmatrix} -1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} Ty轴= −100010001
复合变换
当变换方向不与坐标轴重合时,我们可以先根据某个参考点,将其平移到原点位置,然后对平移后的图像进行变换,再根据参考点的位置移回原位。
单选题:图形变换中引入齐次坐标的目的是( C )。
A.便于实现缩放变换
B.便于实现平移变换
C. 统一表示几种基本变换,容易计算
D.便于实现错切变换
单选题:以下关于图形变换的论述不正确的是(D)。
A.平移变换不改变图形大小和形状,只改变图形位置
B.拓扑关系不变的几何变换不改变图形的连接关系和平行关系
C.旋转变换后各图形部分间的线性关系和角度关系不变,变换后直线的长度不变
D.复合变换可以使用一系列连续的简单变换代替, 将这些简单变换的变换矩阵累加起来就得到复合变换矩阵。
备注:是累乘,不是累加。
单选题:实现定点缩放,需要将模型的某个定点先平移到什么位置?(B)
A模型的中心
B坐标系原点
C模型的某个顶点
D以上都不对
单选题:二维图像中,使用下面的变换矩阵变换的结果是(A )。
1 0 0 0 1 0 2 2 1 \] \\begin{bmatrix} 1 \& 0 \& 0 \\\\ 0 \& 1 \& 0 \\\\ 2 \& 2 \& 1 \\end{bmatrix} 102012001 A.图形沿X轴,Y轴各平移2个单位 B.图形放大两倍 C.图形沿X轴,Y轴各平移1个单位,再放大两倍 D.图形不变 *** ** * ** *** 单选题:有二维三角形A(2,5)B(1,1)C(6,3),将其基于B点进行定点缩放,放大两倍,则变换之后A点坐标将变成?(B) A.(4,10) B. (3,9) C. (2,8) D.以上都不对 **解析:** 对于这道题,我们根据 B B B 点作为参考点,首先**平移到坐标原点**,此时变换矩阵为: T 1 = \[ 1 0 0 0 1 0 − 1 − 1 1 \] T_1 = \\begin{bmatrix} 1 \& 0 \& 0 \\\\ 0 \& 1 \& 0 \\\\ -1 \& -1 \& 1 \\end{bmatrix} T1= 10−101−1001 然后将根据坐标原点放大两倍,此时变换矩阵为: T 2 = \[ 2 0 0 0 2 0 0 0 1 \] T_2 = \\begin{bmatrix} 2 \& 0 \& 0 \\\\ 0 \& 2 \& 0 \\\\ 0 \& 0 \& 1 \\end{bmatrix} T2= 200020001 最后再平移回去: T 3 = \[ 1 0 0 0 1 0 1 1 1 \] T_3 = \\begin{bmatrix} 1 \& 0 \& 0 \\\\ 0 \& 1 \& 0 \\\\ 1 \& 1 \& 1 \\end{bmatrix} T3= 101011001 由于A的坐标为(2,5),则设坐标A的齐次矩阵表示为: P = \[ 2 5 1 \] P = \\begin{bmatrix} 2 \& 5 \& 1 \\\\ \\end{bmatrix} P=\[251
代入以下公式,计算即可:
P ′ = P ⋅ T 1 ⋅ T 2 ⋅ T 3 = [ 3 , 9 , 1 ] P' = P \cdot T_1 \cdot T_2 \cdot T_3 = [3, 9, 1] P′=P⋅T1⋅T2⋅T3=[3,9,1]
因此答案为(3, 9)。
单选题:有二维三角形A(2,5)B(1,1)C(6,3),将其进行逆时针旋转90度,则旋转之后A点坐标将变成?(A)
A(-5,2)
B(5,2)
C.(5,-2)
D(-5,-2)
解析:
由于A的坐标为(2,5),则设坐标A的齐次矩阵表示为:
P = [ 2 5 1 ] P = \begin{bmatrix} 2 & 5 & 1 \\ \end{bmatrix} P=[251]
代入以下公式,计算即可:
P ′ = [ 2 5 1 ] ⋅ [ cos ( 9 0 ∘ ) sin ( 9 0 ∘ ) 0 − sin ( 9 0 ∘ ) cos ( 9 0 ∘ ) 0 0 0 1 ] = [ − 5 , 2 , 1 ] P' = \begin{bmatrix} 2 & 5 & 1 \\ \end{bmatrix} \cdot \begin{bmatrix} \cos(90^\circ) & \sin(90^\circ) & 0 \\ -\sin(90^\circ) & \cos(90^\circ) & 0 \\ 0 & 0 & 1 \end{bmatrix} = [-5, 2, 1] P′=[251]⋅ cos(90∘)−sin(90∘)0sin(90∘)cos(90∘)0001 =[−5,2,1]
因此答案为(-5,2)。
单选题:有二维三角形 A(2,5)B(1,1)C(6,3),将其基于 B点 进行定点逆时针旋转90度,则旋转之后A点坐标将变成?(A)
A.(-3,2)
B.(-4,1)
C.(-3,1)
D.(-3,-2)
解析:
对于这道题,我们根据 B B B 点作为参考点,首先平移到坐标原点,此时变换矩阵为:
T 1 = [ 1 0 0 0 1 0 − 1 − 1 1 ] T_1 = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ -1 & -1 & 1 \end{bmatrix} T1= 10−101−1001
然后将根据坐标原点逆时针旋转 9 0 ∘ 90^\circ 90∘ 角,此时变换矩阵为:
T 2 = [ cos ( 9 0 ∘ ) sin ( 9 0 ∘ ) 0 − sin ( 9 0 ∘ ) cos ( 9 0 ∘ ) 0 0 0 1 ] = [ 0 1 0 − 1 0 0 0 0 1 ] T_2 = \begin{bmatrix} \cos(90^\circ) & \sin(90^\circ) & 0 \\ -\sin(90^\circ) & \cos(90^\circ) & 0 \\ 0 & 0 & 1 \end{bmatrix}= \begin{bmatrix} 0 & 1 & 0 \\ -1 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix} T2= cos(90∘)−sin(90∘)0sin(90∘)cos(90∘)0001 = 0−10100001
最后再平移回去:
T 3 = [ 1 0 0 0 1 0 1 1 1 ] T_3 = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 1 & 1 & 1 \end{bmatrix} T3= 101011001
由于A的坐标为(2,5),则设坐标A的齐次矩阵表示为:
P = [ 2 5 1 ] P = \begin{bmatrix} 2 & 5 & 1 \\ \end{bmatrix} P=[251]
代入以下公式,计算即可:
P ′ = P ⋅ T 1 ⋅ T 2 ⋅ T 3 = [ − 3 , 2 , 1 ] P' = P \cdot T_1 \cdot T_2 \cdot T_3 = [-3, 2, 1] P′=P⋅T1⋅T2⋅T3=[−3,2,1]
因此答案为(-3,2)。
直线裁剪:Cohen-Sutherland 算法
算法思想:将裁剪面所在的平面划分成九个区域:
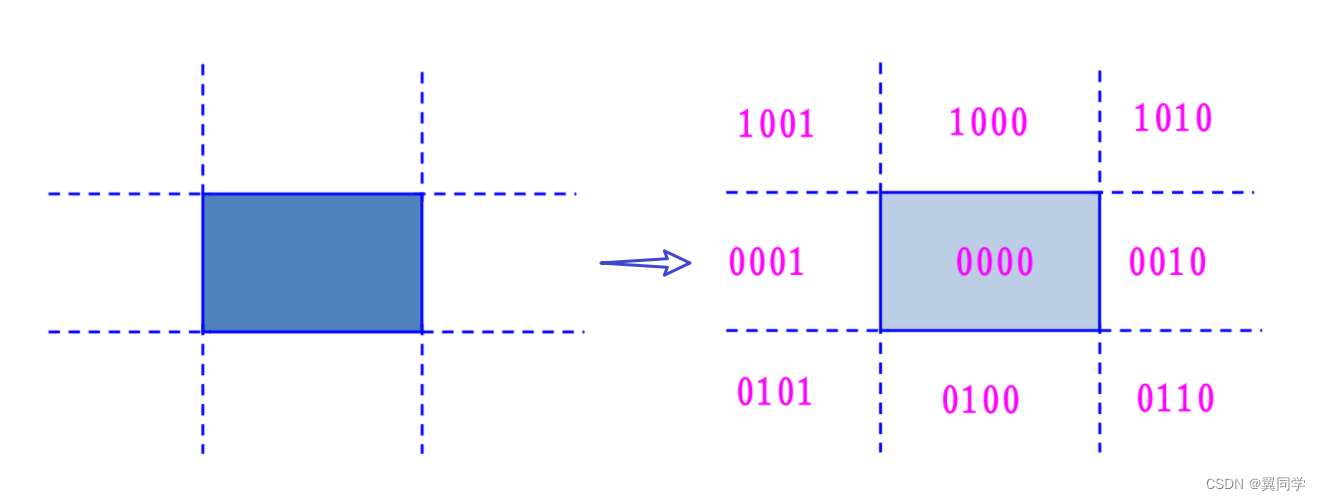
算法的核心思想是:

下面我们来详细看看。首先,这里的 4 位二进制码 R C = C 4 C 3 C 2 C 1 RC = C_4C_3C_2C_1 RC=C4C3C2C1 分别表示:
| C 4 C_4 C4 | C 3 C_3 C3 | C 2 C_2 C2 | C 1 C_1 C1 |
|---|---|---|---|
| 上 | 下 | 右 | 左 |
- 第1位 C 1 C_1 C1:如果该端点位于窗口的左边 ,则 C 1 = 1 C_1 = 1 C1=1,否则 C 1 = 0 C_1 = 0 C1=0。
- 第2位 C 2 C_2 C2:如果该端点位于窗口的右边 ,则 C 2 = 1 C_2 = 1 C2=1,否则 C 2 = 0 C_2 = 0 C2=0。
- 第3位 C 3 C_3 C3:如果该端点位于窗口的下边 ,则 C 3 = 1 C_3 = 1 C3=1,否则 C 3 = 0 C_3 = 0 C3=0。
- 第4位 C 4 C_4 C4:如果该端点位于窗口的上边 ,则 C 4 = 1 C_4 = 1 C4=1,否则 C 4 = 0 C_4 = 0 C4=0。
根据直线两个端点的编码规则进行一些位操作,我们可以清楚直线段所处的位置。
规则一 :如果直线段两个端点的编码 按位或 的结果为0 ,即 R C 0 ∣ R C 1 = 0 RC_{0} | RC_{1} = 0 RC0∣RC1=0,说明线段在裁剪面内部 ,需保留。
大概长这样:
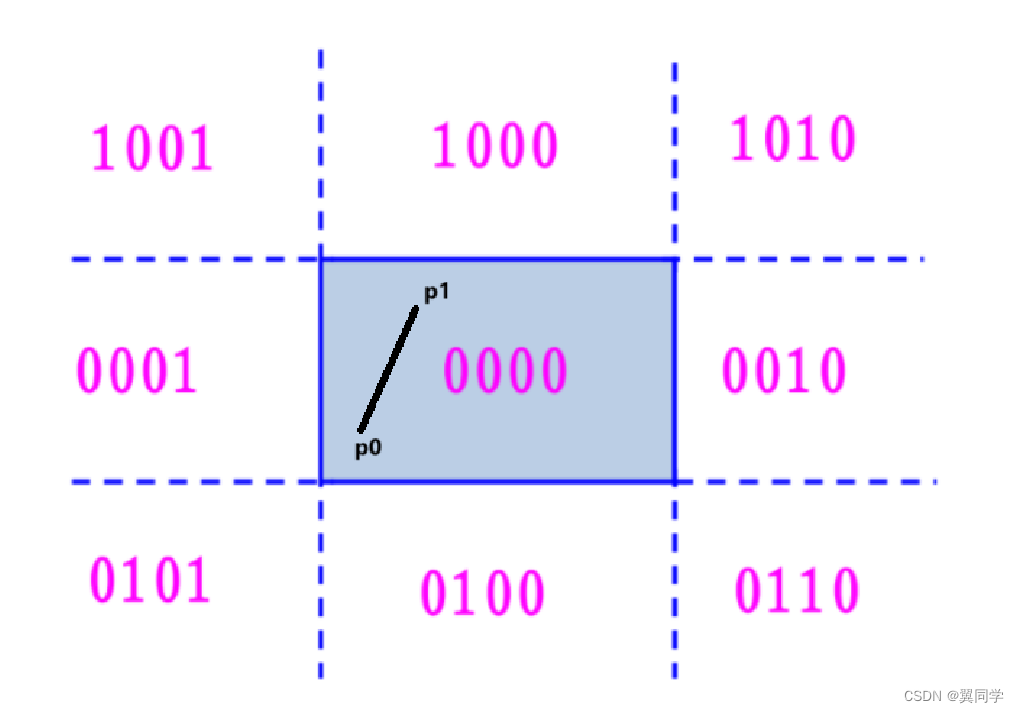
此时:
- P 0 P_0 P0 的编码: R C 0 = 0000 RC_{0} = 0000 RC0=0000,即位于窗口的内部。
- P 1 P_1 P1 的编码: R C 1 = 0000 RC_{1} = 0000 RC1=0000,即位于窗口的内部。
规则二 :如果直线段两个端点的编码 按位并 的结果不等于 0 ,即 R C 0 & R C 1 ≠ 0 RC_{0} \& RC_{1} \neq 0 RC0&RC1=0,说明线段在裁剪面外部 ,需删除。
大概长这样:
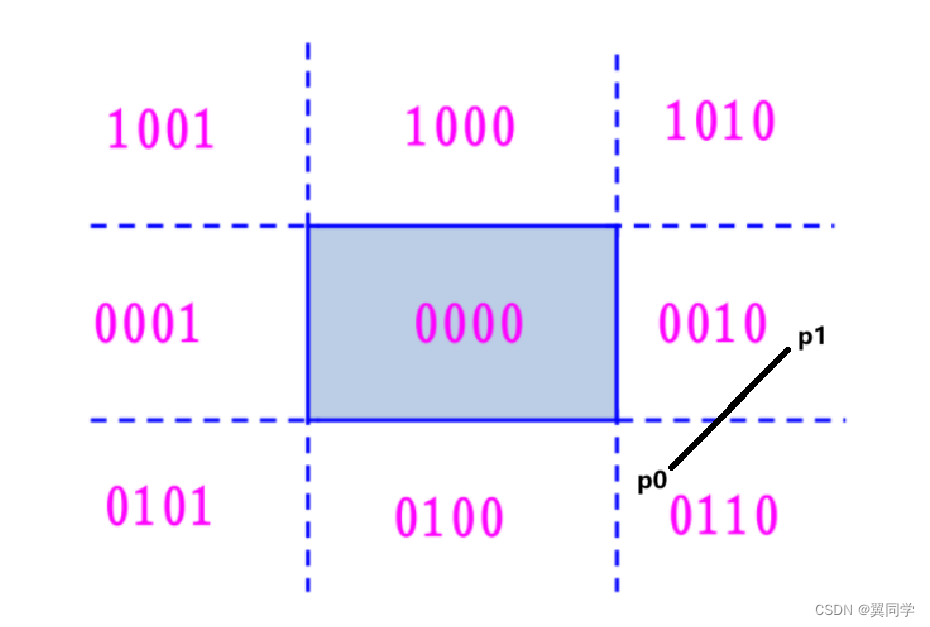
此时:
- P 0 P_0 P0 的编码: R C 0 = 0110 RC_{0} = 0110 RC0=0110,即位于窗口的右下。
- P 1 P_1 P1 的编码: R C 1 = 0010 RC_{1} = 0010 RC1=0010,即位于窗口的右边。
规则三: 如果直线的位置既不满足"规则一"也不满足"规则二" ,那么此时需要与窗口进行 "求交" 运算。
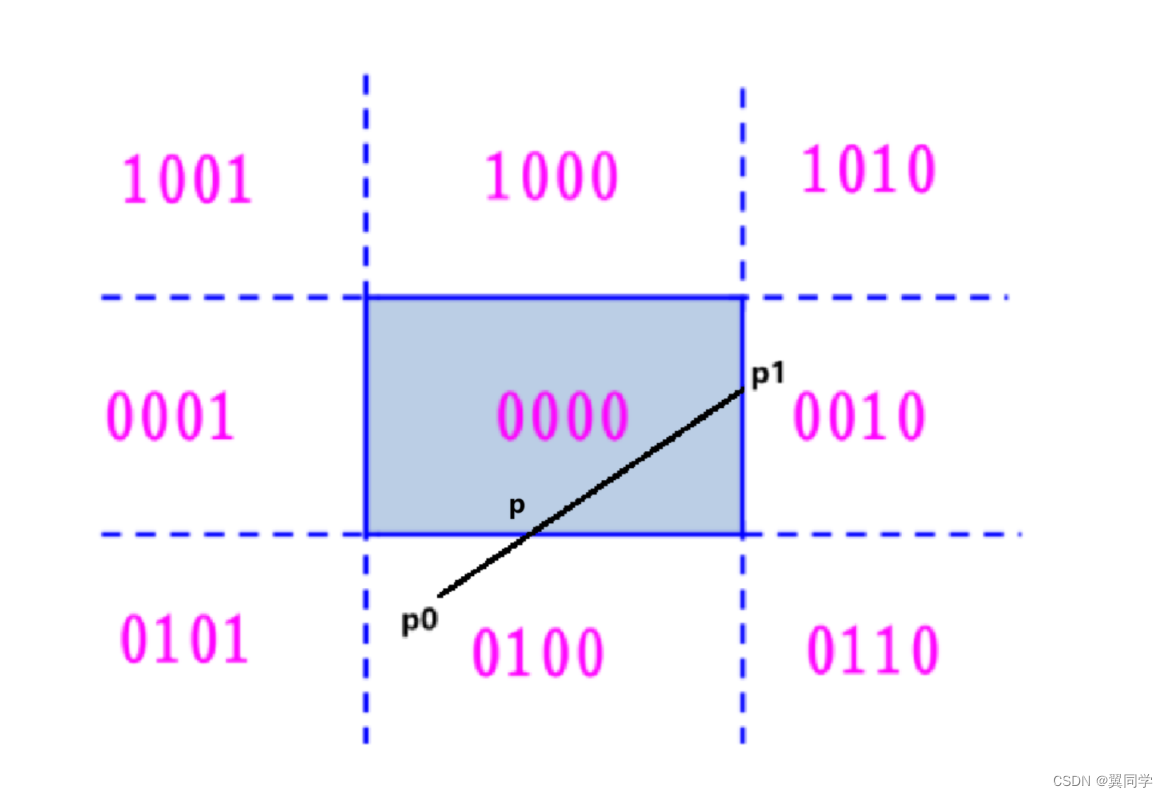
比如有这样的直线:
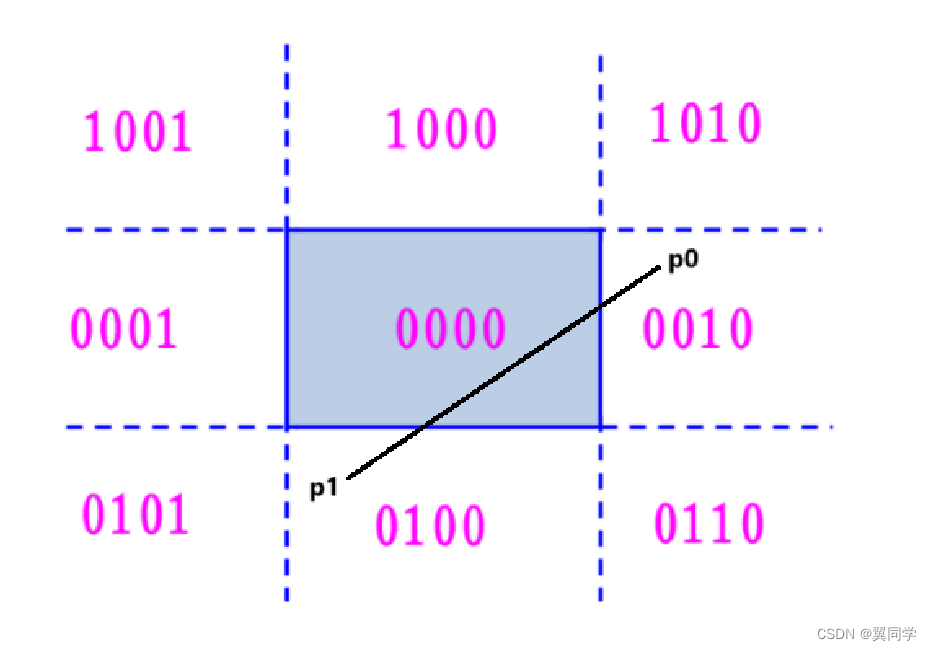
- P 0 P_0 P0 的编码: R C 0 = 0010 RC_{0} = 0010 RC0=0010,即位于窗口的右侧。
- P 1 P_1 P1 的编码: R C 1 = 0100 RC_{1} = 0100 RC1=0100,即位于窗口的下侧。
此时直线段必然与窗口边界(或者窗口边界的延长线相交),现在需要我们来计算一下与窗口的交点。设右边界与 P 0 P 1 P_0P_1 P0P1 的交点为 P P P:
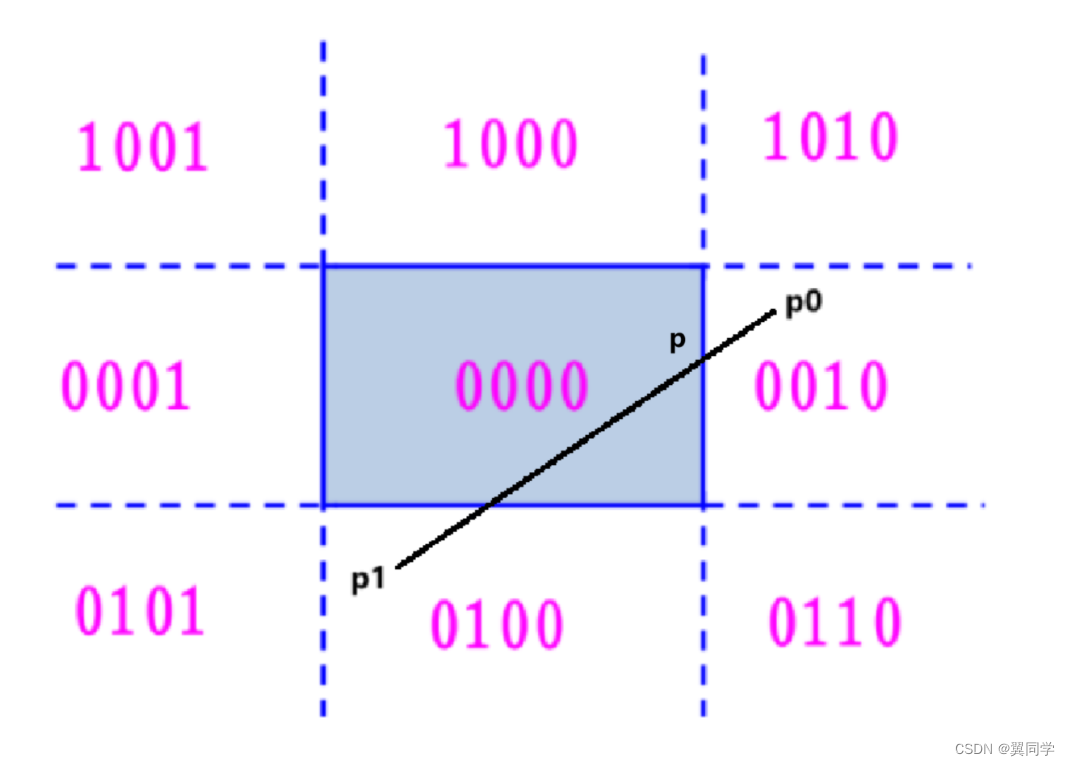
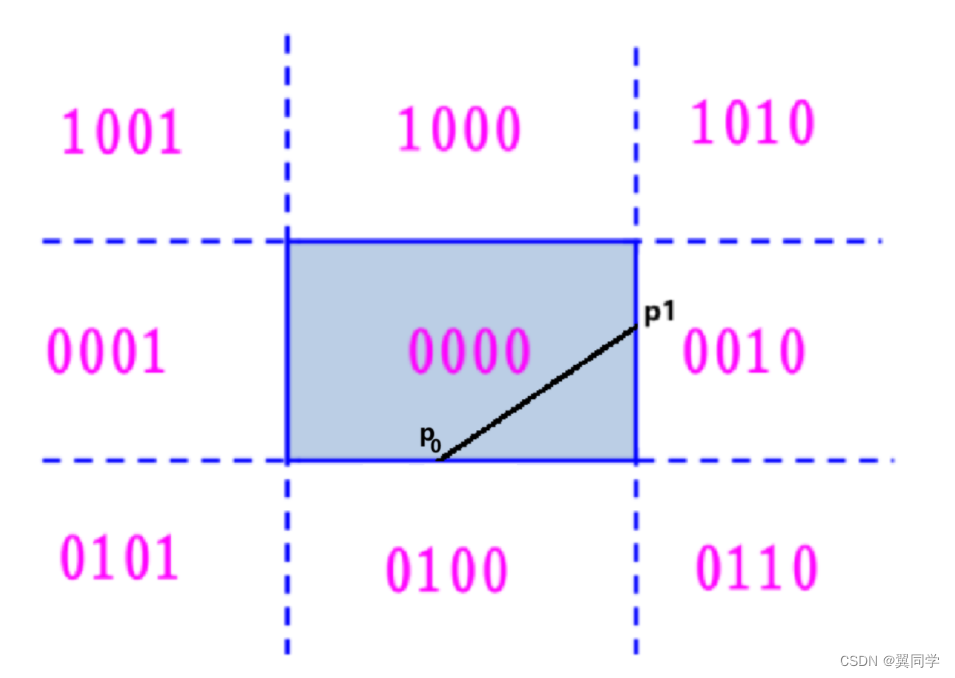
由于直线 P P 0 P P_0 PP0 在窗口的右边,所以删除(舍弃即可)。将 P P P 点的坐标与编码替换为 P 0 P_0 P0 点,并交换 P 0 P 1 P_0P_1 P0P1 的坐标及其编码,使得 P 0 P_0 P0 点总处于窗口之外:
由于直线 P P 0 P P_0 PP0 在窗口的下边,所以删除(舍弃即可)。将 P P P 点的坐标与编码替换为 P 0 P_0 P0 点,如下所示:
单选题:在Cohen-Sutherland直线裁剪算法中,假设两个端点的编码为C1,C2,则判断直线完全保留的判别式是( A )。
A.C1 | C2 == 0
B.C1 & C2 == 0
C.C1 || C2 == 0
D.C1 && C2 == 0
单选题:在Cohen-Sutherland直线裁剪算法中,假设两个端点的编码为C1,C2,则判断直线完全去除的判别式是( B )。
A C1 | C2 == 0
B C1 & C2 != 0
C C1 || C2 == 0
D C1 && C2 == 0
大题:设有如图所示的剪裁窗口和线段 P 1 P 2 P_1P_2 P1P2,试用 Cohen-Sutherland 线段剪裁算法写出图中各个区域的区域码,并详细叙述对直线 P 1 P 2 P_1P_2 P1P2 的剪裁过程。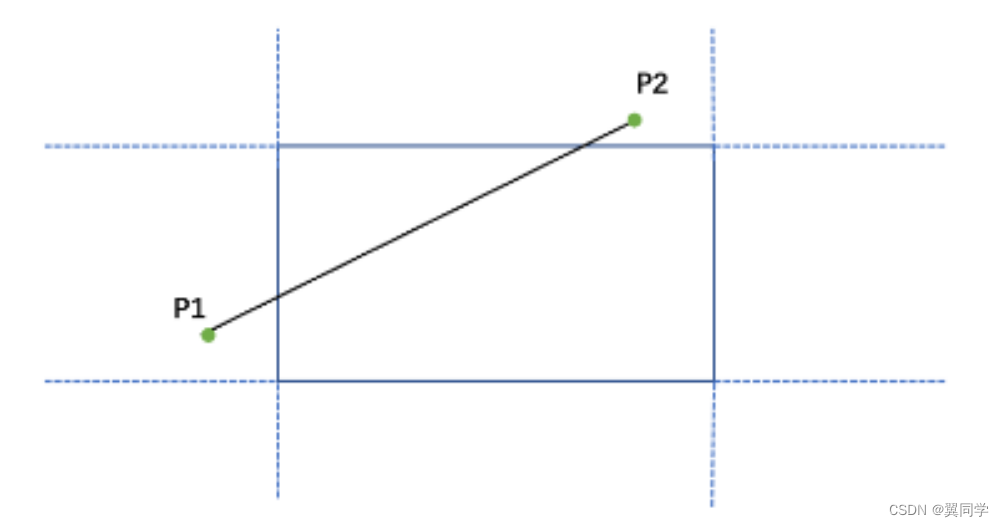
答:
裁剪过程如下:
- 首先,计算区域码:
- P 1 P_1 P1的区域码 C 1 C_1 C1 为 0001 0001 0001
- P 2 P_2 P2的区域码 C 2 C_2 C2 为 1000 1000 1000
- 区域测试 1:
C1 | C2 = 1001 != 0000,证明不完全在裁剪面内部。 - 区域测试 2:
C1 & C2 = 0000,证明不在裁剪面外部,需要进一步求交点。 C1 & 0001 != 0、C1 & 0010 == 0、C1 & 0100 != 0、C1 & 1000 == 0- 解方程组,求出交点 P P P
- P 1 = P P_1 = P P1=P
- 交换 P 1 P_1 P1, P 2 P_2 P2 转 1.
直线裁剪:中点分割算法
核心思路:前几步和 Cohen-Sutherland 算法一样,但是在求交点时,通过不断二分线段并检测与窗口边界的交点来确定线段的可见部分。
算法步骤如下:
- 对线段两端点P1、P2进行编码得到C1、C2。
- 判断线段可见性:
- 若 C 1 = C 2 = 0 C1=C2=0 C1=C2=0 ,线段完全在窗口内,保留。
- 若 C 1 & C 2 ≠ 0 C1 \& C2 ≠0 C1&C2=0 ,线段完全在窗口外,舍弃。
- 否则,需要求交点。
- 求交点过程(核心) :
- 确保窗外端点为P1,若不是则交换P1、P2。
- 保留端点P2到暂存器。
- 对P1重新编码得C1。
- 使用中点公式求中点P,并编码得C。
- 根据中点分割法规则调整P1或P2位置:
- 若P1与P同侧(C1&C!=0),移动P1至P;
- 否则,移动P2至P。
- 重复上述过程,直至P1与P2足够接近,视为找到交点,然后从暂存器取出P2原始值,继续流程。
此算法通过逐步逼近的方式,有效地找到线段与窗口边界的交点,从而确定线段的可见部分。
单选题:中点分割法求交点的规则,当线段P1P2求出中点P后,如果P1与P不同侧,移动P2点,P1与P不同侧的表达式为:( ),其中,C1,C,C2分别是P1,P,P2点的区域编码。(D)
A.(C1&& C)!=0
B.(C1| C)!=0
C.(C1&& C)==0
D.(C1& C)==0
直线裁剪:Liang-Barsky 算法
L i a n g − B a r s k y Liang-Barsky Liang−Barsky 算法是一种基于直线参数方程的裁剪算法,它将二维裁剪问题转化为一维裁剪问题,通过计算直线与裁剪窗口边界的交点来确定直线段在裁剪窗口内的可见部分。
设直线起点为 P 0 ( x 0 , y 0 ) P_0(x_0, y_0) P0(x0,y0),终点为 P 1 ( x 1 , y 1 ) P_1(x_1, y_1) P1(x1,y1),则直线参数方程为:
P = P 0 + t ( P 1 − P 0 ) P = P_0 + t(P_1 - P_0) P=P0+t(P1−P0)
展开式为:
{ x = x 0 + t ( x 1 − x 0 ) y = y 0 + t ( y 1 − y 0 ) , 0 ≤ t ≤ 1 \begin{cases} x = x_0 + t (x_1 - x_0) \\ y = y_0 + t(y_1 - y_0) & , ~~~ 0\leq t \leq 1 \end{cases} {x=x0+t(x1−x0)y=y0+t(y1−y0), 0≤t≤1
设裁剪窗口的坐标为 ( w x l , w y t ) (wxl, wyt) (wxl,wyt) 和 ( w x r , w y b ) (wxr, wyb) (wxr,wyb),则直线段的裁剪条件可以表示为一组不等式,将直线段与窗口边界的相交问题转化为参数 t t t 的一维裁剪问题。
通过定义 u n u_n un 和 v n v_n vn 来表示直线段与裁剪窗口边界的关系,其中 n = 1 , 2 , 3 , 4 n=1,2,3,4 n=1,2,3,4 分别代表窗口的左、右、下、上边界。
裁剪条件可以统一表示为:
t ⋅ u n ≤ v n t \cdot u_n \leq v_n t⋅un≤vn
裁剪窗口的每条边界线将平面分为两个区域:可见侧 和不可见侧 。直线段从可见侧延伸到不可见侧或反之,通过计算 t m i n t_{min} tmin 和 t m a x t_{max} tmax 来确定直线段在裁剪窗口内的可见部分。
L i a n g − B a r s k y Liang-Barsky Liang−Barsky 算法的思路就是:
- 对于直线段的起点 :使用原来的起点 t = 0 t=0 t=0 和由外到内穿过裁剪框的交点判断,取其最大值;
- 对于直线段的终点,使用原来的终点和由内到外穿过裁剪框的交点判断,取其最小值。
直线段位于窗口内的参数条件是: t m a x ≤ t m i n t_{max} \leq t_{min} tmax≤tmin
注意:
- 对于垂直直线段( Δ x = 0 \Delta x = 0 Δx=0),需要特别判断其是否在窗口的左右边界之内。
- 对于水平直线段( Δ y = 0 \Delta y = 0 Δy=0),需要判断其是否在窗口的上下边界之内。
单选题:Liang-Barsky算法裁剪直线段时,对于直线段的起点,使用原来的起点t=0和由外到内穿过裁剪框的交点(入点)判断,取其最大值;对于直线段的终点,使用原来的终点和由内到外穿过裁剪框的交点(出点)判断,取其最小值。直线段位于窗口内的参数条件是 ( C ):
A. t m a x t_{max} tmax >= t m i n t_{min} tmin
B. t m a x t_{max} tmax > t m i n t_{min} tmin
C. t m a x t_{max} tmax <= t m i n t_{min} tmin
D. t m a x t_{max} tmax = t m i n t_{min} tmin
填空题:使用Liang-barsky直线裁剪算法裁剪下面的直线,回答下面的问题:
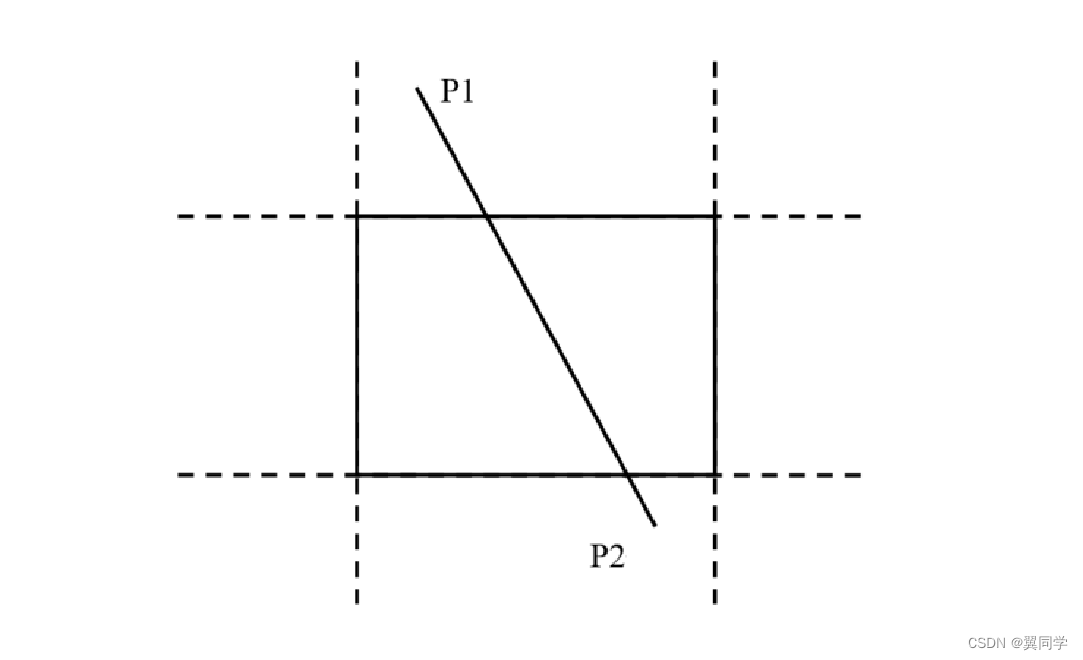
问题一:假设P1点为起点,P2点为终点,直线的方向从P1-->P2。则直线和上裁剪边的交点是【 ____ 】(填 出点 或者 入点),直线和右裁剪边的交点是【 ____ 】(填 出点 或者 入点)。
问题二:假设 t m a x = m a x ( 0 , t 入 ) t_{max} = max ( ~0, t_{入}) tmax=max( 0,t入) 、 t m i n = m i n ( 1 , t 出 ) t_{min} = min ( ~ 1, t_{出}) tmin=min( 1,t出)。则满足【 ____ 】条件,直线部分在窗口内。
答案:
- 【入点】、【出点】
- 【 t m a x ≤ t m i n t_{max} \leq t_{min} tmax≤tmin】
多边形裁剪:Sutherland-Hodgman 算法
Sutherland-Hodgman 裁剪算法又称为逐边裁剪算法,基本思想是用裁剪窗口的 4 条边依次对多边形进行裁剪。窗口边界的裁剪顺序无关紧要,这里采用 左、右、下、上 的顺序。
多边形裁剪算法的输出结果为裁剪后的多边形顶点序列。
在算法的每一步中,仅考虑窗口的一条边以及延长线构成的裁剪线,该线把平面分为两部分:
- 一部分包含窗口,称为可见侧;
- 另一部分落在窗口之外,称为不可见侧。
对于裁剪窗口的每一条边,多边形的任一顶点只有两种相对位置关系,即位于裁剪窗口的外侧(不可见侧)或内侧(可见侧),共有4种情形:
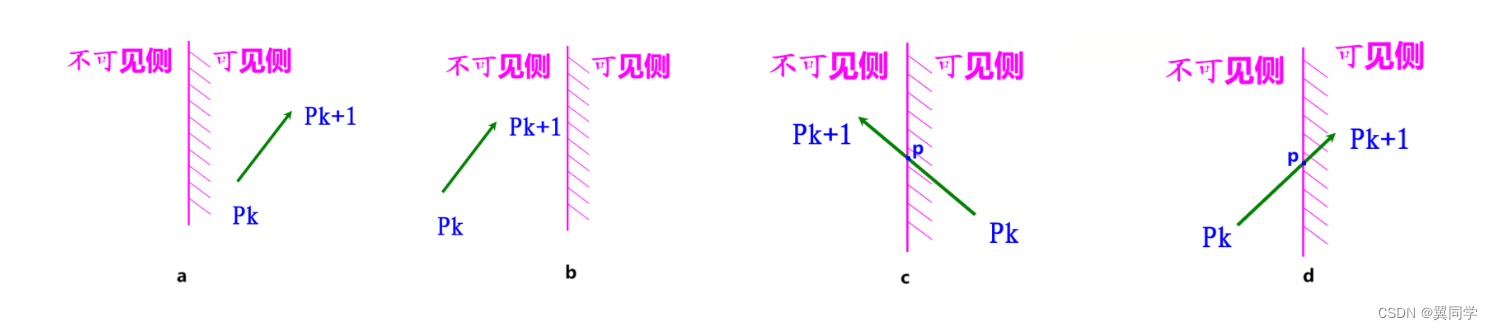
设边的起点为 P k P_k Pk,终点为 P k + 1 P_{k+1} Pk+1,边与裁剪窗口的交点为 P P P ,则有以下四种情况:
- 图 ( a ) :将 P k P_k Pk 加入到输出列表中。
- 图 ( b ):输出列表中不加入任何顶点。
- 图 ( c ) :将 P P P 和 P k P_k Pk 加入到输出列表中。
- 图 ( d ) :将 P P P 加入到输出列表中。
每次处理后,输出一个顶点序列,作为下一次裁剪的输入。通过对多边形的每条边依次进行这样的裁剪处理,最终得到的顶点序列即为多边形关于矩形窗口裁剪后的结果。
单选题:在多边形的逐边裁剪法中,对于某条多边形的边(方向为从端点 P k P_k Pk 到端点 P k + 1 P_{k+1} Pk+1)与某条裁剪线(窗口的某一边)的比较结果共有以下四种情况,分别需输出一些顶点。请问哪种情况下输出的顶点是错误的? ( C ) (C) (C)
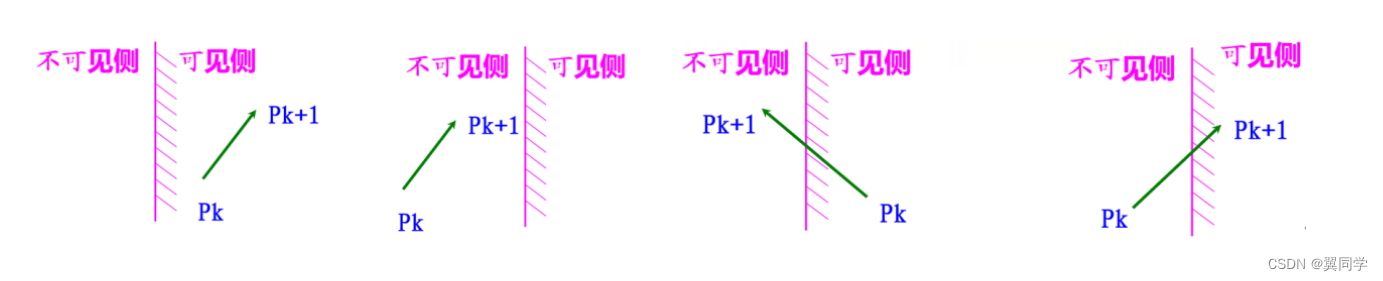
A、 P k P_k Pk 和 P k + 1 P_{k+1} Pk+1 均在可见的一侧,则 P k + 1 P_{k+1} Pk+1。
B、 P P P 和 P k + 1 P_{k+1} Pk+1 均在不可见的一侧,则输出 0 0 0 个顶点。
C、 P k P_k Pk 在可见一侧, P k + 1 P_{k+1} Pk+1 在不可见一侧,则输出线段 P k P k + 1 P_kP_{k+1} PkPk+1 与裁剪边的交点。
D、 P k P_k Pk 在不可见的一侧, P k + 1 P_{k+1} Pk+1 在可见的一侧,则输出线段 P k P k + 1 P_kP_{k+1} PkPk+1 与裁剪线的交点。