矩阵置零解题

STARSpace88882024-07-01 18:14

给定一个 mxn 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用原地算法**。**

示例 1：

复制代码

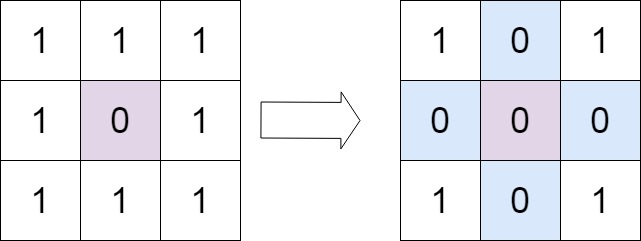
输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出：[[1,0,1],[0,0,0],[1,0,1]]

示例 2：

复制代码

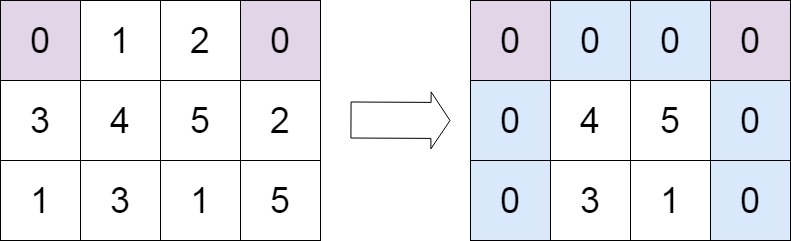
输入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出：[[0,0,0,0],[0,4,5,0],[0,3,1,0]]

解题思路

方法一：创建m*n的数据记录哪一个位置是0，空间复杂度O(m*n)

方法二：找到为0的位置，将对应的第一列/第一行的值设置为0，第一行会有问题，设置一个标记，若第一行出现0，将标记设置为true，在转化

解题

按照解题思路写代码即可，代码附上

java 复制代码

class Solution {
    public void setZeroes(int[][] matrix) {
        boolean flag = false;    //标记
        int row = matrix.length;
        int col = matrix[0].length;
        for (int i = 0; i < row; i++) {
            if (matrix[i][0] == 0) flag = true;
            for (int j = 1; j < col; j++) {
                if (matrix[i][j] == 0) {
                    matrix[i][0] = matrix[0][j] = 0;
                }
            }
        }
        //将第一列和第一行值为0的整个设置为0
        for (int i = row - 1; i >= 0; i--) {
            for (int j = col - 1; j >= 1; j--) {
                if (matrix[i][0] == 0 || matrix[0][j] == 0) {
                    matrix[i][j] = 0;
                }
            }
            if (flag) matrix[i][0] = 0;
        }
    }
}